16. Определение угла между прямой и плоскостью. Вывод формулы вычисления синуса угла между прямой и плоскостью.
УГОЛ МЕЖДУ ПРЯМОЙ И ПЛОСКОСТЬЮ.
Углом между прямой и плоскостью будем называть угол, образованный прямой и её проекцией наплоскость. Пусть прямаяи плоскость заданы уравнениями
Р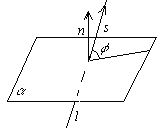
ассмотрим
векторы
и
.
Если угол между ними острый, то он будет
,
где φ – угол между прямой и плоскостью.
Тогда
.
Если
угол между векторами
и
тупой,
то он равен
.
Следовательно
.
Поэтому в любом случае
.
Вспомнив формулу вычисления косинуса
угла между векторами, получим
.
Условие
перпендикулярности прямой и плоскости.
Прямая и плоскость перпендикулярны
тогда и только тогда, когда направляющий
вектор прямой
и
нормальный вектор
плоскости
коллинеарны, т.е.
.
Условие параллельности прямой и плоскости. Прямая и плоскость параллельны тогда и только тогда, когда векторы и перпендикулярны.
17. Вычисление координат точки пересечения прямой с плоскостью.
Постановка задачи.
Найти точку пересечения прямо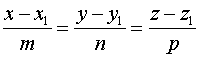й
и
плоскости
.
План решения.
1. Находим параметрические уравнения прямой. Для этого полагаем
,
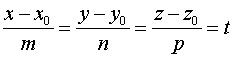откуда получаем
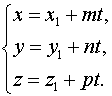
2. Подставляя эти выражения
для
в
уравнение плоскости и решая его
относительно
,
находим значение параметра
,
при котором происходит пересечение
прямой и плоскости.
3. Найденное значение
подставляем
в параметрические уравнения прямой и
получаем искомые координаты точки
пересечения:
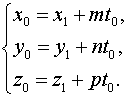
18. Определение расстояния от точки до плоскости. Вывод формулы вычисления расстояния от точки до плоскости.
Расстояние
от точки до плоскости --- это наименьшее
из расстояний между этой точкой и точками
плоскости. Известно, что расстояние от
точки до плоскости равно длине
перпендикуляра, опущенного из этой
точки на плоскость. Если плоскость
задана уравнением
,
то расстояние
от
точки
до
этой плоскости можно вычислить по
формуле
.
19. Уравнение сферы. Приведение уравнения х2 + у2 + z2 + ах + by + cz + d = 0 к стандартному виду.
Уравнение сферы
(x - x0)2 + (y - y0)2 + (z - z0)2 = R2
где (x0,y0,z0) — координаты центра сферы, R — её радиус.
Параметрическое уравнение сферы с центром в точке (x0,y0,z0) :
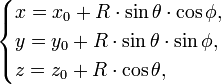
где
и
