1.3.3 Метод дск

Имя метода образовано по начальным буквам фамилий авторов -Девис-Свен-Кэмпей [32]. По своей сути он является усеченным методом Розенброка, в котором отсутствует процедура ортогонализации направлений (1.3.3). Он обладает почти такой же скоростью сходимости, что и метод Розенброка, однако он может вырождаться, т.е. терять какое-либо измерение в n мерном пространстве параметров когда два поисковых направления почти совпадают.

1.3.4 Метод Пауэлла

В методе Пауэлла [14] первые n итераций выполняются также, как и в методе Гаусса-Зейделя. Затем вводится новое направление поиска, совпадающее с направлением полного прохода за предыдущие n итераций. Это направление становится первым, а остальные поисковые направления увеличивают свой номер на единицу. Последнее направление отбрасывается. Алгоритм этого метода следующий.

{{{ Начало алгоритма.

1) Полагаем i=1 и X_i=X_init. Запоминаем начальные направления в матрице P={e_i}, i=1..n.

2) Выбираем поисковое направление P_i из матрицы P и ищем минимум в этом направлении: _i: min_(J(X_i+_iP_i ). Рассчитываем новое приближение вектора поисковых параметров X_i+1=X_i+_iP_i. Увеличиваем i на единицу и если in , то идем в начало пункта 2).

3) Рассчитываем новое направление поиска по формуле:

(1.3.5)

Номера всех направлений в матрице P увеличиваем на единицу:

(1.3.6)

а первым ставим найденное по формуле (1.3.5) P_new .

4) Если |B| , то оптимизацию заканчиваем, иначе полагаем i=1 и переходим к пункту 2).

}}} Конец алгоритма.

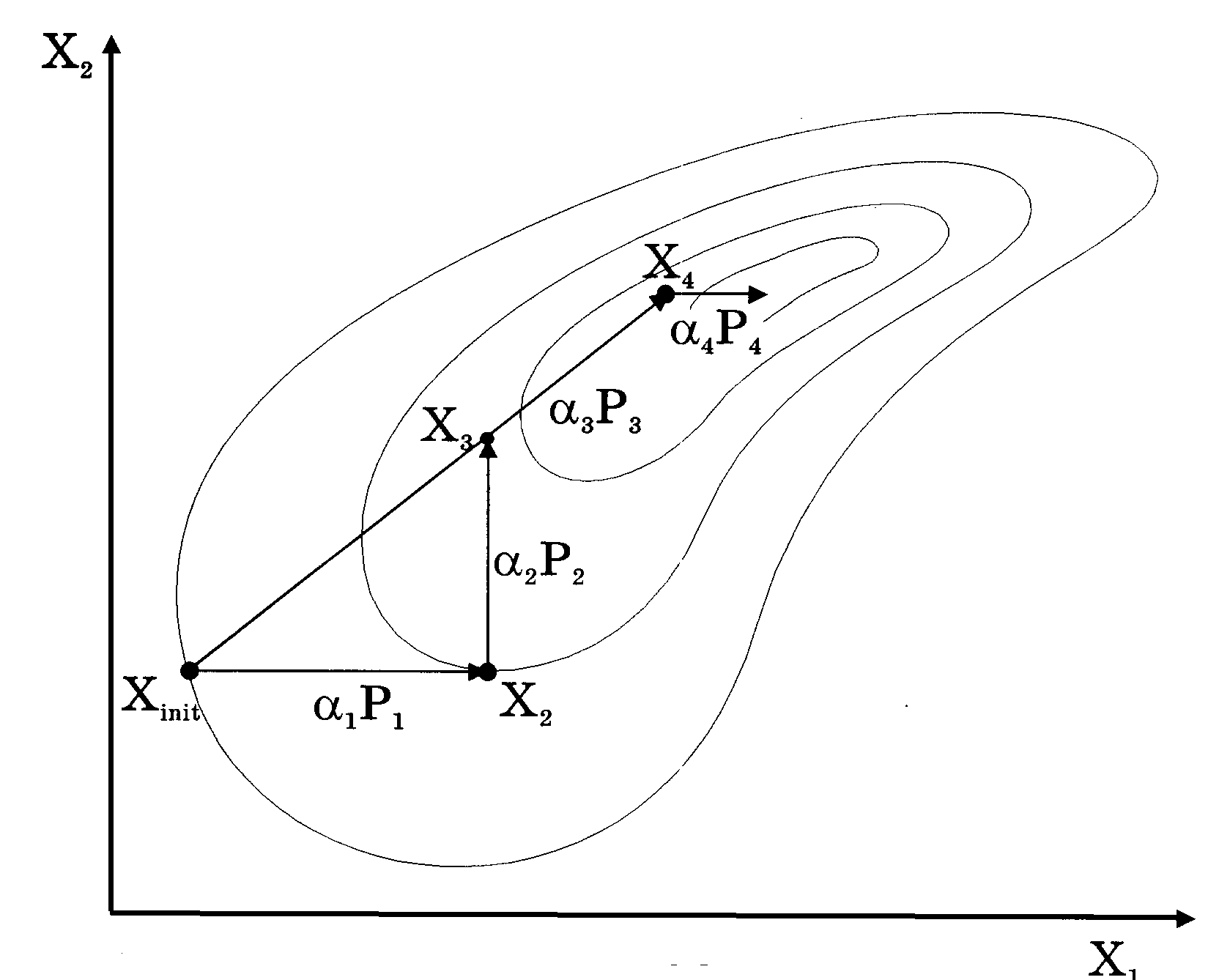
Рис.1.3.3

Поиск минимума методом Пауэлла

Этот метод хорошо работает на функциях, кода главная ось ее прямолинейна, т.к. через n итераций все поисковые направления будут близки к направлению главной оси функции. Однако этот метод может вырождаться и на функциях с криволинейной основной осью не имеет преимуществ перед другими методами. Графически работа метода показана на рис.1.3.3.

1.3.5 Симплексный метод

Под симплексом в n - мерном пространстве понимается многогранник, образованный n+1 вершиной. Например, в двумерном случае симплекс является треугольником, в трехмерном - тетраэдром. Во всех симплекс-методах новое поисковое направление выбирается проходящим через вершину с максимальным значением целевой функции и центр симплекса, который вычисляется без учета этой вершины. В этом направлении делается шаг заданной длины , в новой точке вычисляется значение целевой функции и путем сопоставления этого значения с другими производится или увеличение или уменьшение шага, например, так как это описано в [33]. Некоторые приемы улучшения работы симплекс метода даны в работе Нельдера-Мида [34]. Здесь остановимся на варианте симплекс метода с процедурой поиска минимума в заданном направлении, который свободен от неопределенности некоторых ,ускоряющих, множителей метода Нельдера-Мида.

{{{ Начало алгоритма.

1) Относительно заданного начального приближения вектора поисковых параметров X₀ в заданной сфере радиуса r случайным образом выбираем n+1 вершину симплекса. Запоминаем координаты этих вершин в матрице A={X₁,X₂,..,X_n+1} . Вычисляем значения функций в этих вершинах.

2) Определяем номер вершины симплекса, в которой функция максимальна: j_max: max_j(J(X_j)).

Вычисляем точку центра симплекса:

(1.3.7)

Определяем направление поиска:

P=(X_c-X_jmax)/|P|. (1.3.8)

В заданном направлении P относительно точки X_jmax ищем минимум целевой функции:

₀: min_(J(X_jmax+P) (1.3.9)

и новую точку X_new=X_jmax+₀P вводим в симплекс вместо точки с номером j_max.

3) Если |X_new-X_jmax|, то оптимизацию заканчиваем, иначе переходим к пункту 2).

}}} Конец алгоритма.

Графически работа данного метода в двумерном случае показана на рис.1.3.4.

Рис.1.3.4

Поиск минимума симлексным методом Нельдера-Мида