1.2.2 Методы полиномиальной аппроксимации
Применение методов исключения интервалов требует унимодальности целевой функции в поисковом направлении, т.е. ее монотонности по обе стороны единственной на рассматриваемом интервале точке минимума. При этом функция может иметь разрывы как самой функции так и ее производной. Логическая структура поиска с помощью методов исключения интервалов основана на простом сравнении значений функции в двух точках и не учитывает величину разности между значения функций. В данном разделе рассматриваются методы поиска, которые учитывают относительные изменения целевой функции в опорных точках и поэтому в большинстве случаев оказываются более эффективными, чем методы исключения интервалов. Однако в этом случае необходимо, чтобы целевая функция была достаточно гладкой. Основная идея рассматриваемых методов состоит в аппроксимации целевой функции в заданном направлении полиномом и использования его для оценки точки минимума. Точность оценки можно повысить двумя способами: использованием полиномов более высокого порядка и сокращением интервала аппроксимации. Второй способ более предпочтителен, т.к. построение аппроксимирующего полинома порядка выше третьего довольно сложная процедура, а сократить интервал для унимодальной функции достаточно просто, например, так как это описано разделе 1.2. Простейшим вариантом является квадратичная аппроксимация функции, когда внутри интервала имеется один минимум.
М е т о д к в а д р а т и ч н о й а п п р о к с и м а ц и и
Метод основан на аппроксимации целевой функции по трем опорным точкам - 0, 1, 2 полиномом второй степени:
Y()=a0+a1(-0)+a2 (-0)( -1). (1.2.5)
Для определения коэффициентов a0-2 необходимо решить систему уравнений третьего порядка вида:
(1.2.6)
Решив (1.2.6), получим:
(1.2.7)
Минимуму функции (1.2.5) соответствует точка -
amin=(0+1-a1/a2)/2. (1.2.8)
Окончательно алгоритм метода будет иметь следующий вид.
{{{ Начало алгоритма
1) Запоминаем центральную опорную точку z=1.
2) По заданным трем опорным точкам - 0, 1, 2 и значениям целевой функции - J0, J1, J2 вычисляются по формулам (1.2.7) коэффициенты квадратичного полинома (1.2.6) и по формуле (1.2.8) определяем новую минимальную точку min и рассчитываем в ней значение целевой функции Jmin=J(min).
3) Определяем номер опорной точки, соответствующей максимальному значения целевой функции: im: maxi(Ji). Эту точку исключаем из дальнейшего рассмотрения, а вместо нее вводим вновь найденную минимальную: im=min, Jim=Jmin.
4) Если разница между старым значением z и min меньше заданной точности , т.е. |z-min|<, то поиск заканчивается, иначе запоминается новое значение z=min и переходим к пункту 2).
}}} Конец алгоритма.
1.2.3 Методы с использованием производных
Рассмотренные в предыдущих разделах методы поиска минимума основывались на предположениях об унимодальности и в ряде случаев о непрерывности целевой функции. Если ввести дополнительное требование о непрерывности производных, то эффективность поисковых процедур можно еще повысить. Рассматриваемые в этом разделе алгоритмы можно с успехом использовать в методах оптимизации первого порядка.
М е т о д с е к у щ и х
Этот метод ориентирован на нахождение корня уравнения J()=0 в интервале [1, 2], на концах которого w1=J(1)<0 и w2=J(2)>0. В этом методе используется линейная аппроксимация производной J и алгоритм поиска следующий.
{{{ Начало алгоритма.
1) Запоминается крайняя точка z=1.
2) Из подобия треугольников ( см. рис.1.2.5) определяем следующее приближение стационарной точки по формуле:
(1.2.9)
В этой точке рассчитывается значение производной w3=J(3).
3) Если w3>0, то эта точка берется в качестве новой правой точки: 2=3 , w2=w3, иначе - в качестве левой: 1=3, w1=w3.
4) Если |z-3|<, то поиск минимума окончен, иначе запоминается новое значение z=3 и переходим к пункту 2).
}}} Конец алгоритма.
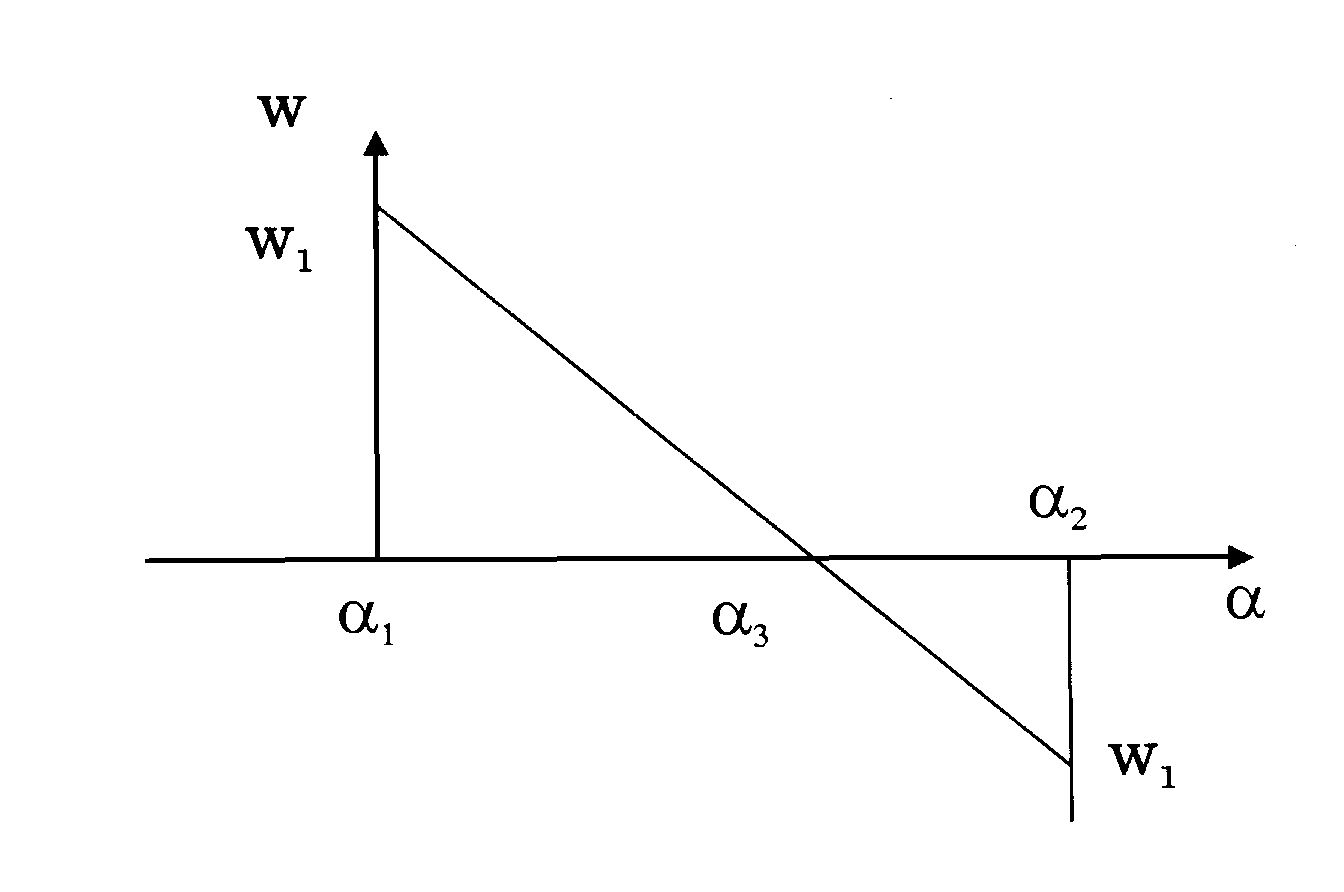
Рис.1.2.5
Алгоритм метода секущих
М е т о д к у б и ч е с к о й а п п р о к с и м а ц и и
Целевая функция в этом методе аппроксимируется полиномом третьей степени. Логическая структура метода аналогична схеме метода квадратичной аппроксимации. Однако в данном методе для аппроксимации используются только две опорные точки 1 и 2 и значения функций и производных в этих точках: J1=J(1), J2=J(2), w1=J(1), w2=J(2). Аппроксимирующий полином можно искать в виде:
Y()=a0+a1(-1)+a2(-1)( -2)+a3(-1)2(-2). (1.2.10)
Коэффициенты a0-3 определяются путем решения следующей системы
линейных уравнений:
(1.2.11)
Приравняв к нулю производную от полинома (1.2.10) получим квадратное уравнение относительно , решение которого определяет минимальную точку кубического полинома и для случая w1<0 имеет вид ( см. [8] ):
min=(2-1)(1-(w2+b-a)/c), (1.2.12)
где a=3(J1-J2)/( 2-1)+w1+w2,
b=(a2-w1w2)1/2,
c=w2-w1+2b.
Алгоритм данного метода может выглядеть следующим образом.
{{{ Начало алгоритма.
1) Запоминаем граничное значение переменной z=1.
2) По формулам (1.2.12) определяем min и рассчитываем в этой точке Jmin=J(min) и wmin=J(min).
3) Если Jmin<J1 и wmin<0 , то производим следующую замену: 1=min, J1=Jmin, w1=wmin, иначе: 2=min, J2=Jmin, w2=wmin.
4) Если |wmin|< или |min-z|< , то поиск заканчивается , иначе полагаем z=min и переходим к пункту 2).
}}} Конец алгоритма.