1.2 Методы одномерного поиска
Поиск минимума вдоль направления P является одномерным поиском относительно параметра в выражении (1.1.2). Одномерный поиск осуществляется в два этапа.
На первом этапе определяется приближенно область параметра [1, 2] в которой предполагается находится минимум целевой функции J(). Строгих методов для этой процедуры нет. Если не вычисляются производные от целевой функции по , то обычный алгоритм заключается в следующем ( см. рис.1.2.1).
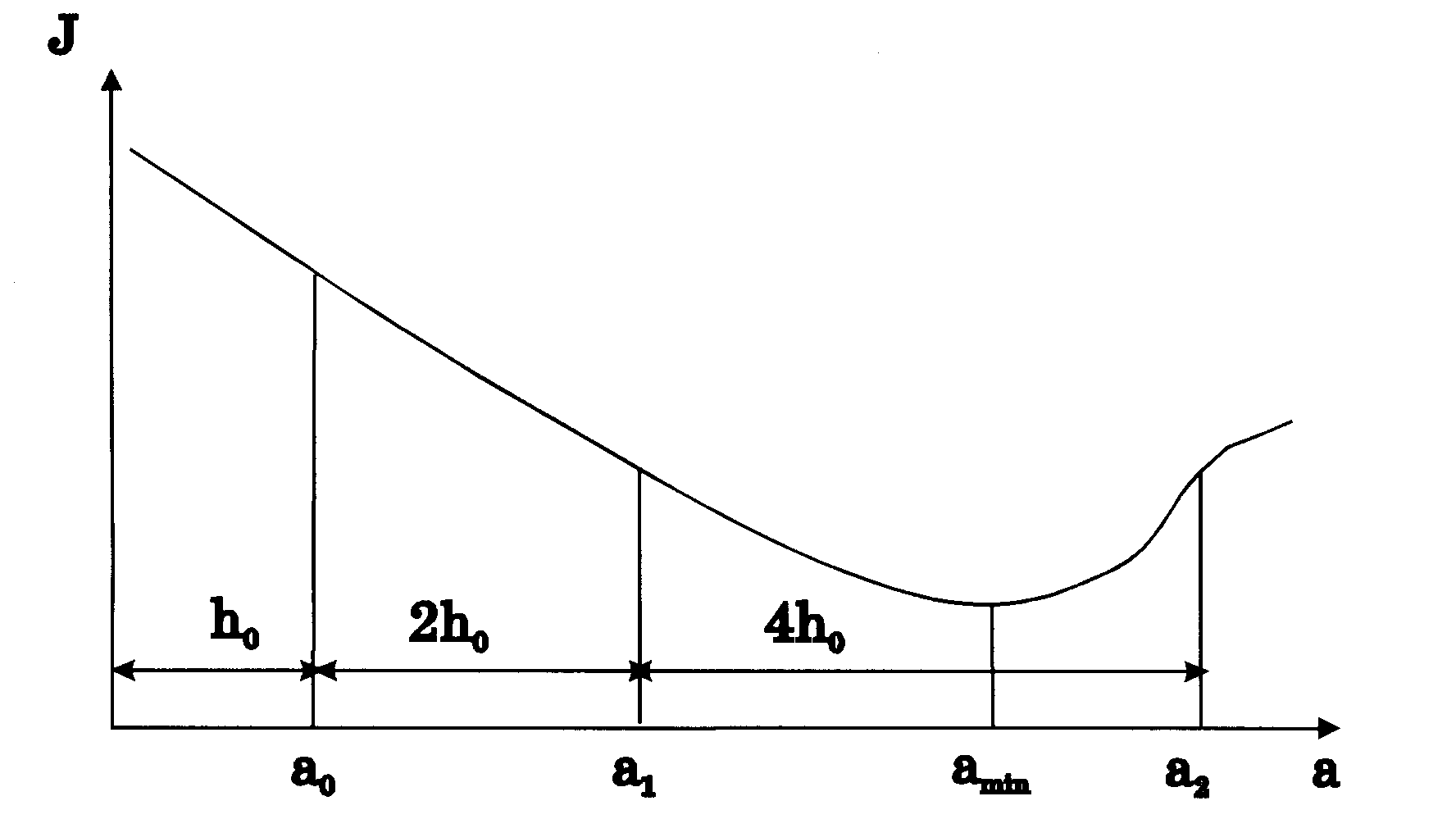
Рис.1.2.1
Алгоритм приближенного определения минимума функции
1) Задаются начальным шагом по - h0 , который определяют экспериментально. Начальное значение полагают равным нулю - =0 и h=h0.
2) Далее запоминаем текущие значения 1= и J1=J(1) и увеличиваем значение на величину h . В новой точке 2=1+h вычисляется значение целевой функции J2=J(2).
Если J2 J1 и h h0 , то
а) шаг h обычно увеличивают вдвое, т.е. h=2h, вводится система пере обозначений вида: 0=1, J0=J1, 1=2, J1=J2, =1 и снова идем на начало пункта 1) до тех пор пока h не превысит начальное значение шага h в 210 раз. Это означает, что в данном направлении минимум отсутствует. Иначе: б) Если h > h0 , то имеется три точки по - 0 ,1 ,2 , заключающие внутри себя точку минимума целевой функции min , и можно в этом случае переходить к методу уточнения местоположения минимума, т.е. к пункту 3), в противном случае начальный шаг делим на четыре - h= h/4 , полагаем 1==0, J1=J(0) и идем к пункту 2). Деление шага h производят до тех пор пока он не станет меньше начального шага h0 в 220 раз. Если он станет меньше, то в данном направлении будем считать минимума нет.
3) Уточняем местоположения минимума целевой функции по - min.
В случае расчета производных от целевой функции по параметру , алгоритм приближенного определения местоположения минимума целевой функции может быть следующим(см. рис.1.2.2).
Рис.1.2.2
Алгоритм приближенного определения минимума функции с использованием производных
1) Зададимся начальным шагом по - h0 , который, например, можно вычислить по формуле:
h=(Jmin-J(0))/(2J(0)), (1.2.1)
где Jmin - предполагаемое минимально возможное значение целевой функции, J(0) - производная от целевой функции по параметру в начальной точке, где =0. В общем случае эта производная вычисляется как
(1.2.2)
т.е. как проекция градиента g(Xk) на поисковое направление Pk. Если эта производная будет положительна, то это означает что в данном направлении минимум отсутствует и следует рассчитать новое поисковое направление Pнов. Начальное значение полагают равным нулю - =0 и h= h0.
2) Далее запоминаем текущие значения 1=, w1=J(1) и J1=J(1) и увеличиваем значение на величину h. В новой точке 2=1+ h вычисляется значение целевой функции J2=J(2) и производная w2=J(2). Если w2<0 и J2<J1, то
а) вводится система пере обозначений 1=2, w1=w2, =1, J1=J2, шаг увеличивают в два раза - h=2 h и идем в начало пункта 1), иначе
б) переходим к пункту 3) - уточнению местоположения минимума.
3) Вызов процедуры уточнения местоположения минимума целевой функции по на отрезке 1 - 2.
На втором этапе одномерного поиска осуществляется уточнение местоположения минимума целевой функции по параметру в заданном интервале и с заданной точностью - .