1.8.1 Конечно-разностный метод

Для поисковых расчетов с постоянно меняющейся математической моделью процессов в приборе проще и надежнее определять производные с помощью конечных разностей. Программа в этом случае содержит только расчет производных и ограничений.

Большое значение при численном определении производных имеет достижении возможно меньшей ошибки в ее расчете, которая будет определяться выбором приращения по параметру.

Производную будем приближенно определять по двухточечной схеме по формуле:

(1.8.1)

Для оценки ошибки расчета производной по формуле (1.8.1) разложим функцию J в ряд Тейлора относительно точки X_k:

J(X_k+)=J(X_k)++²+... (1.8.3)

Здесь

Третий член в разложении (1.8.2) определяет основную ошибку усечения, т.е. ошибку связанную с наличием нелинейной зависимости J от d. Относительная ошибка усечения будет определяться как:

(1.8.3)

Из формулы (1.8.3) следует, что при увеличении  будет увеличиваться и ошибка усечения. С другой стороны посмотрим, что будет происходить при уменьшении шага . Все вещественные величины в ЭВМ хранятся с определенной точностью, которая зависит от длины разрядной сетки отводимой для мантиссы вещественного числа. Поэтому расчет целевой функции J всегда производится с какой-то точностью. Допустим, что

и (1.8.5)

Тогда (1.8.6)

Ошибка сокращения, вызванная неточностью расчета J, определяется как

(1.8.7)

Из (1.8.7) следует, что с уменьшением  ( и одновременным уменьшением ) ошибка сокращения _сок будет возрастать. Это явно противоположно поведению ошибки усечения _ус . Для того, чтобы ни одна из ошибок не доминировала примем компромиссное решение - приравняем эти ошибки и из этого уравнения определим оптимальную длину шага :

|J|-4|J_J|=0, (1.8.8)

или ²²/2+||²-4|J_J|=0. (1.8.9)

Приближенное решение уравнения (1.8.9) дает:

(1.8.10)

Уточнение решения (1.8.10) методом последовательных приближений позволяет получить следующее выражение для оптимальной длины шага :

(1.8.11)

С другой стороны сами поисковые параметры X задаются и хранятся в памяти ЭВМ с конечной точностью, которая в свою очередь влияет на точность расчета производной. Приближенное значение поискового параметра можно представить в виде:

(1.8.12)

Такое представление поискового параметра приводит к следующей погрешности расчета целевой функции в первом приближении :

(1.8.13)

где _JX определяет погрешность расчета целевой функции обусловленную неточностью задания значения поискового параметра X. Поэтому для расчета шага по параметрам значение относительной погрешности расчета целевой функции выбирают как максимальное из двух значений:

(1.8.14)

Если после расчета производной по формуле (1.8.1) не выполняется неравенство (1.8.3), то для уменьшения ошибок усечения следует воспользоваться для расчета производной симметричной двухточечной формулой вида:

(1.8.15)

Это приводит, однако, к увеличению в два раза времени на расчет производной. В этом случае для расчета приращения  следует воспользоваться впрямую разложением (1.8.2), где следует задать приращение целевой функции исходя из заданных значений относительных погрешностей _J и _ в виде:

J=|J(X_k)_j/_|. (1.8.16)

Тогда уравнение для расчета  примет вид:

||²/2+||-|J_J/_|=0, (1.8.17)

откуда значение  определяется как:

(1.8.18)

В формулах (1.8.10), (1.8.11) и (1.8.18) используются диагональные члены матрицы Гессе . При реализации методов с переменной метрикой в памяти ЭВМ хранится только приближение обратной матрицы Гессе - H_k. Для исключения процедуры обращения матрицы можно наряду с пересчетом корректирующей матрицы E_k пересчитывать и диагональные члены матрицы Гессе. Для этого можно воспользоваться формулой Хаусхолдера [36] для обращения матриц:

(1.8.20)

где B - матрица, U и V - произвольные вектора, а  - скаляр.

Тогда для метода Давидона-Флетчера-Пауэлла приближение матрицы Гессе будет иметь вид:

(1.8.21)

а для метода Гольдфарба :

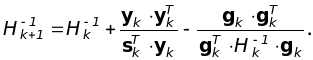(1.8.22)

В итоге алгоритм для расчета производной будет следующим.

{{{ Начало алгоритма.

1) Для заданных значений относительных погрешностей определения целевой функции, производных и поисковых параметров - _J, _ и _x, а также текущих значений J(X_k),  и  определяем максимальную погрешность расчета целевой функции _J^* по формуле (1.8.14).

2) Вычисляем оптимальную величину шага по параметру d по формулам(1.8.10) и (1.8.11).

3) Если 0.5|/| < _J^*/_ , то рассчитываем новое значение производной по формуле (1.8.1), а иначе пересчитываем  по формуле (1.8.18) и рассчитываем производную по формуле (1.8.15).

}}} Конец алгоритма.

1.8.2 АУС-метод

Если процессы в электронном приборе описываются системой обыкновенных дифференциальных уравнений, то расчет производных от целевой функции по искомым параметрам можно осуществить с помощью АУС- метода (Аппроксимация Управления и применение Сопряженной системы уравнений) [10]. Этот метод позволяет существенно ускорить (в ~(n+1)/2 раз) процедуру расчета градиента от целевой функции по поисковым параметрам. Однако он приводит и к существенному усложнению программы (приблизительно в 4 раза возрастает объем программы), замедляется процесс отладки и поиск ошибок. Поэтому АУС-метод следует применять только в случаях, когда разрабатываемая программа будет многократно использоваться для оптимизации электронных приборов по большому числу параметров.

П о с т а н о в к а з а д а ч и

1. Пусть задана математическая модель процесса в электронном приборе в виде системы обыкновенных дифференциальных уравнений:

(1.8.23)

где Y- m- мерный вектор фазовых переменных, t- независимая переменная (например, время или продольная координата), U(X,t)- l- мерный вектор управления процессом (например, распределение по длине прибора магнитостатического поля или профиля волновода), X- n-мерный вектор параметров управления (например, ток, напряжение электронного потока, амплитуда и фаза ВЧ поля в резонаторе, его добротность и расстройка и т.д.), t₀ t  T.

Для уравнения (1.8.23) заданы граничные условия, которые в общем случая могут быть записаны в виде:

(Y(t₀),t₀,Y(T),T,X)=0, (1.8.24)

где  - p-мерный вектор граничных условий ( p  2m+1 ). Если значения t и T определяются из условий (1.8.24) , то мы имеем задачу с подвижными концами (t₀ и T).

Функции управления U(X,t) обычно представляют в виде конечного разложения по системе базисных функций, которые, как правило, образуют полную систему функций и удовлетворяют условиям взаимоортогональности. Например, управления U(X,t) могут иметь вид:

(1.8.25)

где k- длина разложения, A_ij - искомые коэффициенты разложения, которые входят в вектор X, _ij(t)- базисные функции. Базисными функциями могут быть, например, полиномы Чебышева, Лежандра, Эрмита, Лагерра, тригонометрические функции и т.д.

Представления функций управления можно выбрать так, что U(X,t) могут уже заранее удовлетворять определенным физическим ограничениям решаемой задачи, например, ограничениям на максимальную величину управления, условиям непрерывности, как самой функции, так и ее производных, условиям унимодальности и т.д., что заранее позволяет исключить введение дополнительных ограничений на управления.

2. Задана целевая функция или критерий качества в виде:

J=(X,t₀,T,Y(t₀),Y(T)). (1.8.26)

В теории оптимального управления такая функция определяет задачу Майера. Задачу Лагранжа, где определяется интегральный функционал, можно свести к задаче Майера путем введения дополнительной фазовой переменной. Аналогично можно привести более общую задачу Больца, где есть функция вида (1.8.26) и интегральный функционал, к задаче Майера.

Кроме того, будем предполагать, что в какой-то момент времени t' уравнения состояния (1.8.23) будут иметь разрыв первой производной , т.е. для t<t' , где функция переключения (Y,t)>0, уравнение (1.8.23) имеет вид:

(1.8.27)

а для t>t', где функция (Y,t)<0, уравнение (1.8.23) имеет вид:

(1.8.28)

Это приводит к появлению дополнительного условия:

(Y(t'),t')=0. (1.8.29)

В задачах электроники СВЧ такой случай может возникнуть, например, при оседании части электронного потока на трубку дрейфа, когда правая часть уравнения (1.8.23) обращается для таких электронов скачком в ноль.

В с п о м о г а т е л ь н ы й ф у н к ц и о н а л

Для решения задачи условной оптимизации составим согласно методу множителей Лагранжа вспомогательный функционал вида:

(1.8.30)

Здесь введены следующие обозначения:

(1.8.31)

H^ - функция Гамильтона, , , - множители Лагранжа.

Первая вариация функционала будет иметь вид:

Развернув отдельные слагаемые этого выражения, получим:

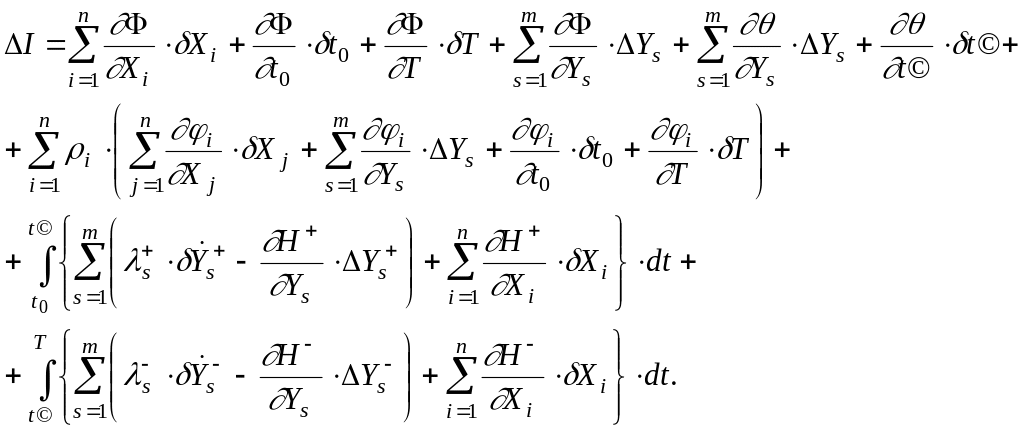(1.8.32)

Проинтегрировав слагаемые 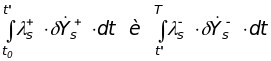по частям, будем иметь следующие выражения:

(1.8.33)

(1.8.34)

В линейном приближении (см. рис.1.8.1) можно записать:

(1.8.35)

Из (1.8.35) можно найти Y^ и подставив их в формулы (1.8.33) и (1.8.34) получим следующее выражение в векторной форме для первой вариации функционала:

(1.8.36)

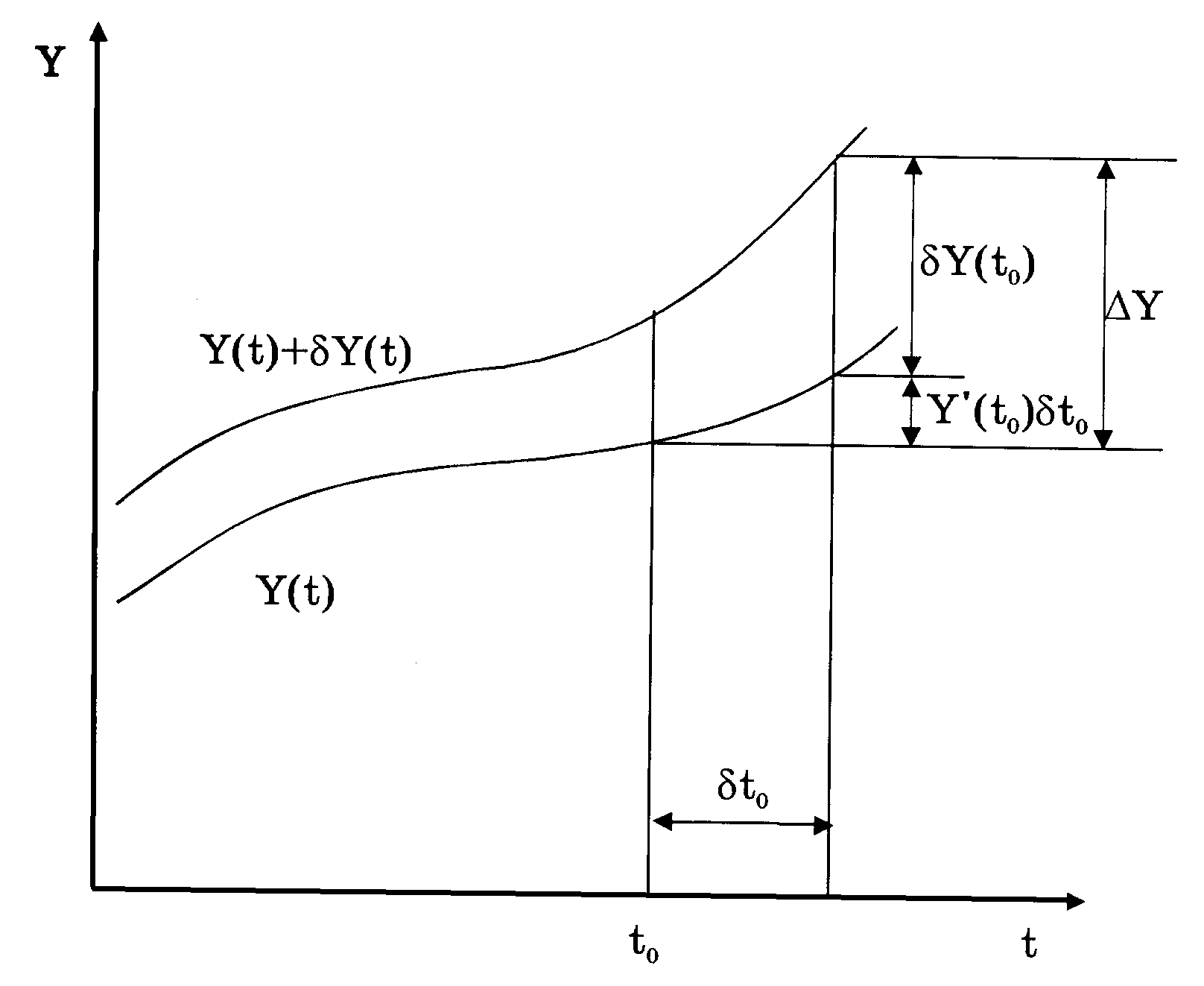
Рис.1.8.1

Определение вариации фазовой переменной

Здесь, верхний индекс «T» означает транспонирование вектора, нижний индекс - частную производную по этому индексу, причем производная по вектору воспринимается как вектор - строка. Например, .

В выражение (1.8.36) входят, кроме первой вариации по X, три типа слагаемых: первые зависят от вариаций концов траекторий сравнения, вторые - от вариаций в точке t=t' и, наконец, третьи содержат интегралы. Все эти группы могут меняться независимо, в них входят неопределенные пока множители Лагранжа - , ,  и мы можем их доопределить приравняв каждую из этих групп нулю. Это позволяет получить следующие равенства:

(1.8.37)

(1.8.38)

(1.8.39)

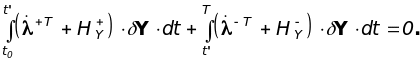(1.8.40)

Рассмотрим последнее из них. Чтобы удовлетворить ему, выберем ^(t) так, чтобы выполнялись уравнения

. (1.8.41)

Вариации Y(t₀), Y(T), t₀ и T связаны соотношениями (1.8.24). Выберем p множителей _i , входящих в функцию (1.8.29) так, чтобы обратились в нуль коэффициенты при p зависимых вариациях из совокупности Y(t₀), Y(T), t₀ и T. Тогда в равенстве (1.8.37) останутся только независимые вариации. Коэффициенты при них должны быть равны нулю. В результате концевые условия будут иметь вид:

(1.8.42)

Входящие в равенство (1.8.39) вариации Y(t') и t' связаны одним условием (1.8.29). Соответствующий множитель Лагранжа  выберем так, чтобы обратить в нуль коэффициент при единственной зависимой вариации. Останется m независимых вариаций, коэффициенты при них должны быть равны нулю в соответствии с соотношением (1.8.39). В результате получим следующие условия Эрдманна-Вейерштрасса:

(1.8.43)

Эти уравнения можно разрешить относительно параметров  и ⁺, тогда:

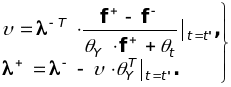(1.8.44)

Градиент от целевой функции по поисковым параметрам X из (1.8.36) определится как-

(1.8.45)

Таким образом градиент от целевой функции по параметрам X определяется по формуле (1.8.45) для расчета которой необходимо:

1) Решить слева направо систему (1.8.23) с граничными условиями (1.8.24).

2) Рассчитать граничные условия (1.8.42) и решить сопряженную систему уравнений (1.8.41) для множителей Лагранжа ^ справа налево. При этом в точках переключения t' эти переменные ^ будут иметь скачки в соответствии с формулой (1.8.44).

3) Одновременно с решением системы (1.8.41) можно рассчитывать интегралы, входящие в градиент (1.8.45). Окончательное значение градиента определяется по формуле (1.8.25) с учетом найденных по формулам (1.8.42) и (1.8.44) множителей  и .

Приведенный алгоритм позволяет ускорить расчет градиента приблизительно в (n 2)/(n+1) раз, т.к. причисленном расчете градиента c помощью приращений необходимо как минимум n+1 вычисление целевой функции, а в данном методе нужно только решить две системы дифференциальных уравнений (1.8.23) и (1.8.41), что приблизительно эквивалентно по времени вычислений двум расчетам целевой функции. Точность расчета градиента определяется шагом интегрирования систем дифференциальных уравнений. Следует отметить, что АУС-метод позволяет существенно ускорить процедуру расчета градиента в случае большого числа поисковых параметров - n. Однако составление и программирование сопряженной системы уравнений и расчет составляющих градиента требует существенных затрат на программирование и отладку программы. Поэтому этот метод следует использовать только для многократной оптимизации процессов в приборах с большим числом поисковых параметров ~ >10.