4. Линейное программирование. Задача оптимального распределения ресурсов при планировании выпуска продукции на предприятии

Линейное программирование — область математики, разрабатывающая теорию и численные методы решения задач нахождения экстремума (максимума или минимума) линейной функции многих переменных при наличии линейных ограничений, т. е. линейных равенств или неравенств, связывающих эти переменные.

f(x)=(c,x)→min(max), Ax≤{=,≥,<,>}b

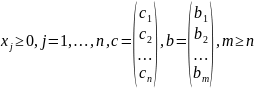(5)

Если из содержательного смысла экономической задачи следует, что x_ij≥0 должны быть целыми числами, то задача является задачей целочисленного линейного программирования. К задачам линейного программирования, например, относятся задачи оптимального распределения ресурсов при планировании выпуска продукции на предприятии (задача об ассортименте) и задача на максимум выпуска продукции при заданном ассортименте;

Задача оптимизации с нелинейным ограничениями X, заданными системой конечного числа уравнений:

f(x)→min, X={x∈Rⁿ, g_i(x)=0, i=1,…,m}. (6)

Здесь предполагается, что n<m, g∈R^m.

Для решения задачи (6) используется метод множителей Лагранжа. Основная идея метода заключается в переходе от задачи на условный экстремум исходной функции f(x) к задаче на безусловный экстремум.

Некоторая специально построенная функция Лагранжа L(x,λ):

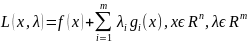. (7)

Необходимое условие локальной оптимальности. Пусть f(x), g_i(x) дифференцируемы в точке x*∈Rⁿ. Если x* — точка локального экстремума, то существует вектор λ*, компоненты которого не равны нулю одновременно, такой, что

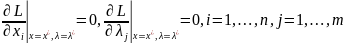. (8)

При этом должны выполняться условия регулярности: градиенты должны быть линейно независимы. Это означает, что ранг матрицы A_g, строками которой являются градиенты , должен быть равен m.

Любая точка x*, удовлетворяющая при некотором ненулевом векторе λ* условиям (8), называется стационарной точкой задачи (6). Для определения характера стационарных точек используется достаточное условие оптимальности с привлечением матрицы вторых частных производных функции Лагранжа по x_i.

Достаточное условие локальной оптимальности.

Пусть f(x), g_i(x) дважды дифференцируемы в точке x*, причём при некотором λ*≠0 выполняются условия (8), т. е. x* — стационарная точка. Тогда, если (A(x, λ)x, x)>0, ((A(x, λ)x, x)<0) при всех ненулевых x таких, что 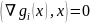, то x* — точка локального минимума (максимума) f(x) на множестве X.

Вектор x=(x₁,x₂,…,x_n)^T, компоненты которого удовлетворяют функциональным и прямым ограничениям задачи, называется планом (или допустимым решением) задачи линейного программирования. Допустимое решение, которое доставляет максимум или минимум целевой функции f(x), называется оптимальным планом задачи и обозначается x*. Прежде чем построить математическую модель задачи, т. е. записать её с помощью математических символов, необходимо четко разобраться с экономической ситуацией, описанной в условии. Для этого нужно ответить на вопросы:

1. Что является искомыми величинами задачи?

2. Какова цель решения?

3. Какой параметр задачи (прибыль, себестоимость, время и т. д.) служит критерием оптимальности решения?

4. В каком направлении (к максимуму или к минимуму) должно изменяться значение этого параметра для достижения наилучших результатов?

5. Какие условия в отношении искомых величин и ресурсов задачи должны быть выполнены?

Эти условия устанавливают, как должны соотноситься друг с другом различные параметры задачи (например, количество ресурса, затраченного при производстве, и его запас на складе; количество выпускаемой продукции и ёмкость склада, где она будет храниться; количество выпускаемой продукции и рыночный спрос на эту продукцию). После ответа на все эти вопросы можно приступать к записи математической модели.

Задача оптимального распределения ресурсов при планировании выпуска продукции на предприятии (задача планирования производства, задача об ассортименте).

Предположим, что предприятие выпускает n различных изделий. Для их производства требуются m различных видов ресурсов (сырья, вспомогательных материалов, рабочего и машинного времени). Эти ресурсы ограничены и составляют в планируемый период b условных единиц. Известны также технологические коэффициенты a_ij, которые указывают, сколько единиц i-го ресурса требуется для производства изделия j-го вида (i=1,…,m, j=1,…,n). Пусть прибыль, получаемая предприятием при реализации единицы изделия j-го вида, равна c_j. В планируемый период все показатели b_i, a_ij и c_j предполагаются постоянными. Требуется составить такой план выпуска продукции, при реализации которого прибыль предприятия была бы наибольшей. Другими словами, требуется составить оптимальный план работы предприятия x*, т. е. найти такие значения переменных x_i (объем выпуска продукции каждого вида), чтобы обеспечить предприятию получение максимальной прибыли от реализации всей продукции и чтобы на её производство хватило имеющихся в распоряжении ресурсов. Получим задачу (5).

Если задача (5) состоит из равенств и неравенств, то задача (5) называется общей, если из одних равенств и l=n, то канонической (симметричной), если из одних неравенств — стандартной. Указанные выше три формы задачи линейного программирования — общая, стандартная, каноническая — эквивалентны в том смысле, что каждая из форм с помощью несложных преобразований может быть переписана в форме другой задачи.

1. В том случае, когда требуется найти минимум функции f(x)=(c,x), можно перейти к нахождению максимума функции f₁(x)=−(c,x), поскольку min(f(x))=−max{−(c,x)}.

2. Ограничение-неравенство исходной задачи линейного программирования, имеющее вид «≤», можно преобразовать в ограничение-равенство добавлением к его левой части дополнительной неотрицательной переменной, а ограничение-неравенство вида «≥» — в ограничение-равенство вычитанием из его левой части дополнительной неотрицательной переменной:

a_i1x₁+…+a_inx_n≤b_i→a_i1x₁+…+a_inx_n+x_n+1=b_i, x_n+1>0 (6)

a_i1x₁+…+a_inx_n≥b_i→a_i1x₁+…+a_inx_n−x_n+1=b_i, x_n+1>0 (6)

Вводимые дополнительные переменные имеют вполне определённый экономический смысл. Так, если в ограничениях исходной задачи линейного программирования отражается расход и наличие производственных ресурсов, то числовое значение дополнительной переменной в плане задачи, записанной в форме основной, равно объёму неиспользуемого соответствующего ресурса. Задача (5) в каноническом виде:

f(x)=(c,x)→max, Ax=b

(5)

.

Основным (базисным) решением m уравнений с n неизвестными называется решение, в котором все n−m переменных равны нулю. Всего может быть k≤C_n^m основных переменных.

Допустимые базисные решения называют еще опорными планами.

Базисное решение, в котором хотя бы одна переменная равна нулю, называется вырожденным.

Теорема. Если ранг линейной системы равен m, то произвольному набору неосновных переменных соответствует одно решение системы (7).