|
42.
Уравнения Максвелла
Дифференциальная
форма:
1-я
пара уравнений Максвелла:
 , ,
 . .
Первое
из этих уравнений связывает значение
вектора E
с изменениями вектора B
во времени и явл-ся выражением закона
электромагнитной индукции.
2-е
ур-ие указ. на отсутствие источников
магнитного поля, т.е. магнитных зарядов.
2-я пара ур-ий Максвелла:
 , ,
 .
Первое уравнение устанавливает связь
между токами проводимости и смещения
и порождаемым ими магнитным полем.
Второе показывает, что источниками
вектора D
служат сторонние заряды. Каждое из
векторных уравнений (первые уравнения
в каждой паре) эквивалентно трем
скалярным уравнениям: .
Первое уравнение устанавливает связь
между токами проводимости и смещения
и порождаемым ими магнитным полем.
Второе показывает, что источниками
вектора D
служат сторонние заряды. Каждое из
векторных уравнений (первые уравнения
в каждой паре) эквивалентно трем
скалярным уравнениям:
 , ,
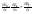 , ,

 , ,
 , ,
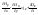 .
Чтобы произвести расчет полей, нужно
дополнить уравнения Максвелла
уравнениями, связывающими вектора D
и j
с E,
а также H
с B: .
Чтобы произвести расчет полей, нужно
дополнить уравнения Максвелла
уравнениями, связывающими вектора D
и j
с E,
а также H
с B:
 , ,
 , ,
 .
Сов-ть этих ур-ий образует основу
электродинамики покоящихся сред. .
Сов-ть этих ур-ий образует основу
электродинамики покоящихся сред.
Интегральная
форма: Первая пара уравнений Максвелла: , ,
 .
Вторая пара уравнений Максвелла: .
Вторая пара уравнений Максвелла: , ,
 . .
|


 ,
,
 .
. ,
,
 .
Первое уравнение устанавливает связь
между токами проводимости и смещения
и порождаемым ими магнитным полем.
Второе показывает, что источниками
вектора D
служат сторонние заряды. Каждое из
векторных уравнений (первые уравнения
в каждой паре) эквивалентно трем
скалярным уравнениям:
.
Первое уравнение устанавливает связь
между токами проводимости и смещения
и порождаемым ими магнитным полем.
Второе показывает, что источниками
вектора D
служат сторонние заряды. Каждое из
векторных уравнений (первые уравнения
в каждой паре) эквивалентно трем
скалярным уравнениям: ,
,
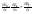 ,
,

 ,
,
 ,
,
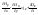 .
Чтобы произвести расчет полей, нужно
дополнить уравнения Максвелла
уравнениями, связывающими вектора D
и j
с E,
а также H
с B:
.
Чтобы произвести расчет полей, нужно
дополнить уравнения Максвелла
уравнениями, связывающими вектора D
и j
с E,
а также H
с B: ,
,
 ,
,
 .
Сов-ть этих ур-ий образует основу
электродинамики покоящихся сред.
.
Сов-ть этих ур-ий образует основу
электродинамики покоящихся сред. ,
,
 .
Вторая пара уравнений Максвелла:
.
Вторая пара уравнений Максвелла: ,
,
 .
.