Семестр 03 / Шпоры на экзамен / 41

41. Ток смещения. Полный ток. В случае стационарного электромагн. поля ротор = в каждой т. плотности тока провод-ти: (*). Связав с плотностью заряда в той же т. ур-ем непрерывности: . Электромагн. поле мб стационарным лишь при условии, что плотность ρ и плотность тока не зависят от времени. В этом случае дивергенция =0. Поэтому линии тока не имеют источников и явл-ся замкнутыми. Рассмотрим магн. поле, создаваемое током, текущим при зарядке конденсатора от источника пост. напряж. U. Возьмем круговой контур Г, охватывающий провод, по котор. течет ток к конденсатору, и проинтегрируем отношение (*) по пересекающей провод пов-ти ограниченной контуром: . Преобразовав левую часть по теор Стокса, получ циркул. по контуру Г: . Проделав такие же вычисления для пов-ти , не пересекающей провод с током, придем к явно неверному соотнош. . Получ. рез-тат указ. на то, что в случае изменяющихся со временем полей уравнение (*) перестает быть справедливым. Для согласования ур-ий Максвелл ввел в правую часть уравнения (*) доп. слагаемое. Максвелл назвал его плотность тока смещения. Т.о., ур-ие (*) должно иметь вид: . Сумму тока проводимости и тока смещения принято наз. полным током. Плотность полного тока . Если положить дивергенцию тока смещения = дивергенции тока проводимости, взятой с обратным знаком: , то . . Дивергенция вектора электрич. смещения = плотности сторонних q: . Продифференцировав по t получим: . Поменяем в левой части порядок дифференц-ия по t и по координатам. В рез-те придем к выраж. для производной по : . , отсюда . , кот. как и ур-ие (, где (потенциальное + вихревое)) явл-ся одним из основных в теории Максвелла. Ток смещения – условный термин. Из физических св-в - способен создать магн. поле. Убедимся в том, что поверхностный интеграл имеет одинаковое значение для и . Через пов-ть «течет» как ток проводимости, так и ток смещения, обусловленный электрич. полем, имеющимся вне конденсатора. След-но, для 1-й пов-ти: . Для второй пов-ти 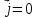, след-но, . Разность интегралов . Заменив на , а на , получ: . Для тока смещения, как и для тока проводимости, можно строить линии тока. Электр. смещ. в зазоре конденсатора = поверхностной плотности q на обкладке: 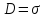. Отсюда . Левая часть дает плотность тока смещения в зазоре, правая часть – плотность тока проводимости внутри обкладок. Рав-во этих плотностей означ, что на границе обкладок линии тока провод-ти непрерывно переходят в линии тока смещения. След-но, линии полного тока оказываются замкнутыми.