
- •Родионов в.И.
- •Конспект лекций
- •«Электрический привод»
- •Содержание
- •Лекция 1
- •Функциональная схема автоматизированного электропривода
- •Типы электроприводов
- •Лекция 2 Механическая часть силового канала электропривода
- •Кинематическая схема электрического привода
- •Нагрузки к валу электродвигателя
- •Приведение моментов инерции нагрузки к валу двигателя
- •Лекция 3 Механические характеристики производственных механизмов и электрических двигателей
- •Механические характеристики механизмов
- •Механические характеристики электродвигателей
- •Лекция 4 Уравнения движения электропривода
- •Время ускорения и замедления привода
- •Определение оптимального передаточного отношения редуктора
- •Лекция 5 Механические характеристики электропривода постоянного тока с двигателем независимого возбуждения
- •Механические характеристики двигателя последовательного возбуждения
- •Механические характеристики двигателя смешанного возбуждения
- •Лекция 6 Тормозные режимы двигателей постоянного тока независимого возбуждения
- •Тормозные режимы двигателя последовательного возбуждения
- •Тормозные режимы двигателя смешанного возбуждения
- •Лекция 7 Механические характеристики асинхронного электропривода
- •Механическая и угловая характеристики синхронного электропривода
- •Лекция 8 переходные режимы в электроприводах
- •Пуск двигателя постоянного тока независимого возбуждения до основной угловой скорости
- •Ударное приложение нагрузки
- •Лекция 9 способы регулирования угловой скорости. Регулирование угловой скорости электропривода постоянного тока с двигателем независимого возбуждения
- •1. Рассказать о регулировании угловой скорости изменением
- •Регулирование угловой скорости изменением магнитного потока
- •Лекция 10 реостатное и импульсное параметрическое регулирование
- •Лекция 11 регулирование изменением напряжения на якоре
- •1. Регулирование изменением напряжения на якоре.
- •2. Система «генератор-двигатель».
- •Система «генератор-двигатель»
- •16.1. Механические характеристики двигателя постоянного тока независимого возбуждения при различных напряжениях.
- •16.2. Принципиальная схема включения двигателя постоянного тока независимого возбуждения по системе г-д.
- •Управляемые выпрямители
- •Лекция 12 Широтно-импульсные преобразователи и шУнтирование якоря
- •Регулирование угловой скорости двигателя постоянного тока независимого возбуждения шунтированиЕм якоря
- •18.3. Механическая характеристика двигателя постоянного тока независимого возбуждения при шунтировании обмотки якоря
- •18.4. Семейство механических характеристик при неизменном сопротивлении шунтирующего резистора и различных сопротивлениях последовательного резистора
- •Лекция 13 Регулирование угловой скорости двигателя постоянного тока последовательного возбуждения
- •Регулирование угловой скорости двигателя постоянного тока последовательного возбуждения шунтированием обмотки якоря или обмотки возбуждения
- •Лекция 14 Выбор электродвигателЯ
- •Нагревание и охлаждение электродвигателя
- •Выбор мощности электродвигателя для продолжительного режима
- •Лекция 15 Выбор электродвигателЯ для кратковременного и повторно-кратковременного режима
- •Выбор мощности электродвигателя для кратковременного режима
- •Выбор мощности электродвигателя для повторно-кратковременного режима
- •Дополнительная литература
Лекция 5 Механические характеристики электропривода постоянного тока с двигателем независимого возбуждения
План лекции:
Электромеханические характеристики двигателя постоянного тока независимого возбуждения.
2. Механические характеристики электропривода постоянного тока независимого возбуждения.
Схема включения двигателя постоянного тока независимого возбуждения представлена на рис 6.1. Якорь двигателя и его обмотка возбуждения ОВ получают питание источников напряжения U и UВ
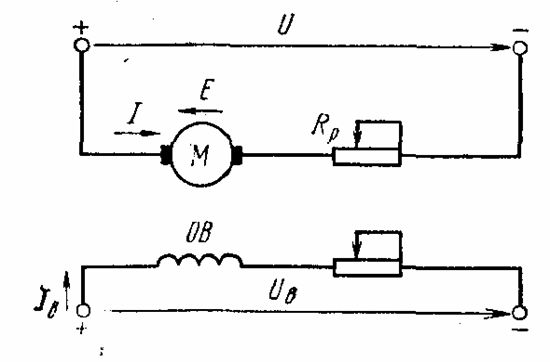
Рис.6.1. Схема включения двигателя постоянного тока
независимого возбуждения
Направления тока I и ЭДС вращения двигателя Е, показанные на рис. 6.1, соответствуют двигательному режиму работы, когда электрическая энергия потребляется двигателем из сети и преобразуется в механическую энергию, мощность которой равна Р = М . Зависимость между М и двигателя определяется его механической характеристикой.
Выражение для механической характеристики двигателя может быть получено из уравнения равновесия напряжений, составленного для якорной цепи схемы:
![]() (6.1)
(6.1)
где I - ток в якорной цепи двигателя, А; R - суммарное сопротивление якорной цепи, Ом, включающее внешнее сопротивление резистора Rp и внутреннее сопротивление якоря двигателя Rя (при наличии дополнительных полюсов учитывается и их сопротивление);
![]() (6.2)
(6.2)
где k — коэффициент, зависящий от конструктивных данных двигателя, k=pN/2πа (р — число пар полюсов двигателя; N — число активных проводников обмотки якоря; а — число пар параллельных ветвей обмотки якоря); Ф и — соответственно магнитный поток, Вб, и угловая скорость двигателя, рад/с.
Подставим в (6.1) значение Е из (6.2), и получим выражение для скорости двигателя
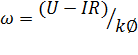 (6.3)
(6.3)
Такую зависимость =f(I) называют электромеханической характеристикой двигателя.
Для получения механической характеристики необходимо учесть, что момент, развиваемый двигателем, связан с током якоря и магнитным потоком зависимостью:
![]() (6.4)
(6.4)
Подставив в (3.3) значение тока I, найденное из (6.4), получим выражение для механической характеристики двигателя:
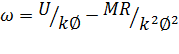 (6.5)
(6.5)
или 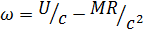 (6.6)
(6.6)
где
![]() (6.7)
(6.7)
Коэффициент с принимается постоянным, не зависящим от нагрузки, если у двигателя с независимым возбуждением имеется компенсационная обмотка. Он может считаться неизменным, если для обычных двигателей пренебречь реакцией якоря.
Механическая характеристика двигателя при неизменных параметрах U, Ф и R является прямой линией. На рис. 6.2 представлены механические характеристики двигателя независимого возбуждения для различных сопротивлений якорной цепи.
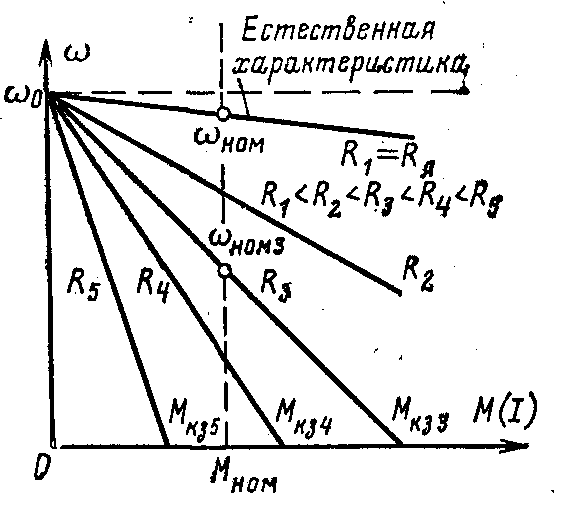
Рис. 6.2. Естественная и реостатные механические характеристики двигателя постоянного тока независимого возбуждения
Как видно из (6.5), при М
= 0 все характеристики
проходят через одну точку, лежащую на
оси ординат. Угловая скорость в этой
точке имеет вполне определенное значение,
не зависящее от сопротивления якорной
цепи. Эта скорость носит название
скорости идеального холостого хода
![]() и
определяется выражением
и
определяется выражением
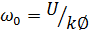 (3.8)
(3.8)
При скорости идеального холостого хода, когда ток в якорной цепи равен нулю, ЭДС якоря, направленная навстречу приложенному напряжению, равна ему по абсолютному значению. Если двигатель до приложения нагрузки работал с угловой скоростью , то при появлении на его валу момента сопротивления угловая скорости будет снижаться. Следствием этого будет уменьшение ЭДС вращения Е согласно (6.2) и увеличение тока якоря в соответствии с (6.1) и момента двигателя по (6.4).
Угловая скорость будет снижаться до тех пор, пока момент двигателя не сравняется с моментом сопротивления. Разность значений установившихся скоростей электропривода до и после приложения заданной статической нагрузки называется статическим падением скорости электропривода.
Второй член (3.6) характеризует собой статическое падение угловой скорости относительно угловой скорости идеального холостого хода:
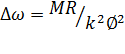 (6.9)
(6.9)
Таким образом, уравнение для скорости двигателя может быть записано так:
![]() (6.10)
(6.10)
Верхняя характеристика на рис. 3.2, носит название естественной. Она получается при отсутствии внешних резисторов в якорной цепи и номинальных значениях напряжения и магнитного потока двигателя. Жесткость естественной характеристики зависит от внутреннего сопротивления якорной цепи двигателя Rя. Внутреннее сопротивление якорной цепи включает собственное сопротивление якорной обмотки, сопротивление обмотки дополнительных полюсов, компенсационной обмотки и щеток. Соответственно перепад скорости для естественной характеристики
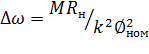 (6.11)
(6.11)
При дополнительно включенном реостате, имеющем сопротивление Rр, статическое падение скорости определится из соотношения
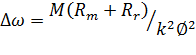 (6.12)
(6.12)
Разделив (6.10) на , получим статическое падение скорости в относительных единицах:
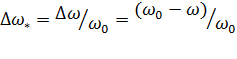 (6.13)
(6.13)
Статическое падение скорости
в относительных единицах
![]() аналогично скольжению асинхронного
двигателя, хотя имеет другой смысл.
аналогично скольжению асинхронного
двигателя, хотя имеет другой смысл.
Построение естественной механической характеристики удобно производят по двум точкам, одна из которых соответствует номинальному электромагнитному моменту двигателя и номинальной скорости (М = Мном и = ном), а другая — скорости идеального холостого хода (М = 0 и = ). Номинальная скорость двигателя определяется по паспортным данным.
Номинальный электромагнитный момент вычисляется по формуле
![]() (6.14)
(6.14)
Скорость идеального холостого хода может быть получена из (6.8), если числитель и знаменатель ее умножить на и учесть, что
![]() (6.15)
(6.15)
Тогда
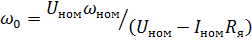 (6.16)
(6.16)
Так как в каталогах внутреннее
сопротивление якоря Rя
обычно не указывается,
то его ориентировочно определяют,
принимая, что половина всех потерь в
двигателе при номинальной нагрузке
связана с потерями в меди якоря. Поэтому
![]() .
Отсюда
.
Отсюда
 (6.17)
(6.17)
Пользуясь естественной механической характеристикой, легко построить и реостатную характеристику при любом сопротивлении реостата Rp. Угловая скорость ном,р определяется по формуле
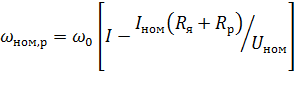 . (6.18)
. (6.18)
Механическая характеристика может быть построена также по точке идеального холостого хода и точке, соответствующей режиму короткого замыкания, где М = MK3, а скорость = 0. Угловую скорость определяем по (6.15,6.16), а момент Мкз, пренебрегая реакцией якоря, - по формуле
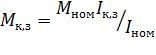 , (6.19)
, (6.19)
где Iкз = U/R —ток короткого замыкания; R = RЯ + Rp.
С учетом сказанного уравнение механической характеристики представляется в следующем виде:
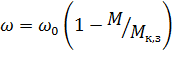 . (6.20)
. (6.20)
