Время ускорения и замедления привода

Время переходных режимов привода: пуска, торможения, перехода от одной скорости к другой влияет на производительность механизма. Определение времени переходных процессов основано на интегрировании уравнения движения привода (5.2). Разделяя переменные, полу­чаем:

_(5.4)

Время, необходимое для изменения скорости привода от до ,

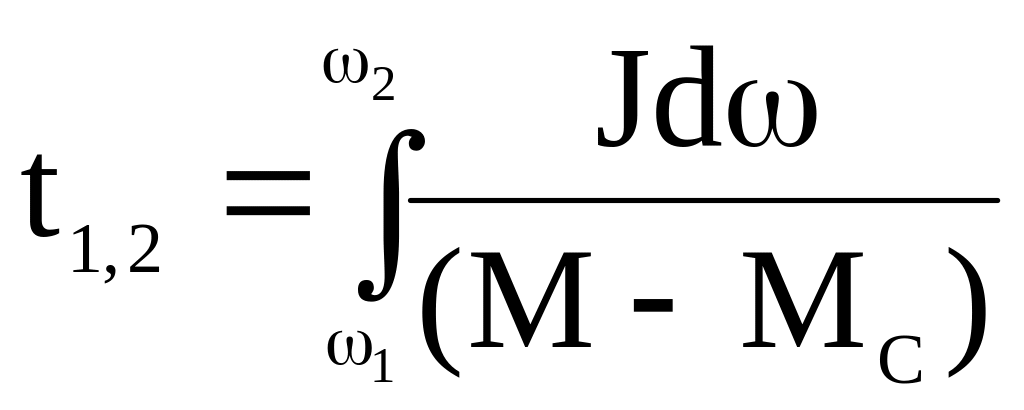. (5.5)

Для решения этого интеграла необходимо знать зави­симости моментов двигателя и сопротивления от скорости.

В простейшем случае, приняв М =const, Мс = const, = const, получим

. (5.6)

Этим уравнением можно воспользоваться, например, для расчета времени пуска привода. Если значение момента двигателя во время пуска обозначить через М_п, как это показано на рис. 5.1, то получим следующее выражение для времени пуска от состояния покоя до конечной скорости , соответствующей заданному моменту сопро­тивления:

. (5.7)

Если требуется точно учесть время переходного про­цесса и момент двигателя не может быть принят постоян­ным, например, при пуске двигателя с короткозамкнутым ротором, необходимо пользоваться (5.1). При этом следует иметь в виду, что момент инерции для большинства приводов имеет постоянное значение, а момент двигателя и момент сопротивления в переходных режимах обычно не остаются постоянными.

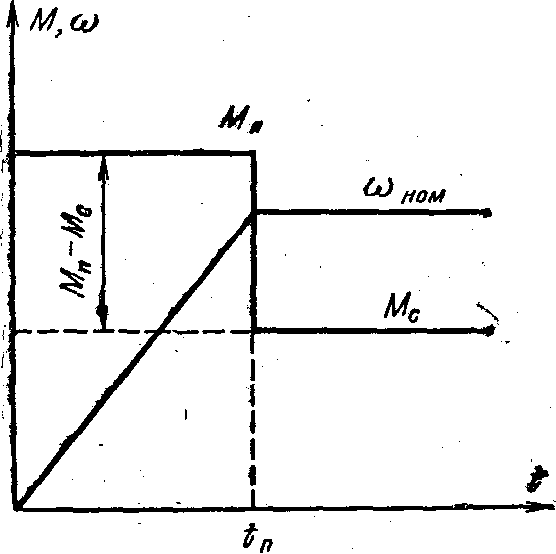
Рис. 5.1. Пусковой график электропривода

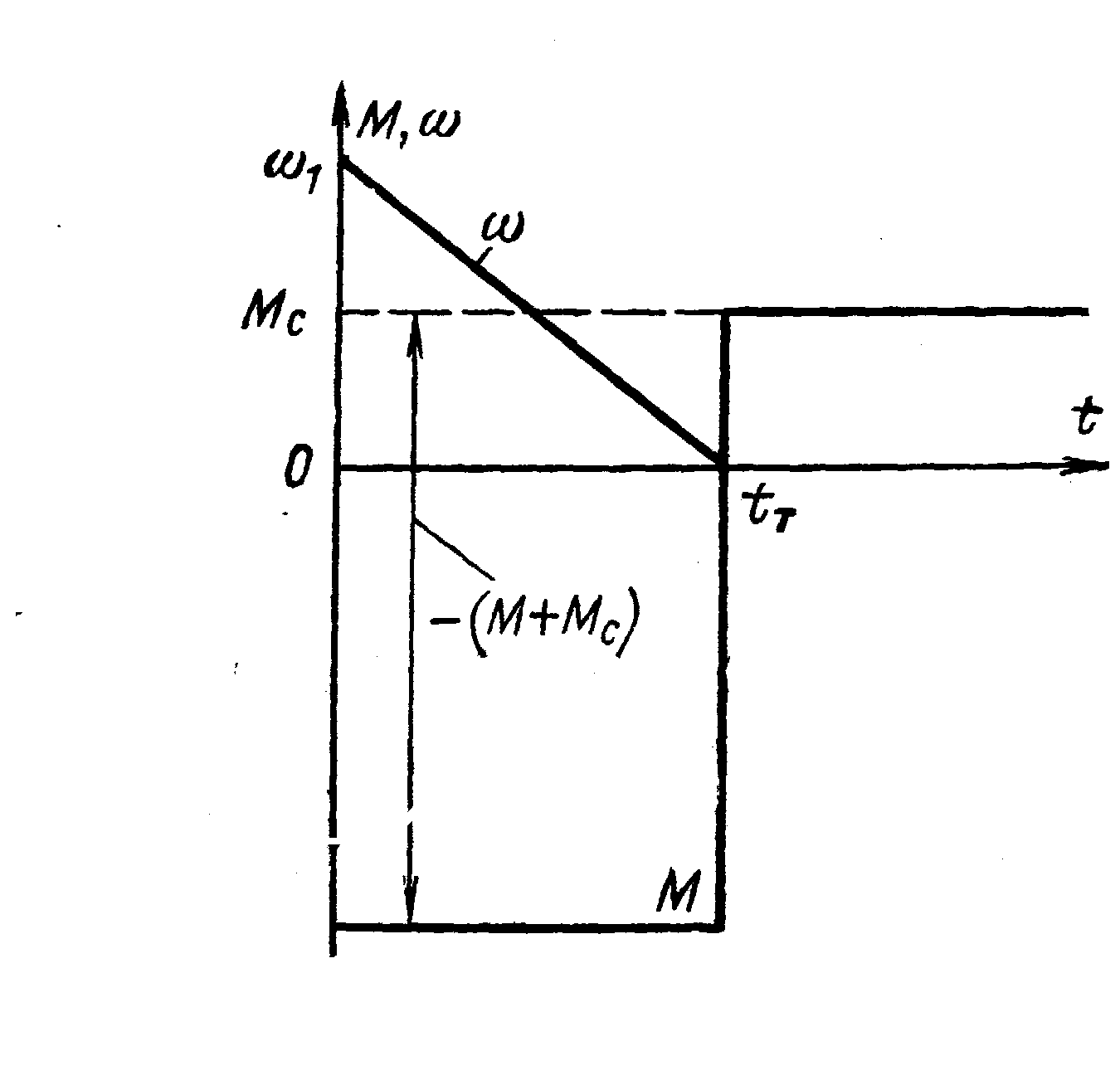
Рис. 5.2. График торможения электропривода

Из формулы (5.1) видно, что теоретически полное время пере­ходного процесса равно бесконечности. Действительно, поскольку переходный процесс заканчивается при наступлении равенства моментов (М = Мс), то величина, стоящая под знаком интеграла, стремится к бесконечности. В прак­тических расчетах обычно считают, что процесс разбега заканчивается при скорости, равной приблизительно = 0,95 , тогда время разбега получит конечное значение.

В тех случаях, когда динамический момент имеет отрицательное значение, привод замедляется. Как указывалось выше, для такого случая уравнение моментов будет иметь вид:

. (5.7)

Очевидно, привод замедляется и в том случае, когда двигатель развивает положительный момент по абсолютному значению, меньший момента сопротивления.

Определение оптимального передаточного отношения редуктора

Из последнего уравнения следует, что время торможения

= . (5.8)

Полагая в частном случае J = const, М = const и М_с = const, получаем:

. (5.9)

Пользуясь уравнением (5.9), можно рассчитать время торможения

( = 0) для графика момента, показанного на рис. 5.2.

Если момент двигателя и момент статический находятся в сложной зависимости от скорости, уравнение движения аналитически не решается. В этом случае приходится пользоваться приближенными графическими или графо­аналитическими методами решения.

В ряде практических случаев (например, в следящих системах, приводах вспомогательных механизмов прокатных станов, продольно-строгальных станках и т. п.) возникает необходимость в получении минимального времени разгона и торможения производственного механизма с целью повышения его производительности. При заданных значениях моментов инерции ротора двигателя, произ­водственного механизма и момента сопротивления уравнение движения привода относительно рабочего вала механизма (пренебрегая потерями в передачах) может быть записано так:

, (5.10)

где — коэффициент, учитывающий момент инерции пере­дач.

Очевидно, минимум времени разгона имеет место при наибольшем ускорении. Из (5.10) получим

. (5.11)

Пользуясь правилом определения максимума ( ) и полагая М_с = const, а также М = const (средним за период переходного режима), находим оптимальное передаточное отношение i. Для этого продифференцируем по времени правую часть выражения (5.11) и числитель полученной дроби приравняем нулю:

;

или

.

Решением этого уравнения является следующее выражение:

. (5.12)

В том случае, когда момент сопротивления оказывается значительно меньшим момента двигателя при пуске и торможении,

. (5.13)