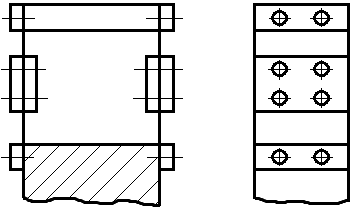
31. Упругие направляющие

Движение каретки осуществляется за счет деформации упругих элементов.

Основные разновидности:

1. П лоско-пружинный параллелограмм

1 – каретка

2 – плоские пружины

3 – крепёжные накладки

4 – накладки для жесткости

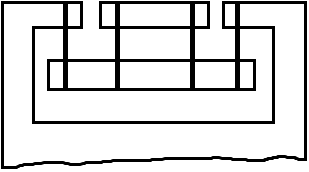
5

4

1 – основная каретка

2 – вспомогательная каретка

3 – основание

4, 5 – плоские пружины

3. Мембранные направляющие

1 – каретка

2 – мембрана

32. Зубчатые передачи. Классификация. Классификация зубчатых передач:

1. По взаимному расположению осей:

• С параллельными осями

• С пересекающимися осями

• Со скрещивающимися осями (червячные, гипоидные, винтовыми колесами)

2. По направлению зубьев:

• Прямоугольные

• Косозубые

• Шевронные

• С криволинейными зубьями

3. По характеру движения осей:

• С неподвижными осями (рядовые)

• С подвижными осями (планетарные)

4. По профилю зубьев:

• Эвольвентные

• Циклоидальные

• Передачи с защемлением Новикова

5. По назначению:

• Кинематические (для обеспечения заданного U с требуемой точностью)

• Силовые (для передачи крутящего момента)

33. Силовой расчет зубчатых передач

Расчет выполняется в 2 этапа:

1. проектный

2. проверочный

Для закрытых передач, работающих со смазкой, проектным является расчет на контактную прочность зубьев, при этом расчетные параметры это межосевое расстояние и делительный диаметр. Для конических передач – конусное расстояние.

При проверочном расчете уточняют модуль передачи, исходя из прочности на изгиб.

Для открытых передач, работающих без смазки, расчет выполняют наоборот:

Последовательность расчета:

Из условия контактной прочности расчитывают межосевое расстояние:

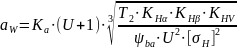
– коэффициент межосевого расстяния, зависит от вида передачи

– передаточное отношение

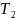– вращающий момент на зубчатом колесе

– коэффициент распредеоенной нагрузки по длине зуба

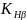– коэф. концентрации нагрузки (в зависимости от расположения зубчатого колеса на валу)

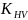– коэффициент окружной скорости (зависит от скорости вращения и материала колеса)

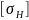– допускаемое контактное напряжение

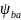– отношение ширины колеса к межосевому расстоянию (

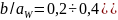
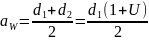
Полученное значение модуля 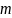округляют до ближайшего большего стандартного, потом расчитывают диаметры колес и межосевое расстояние.

Далее выполняют проверочный расчет на изгиб зубьев. Расчетным параметром является модуль:

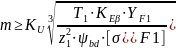
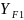– коэффициент формы зуба

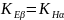
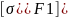– допустимое напряжение в материале

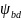– относительная ширина колеса

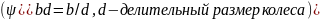
Если полученный модуль больше ранее выбранного, его округляют в большую сторону и назначают для передачи.

Для открытых передач расчет выполняют в обратном порядке.

34. Червячные передачи.

Являются предельным случаем гиперболоидных зубчатых передач.

Передаточное отношение рекомендуется выбирать в пределах

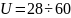
При этом червяк имеет число заходов 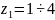, а у червячного колеса минимальное число зубьев

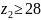
Используют несколько разновидностей червяков. Наиболее распространены Архимедовы (ZA), конвалютные (ZN1) и эвольвентные (Z1).

1. Архимедов червяк имеет витки с прямолинейным профилем в осевом сечении.

А - А

Форма зубьев удобна для нарезания на токарном станке и не удобна для шлифования. Данные червяки используют при невысоких требованиях к точности и небольших нагрузках. Изготавливают их из незакаленной стали.

2. Конвалютный червяк имеет прямоугольные профиль витков в нормальном сечении, поэтому такие червяки легко шлифуются.

3. Эвольвентные червяк имеет эвольвентные профиль зуба в торцовом сечении. Поэтому для его изготовления можно использовать стандартное зуборезное оборудование.

Расчет аналогичен расчету зубчатых передач.

Достоинства:

• Высокое передаточное отношение

• Передача движения между скрещивающимися осями

Недостатки: низкий КПД