Косая плоскость

Косой плоскостью называется поверхность, образованная движением прямой линии, скользящей по двум скрещивающимся прямым и остающейся во всех своих положениях параллельной некоторой плоскости параллелизма. Косая плоскость, направляющими которой являются скрещивающиеся прямые m(m₁,m₂) и n(n₁,n₂), а плоскостью параллелизма - плоскость П₁, показанная на рис. 2.3.35. Р ис. 2.3.35

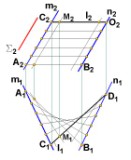
Ту же самую поверхность можно получить, если за направляющие прямые принять любую пару образующих, например АВ(А₁В₁, А₂В₂) и СD(С₁D₁, С₂D₂), за образующую прямую - одну из направляющих (m или n) и за плоскость параллелизма - плоскость ( ₂), параллельную прямым m и n. Таким образом, косая плоскость имеет два семейства прямолинейных образующих и две плоскости параллелизма. Образующие одного семейства - скрещивающиеся прямые, каждая образующая одного семейства пересекает все образующие второго. Поэтому через каждую точку поверхности проходят две прямолинейные образующие разных семейств. Косую плоскость называют также гиперболическим параболоидом, так как при пересечении ее соответствующими плоскостями в сечении можно получить параболы и гиперболы. Геометрическая часть определителя косой плоскости состоит из направляющих прямых и плоскости параллелизма: Алгоритмическая часть определителя состоит из указания о том, что любая образующая поверхности может быть построена как прямая, пересекающая направляющие прямые и параллельная плоскости параллелизма.

Р ис. 2.3.36 (анимация)

Анимация (рис. 2.3.36) поясняет формирование косой плоскости, как поверхности с плоскостью параллелизма. Образующие косой плоскости формируются вспомогательной плоскостью, перемещающейся параллельно плоскости параллелизма. Аанимационный слайд 2.3.37 демонстрирует одно из свойств косой плоскости - наличие второй плоскости параллелизма. Видно, что для косой плоскости, построенной в предыдущем примере, существует второе семейство образующих, которые могут быть получены перемещением другой вспомогательной плоскости со своей, второй плоскостью параллелизма. Р ис. 2.3.37

На рис. 2.3.38 поясняется существование семейства параболических сечений. Косая плоскость может быть получена как поверхность Каталана путем плоскопараллельного перемещения одной из парабол, как образующей, по второй параболе, как направляющей. Результат этого кинематического варианта формирования косой плоскости показан на рис. 2.3.39, где представлена та же косая плоскость, что и в предыдущих примерах, но с другим каркасом.

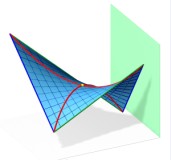Рис. 2.3.38 Рис. 2.3.39

На рисунке так же показан пример гиперболического сечения рассматриваемой поверхности и его вырожденный случай - две прямые, проходящие через "седловую" точку.

Винтовые поверхности

Поверхность, образованная винтовым движением прямой линии, называется линейчатой винтовой поверхностью - геликоидом (винтовое движение характеризуется вращением вокруг некоторой оси i и поступательным перемещением, параллельным этой оси).

а. Прямой геликоид

Р ис. 2.3.40

Если в качестве кривой направляющей коноида взять цилиндрическую винтовую линию, в качестве прямой направляющей - ось винтовой линии, а за плоскость параллелизма - плоскость, перпендикулярную оси винтовой линии, то поверхность, образованная при этих условиях, называется винтовым коноидом или прямым геликоидом (рис. 2.3.40). Очевидно, что образующая прямая прямого геликоида пересекает ось под прямым углом. На рис. 2.3.41 показана кинематика построения прямого открытого геликоида. Видно, как образующая прямая перемещается параллельно плоскости основания (плоскость параллелизма) и в каждый момент пересекает две направляющие: винтовую линию и прямую - ось этой винтовой линии. 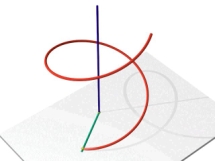Рис. 2.3.41 анимация Рис. 2.3.42

На рис. 2.3.42 приведен пример прямого открытого геликоида, имеющего конечную толщину поверхности.

б. Наклонный геликоид

Наклонным геликоидом называется поверхность, образованная движением прямой линии, cкользящей по двум направляющим (одна из них цилиндрическая винтовая линия, а вторая - ось винтовой линии) и сохраняющей во всех положениях постоянный угол с направляющей плоскостью, которую располагают перпендикулярно оси винтовой поверхности. При построении проекций наклонного геликоида удобно пользоваться направляющим конусом. Р ис. 2.3.43

Направляющий конус соосен с винтовой поверхностью, его образующие наклонены под углом к плоскости основания. Образующая прямая перемещается по направляющим и остается во всех своих положениях параллельной соответствующей образующей направляющего конуса. Таким образом, образующая прямая во всех своих положениях пересекает ось i под постоянным углом 90^o. Проекции наклонного геликоида построены на рис. 2.3.43 Геометрическая часть определителя наклонного геликоида состоит из направляющих линий (m и i) и угла . Алгоритмическая часть определителя состоит из указания о том, что любая образующая поверхности может быть построена как прямая, пересекающая направляющие линии и параллельная соответствуюшей образующей направляющего конуса. Плоскость, перпендикулярная оси поверхности, пересекает ее по спирали Архимеда (плоскость на рис. 2.3.43). Р ис. 2.3.44

Рассмотренные винтовые поверхности, так же как и поверхности вращения, обладают свойством сдвигаемости, т. е. поверхность может перемешаться вдоль самой себя без каких-либо деформаций. Это свойство поверхности широко используется в технике при создан1. Циклические поверхности

Циклической поверхностью называется поверхность, образованная непрерывным каркасом круговых сечений.

На циклической поверхности расположено, по крайней мере, одно семейство круговых образующих (постоянного или переменного радиуса). Задание циклической поверхности должно однозначно определять положение плоскости каждой окружности, положение в плоскости и величину радиуса.

Циклическую поверхность можно задать плоскостью параллелизма, направляющей а и линией, которой принадлежат центры семейства окружностей  (а, i, Г).

На рисунке показана поверхность  (а, i, Г), где плоскости окружности циклической поверхности параллельны плоскости проекций П1.