Способы образования и задания поверхностей

Кинематический способ.

Поверхность рассматривается как совокупность всех последовательных положений некоторой линии – образующей, перемещающейся в пространстве по определенному закону. Линия, которую пересекают все образующие поверхности, называется направляющей.

Упорядоченное множество линий, принадлежащих поверхности, называется ее каркасом. Обычно в качестве линий каркаса используют семейство образующих или семейство направляющих.

Каркасный способ.

Поверхность рассматривается как совокупность некоторого числа линий, образующих каркас. Основное отличие каркасных поверхностей от кинематических состоит в том, что для первых задается определенное число линий каркаса – дискретный каркас, а у вторых в любой точке поверхности может быть построена линия каркаса, т.е. поверхность имеет непрерывный каркас. Каркасные поверхности задают на чертеже проекциями линий каркаса. Точки и линии каркасной поверхности, не лежащие на линиях каркаса, могут быть построены только приближенно. Поэтому поверхность, заданная каркасом, не вполне определена. Могут существовать и другие поверхности с тем же каркасом, но несколько отличающиеся одна от другой в промежутках между каркасными линиями.

На эпюре Монжа поверхность задается проекциями ее репера.

Построение недостающей проекции точки, принадлежащей поверхности, осуществляется с помощью простейших линий каркаса поверхности, проходящих через эту точку. Для построения таких линий каркаса используют закон образования данной поверхности.

Следует отметить, что, умея строить одну точку поверхности, можно построить проекции любой линии, принадлежащей заданной поверхности, рассматривая эту линию, как совокупность отдельных точек.

Определитель и каркас

Поверхностью называется непрерывное двупараметрическое множество точек.

Для получения наглядного изображения поверхности на чертеже закон перемещения линии целесообразно задавать графически в виде совокупности линий и указаний о характере перемещения линии. Эти указания могут быть заданы графически, в частности с помощью направляющей поверхности. В процессе образования поверхностей линия может оставаться неизменной или менять свою форму. Такой способ образования поверхности называется кинематическим, а сама поверхность - кинематической.

На чертеже кинематическая кривая поверхность задается при помощи ее определителя. Определителем поверхности называют совокупность условий, необходимых и достаточных для задания поверхности в пространстве.

Подвижная линия называется образующей, неподвижные линии и поверхность - направляющими.

Каркасом поверхности принято называть упорядоченное множество точек или линий, принадлежащих поверхности.

В зависимости от того, чем задается каркас поверхности, точками или линиями, каркасы называют точечными или линейными. Линейным каркасом называется множество таких линий, которые имеют единый закон образования и связаны между собой определенной зависимостью. Условия связи между линиями каркаса называются зависимостью каркаса. Эта зависимость характеризуется некоторой изменяющейся величиной, которая называется параметром каркаса. Если параметр линейного каркаса является непрерывной функцией, то каркас называется непрерывным, а если параметр - прерывная функция, то каркас называется дискретным.

На рис. 7.2 приведен пример каркаса поверхности, состоящей из двух ортогонально расположенных семейств линий а₁, а₂, а₃,..., а_n, b₁, b₂, b₃,...b_n.

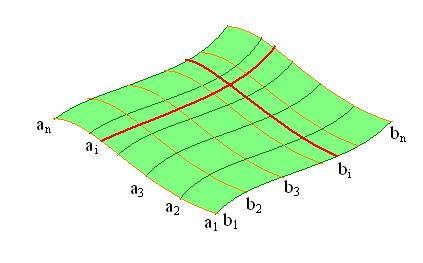
Рис. 7.2. Пример линейного каркаса поверхности