Знайти область збіжності ряду
.
Знайдемо радіус збіжності функціонального ряду:
.
Область збіжності: .
Перевіримо поведінку ряду на межах області.
При
отримаємо знакозмінний числовий ряд
,
розглянемо для нього ряд з модулів:
порівняємо його за граничною ознакою
збіжності рядів зі збіжним рядом Діріхлє
,
де
:
,
отже ряди
та
одночасно збіжні, а з цього випливає,
що ряд
є абсолютно збіжним.
При отримаємо числовий ряд з додатними членами , який є збіжним з попередніх міркувань.
Відповідь:
,
- область збіжності функціонального
ряду
.
За допомогою лишків обчислити контурний інтеграл:
,
якщо с:
.
.
Будуємо область інтегрування:
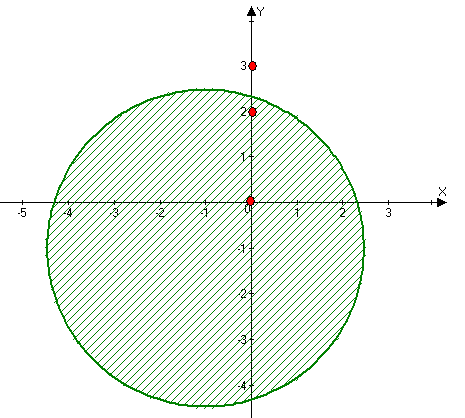
Даний інтеграл містить три
особливі точки:
,
,
.
Причому точка є усувною особливою точкою, а лишок в усувній особливій точці завжди дорівнює 0.
Особлива точка не належить області інтегрування.
Лишок в особливій точці , яка є простим полюсом, має вигляд:
Відповідь:
.
Розв’язати задачу Коші операційним методом
y′′ - 9y′ = f(t); y(0) = y′(0) = 0;
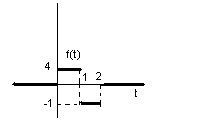
при умові
.
Отже
Операторне рівняння має наступний вигляд:
За теоремою запізнення:
