2. За допомогою лишків обчислити контурний інтеграл:

, якщо с: .

.

Будуємо область інтегрування:

Маємо одну особливу точки , яка є полюсом 4-го порядку, тоді лишок по точці :

Відповідь: .

3. Розв’язати задачу Коші операційним методом

y′′ + 4y = f(t); y(0) = y′(0) = 0;

.

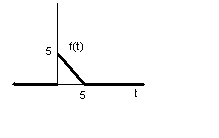
Отже .

Операторне рівняння має наступний вигляд:

За теоремою запізнення:

БІЛЕТ № 11.

1. Розвинути в ряд Фур’є за косинусами функцію

Продовжимо дану функцію парним чином та побудуємо графік суми ряду:

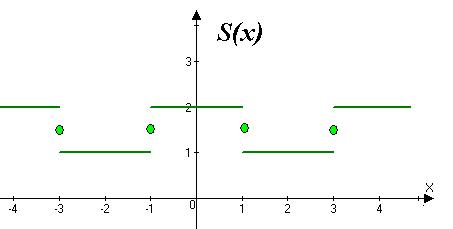
Сума ряду в точках розриву: .

Коефіцієнти розкладу:

.

Розклад в ряд Фур’є по косинусах для даної функції має вид:

, де .

2. За допомогою лишків обчислити контурний інтеграл:

, якщо с: .

.

Будуємо область інтегрування:

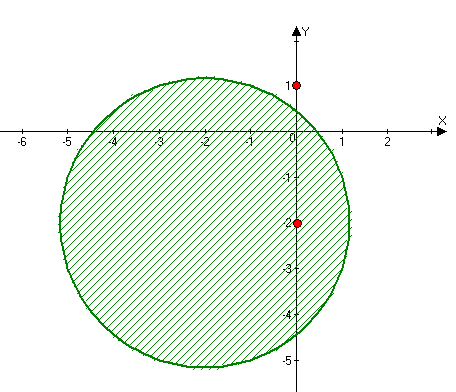
Маємо дві особливі точки та , які є полюсами п’ятого порядку. Особлива точка не належить області інтегрування.

.

Відповідь: .

3. Розв’язати задачу Коші операційним методом

y′′ + 9y = f(t); y(0) = y′(0) = 0;

.

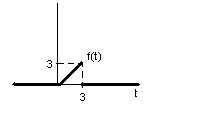
Отже .

Операторне рівняння має наступний вигляд:

За теоремою запізнення:

БІЛЕТ № 12.

1. Розвинути в ряд Фур’є за синусами функцію

Продовжимо дану функцію непарним чином та побудуємо графік суми ряду:

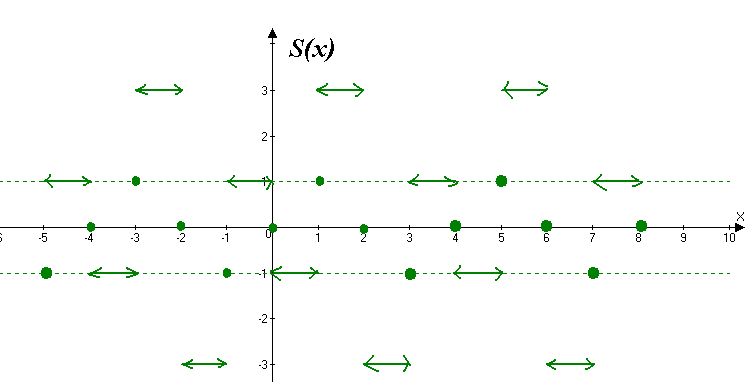
Сума ряду в точках розриву: ,

Коефіцієнти розкладу:

Розклад в ряд Фур’є по синусах для даної функції має вид:

, де .

2. За допомогою лишків обчислити контурний інтеграл:

, якщо с: .

, будуємо область інтегрування:

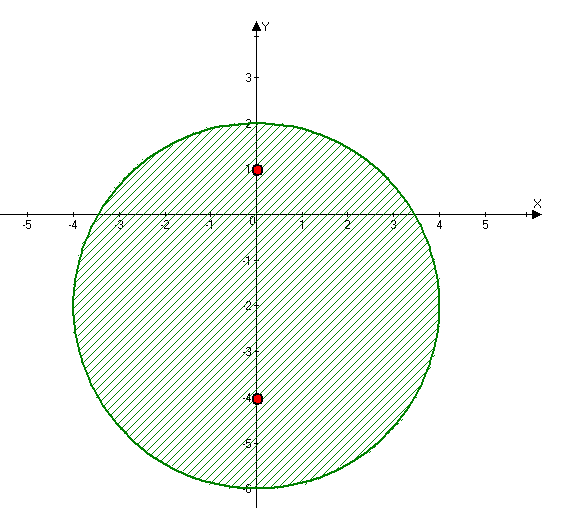
Маємо дві особливі точки , - полюс 5-го порядку, , - полюс 6-го порядку. Знайдемо відповідні лишки в даних особливих точках:

Відповідь: 0.

3. Розв’язати задачу Коші операційним методом

y′′ + 64y = f(t); y(0) = y′(0) = 0;

.

Отже

Операторне рівняння має наступний вигляд:

За теоремою запізнення:

БІЛЕТ № 13.

1. Знайти область збіжності ряду

.

1) Знайдемо радіус збіжності даного ряду:

2) Визначимо область збіжності ряду: .

Розглянемо поведінку ряду в граничних точках. При ми отримаємо знакозмінний ряд , який є умовно збіжним рядом Лейбніца:

• , - знаки членів ряду чергуються.

• , - модулі ряду утворюють монотонно спадну послідовність.

• .

При отримаємо розбіжний ряд з додатними членами . Ряд є розбіжним за граничною ознакою порівняння з розбіжним рядом Діріхлє при степені , тобто : , тобто ряди та одночасно розбіжні.

Відповідь: , - область збіжності ряду.

2. За допомогою лишків обчислити контурний інтеграл:

, якщо с: .

, будуємо область інтегрування:

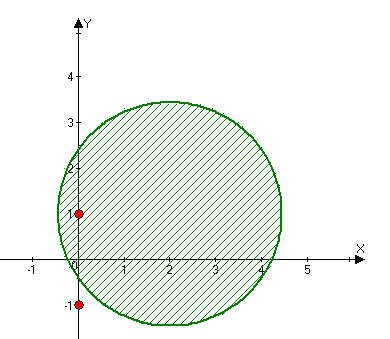
Ми маємо дві особливі точки, які є полюсами 2-го порядку: та . Але точка не належить області інтегрування. Лишок по особливій точці має вид:

Відповідь: .

3. Розв’язати задачу Коші операційним методом

y′′ - 16y′ = f(t); y(0) = y′(0) = 0;

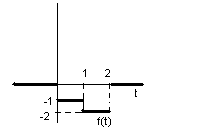
при умові .

.

Отже

Операторне рівняння має наступний вигляд:

За теоремою запізнення:

БІЛЕТ № 14.

1. Розвинути в ряд Фур’є за косинусами функцію

, .

Продовжимо функцію парним чином та побудуємо графік суми ряду:

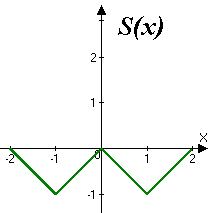
Дана функція є кусково неперервною та кусково диференційованою, тобто задовольняє умовам теореми Діріхлє.

Коефіцієнти розкладу:

.

Розклад за косинусами в ряд Фур’є має вигляд:

, де .