
- •1) Физика — фундаментальная отрасль естествознания
- •2) Предмет и задачи физики
- •Абсолютная система отсчёта
- •Физическая размерность
- •Энергия и масса
- •Теорема о кинетической энергии
- •48) Уравнение неразрывности
- •61) Энергия в релятивистской механике -
- •Второй закон Ньютона в релятивистской механике
- •Существуют также шкала Фаренгейта, Цельсия , Кельвина
- •Шкала Фаренгейта
- •Закон теплопроводности Фурье
- •Прибор для измерения вязкости называется вискозиметром. Влияние температуры на вязкость газов
- •Принцип суперпозиции в электродинамике
- •Примеры нарушения электродинамического принципа суперпозиции
- •Отсутствие принципа суперпозиции в нелинейных теориях
- •Вычисление разности потенциалов по напряженности поля
- •1.6. Электрическое поле диполя
- •Квантовая механика Полупроводники Физика атомного ядра
- •Поляризация диэлектриков
- •Индуцированный заряд
- •Как обнаружить электрический заряд?
- •Как определить знак электрического заряда?
- •Электростатическая индукция в проводниках
- •Электростатическая индукция в диэлектриках
- •Применение
Существуют также шкала Фаренгейта, Цельсия , Кельвина
и некоторые другие.
Шкала Фаренгейта
Основная статья: Градус Фаренгейта
В Англии и, в особенности, в США используется шкала Фаренгейта. Ноль градусов Цельсия — это 32 градуса Фаренгейта, а 100 градусов Цельсия — 212 градуса Фаренгейта.
В настоящее время принято следующее определение шкалы Фаренгейта: это температурная шкала, 1 градус которой (1 °F) равен 1/180 разности температур кипения воды и таяния льда при атмосферном давлении, а точка таяния льда имеет температуру +32 °F. Температура по шкале Фаренгейта связана с температурой по шкале Цельсия (t °С) соотношением t °С = 5/9 (t °F — 32), t °F = 9/5 t °С + 32. Предложена Г. Фаренгейтом в 1724 году.
Термодинамическая температурная шкала
ТЕРМОДИНАМИ́ЧЕСКАЯ ТЕМПЕРАТУ́РНАЯ ШКАЛА́ (Кельвина шкала), абсолютная шкала температур, не зависящая от свойств термометрического вещества (начало отсчета — абсолютный нуль температуры). Построение термодинамической температурной шкалы основано на втором начале термодинамики и, в частности, на независимости кпд Карно цикла от природы рабочего тела. Единица термодинамической температуры — кельвин(К) — определяется как 1/273,16 часть термодинамической температуры тройной точки воды.
Термодинамический процесс.
Тепловой процесс (термодинамический процесс) — изменение макроскопического состояния термодинамической системы.
Система, в которой идёт тепловой процесс, называется рабочим телом.
Тепловые процессы можно разделить на равновесные и неравновесные. Равновесным называется процесс, при котором все состояния, через которые проходит система, являются равновесными состояниями.
Тепловые процессы можно разделить на обратимые и необратимые. Обратимым называется процесс, который можно провести в противоположном направлении через все те же самые промежуточные состояния.
Можно выделить несколько простых, но широко распространённых на практике, тепловых процессов:
Адиабатный процесс — происходящий без теплообмена с окружающей средой;
Изохорный процесс — происходящий при постоянном объёме;
Изобарный процесс — происходящий при постоянном давлении;
Изотермический процесс — происходящий при постоянной температуре;
Изоэнтропийный процесс — происходящий при постоянной энтропии;
Изоэнтальпийный процесс — происходящий при постоянной энтальпии;
Политропный процесс — происходящий при постоянной теплоёмкости;
Термодинамическое равновесие.
Термодинамическое равновесие — состояние системы, при котором остаются неизменными по времени макроскопические величины этой системы (температура, давление, объём,энтропия) в условиях изолированности от окружающей среды. В общем, эти величины не являются постоянными, они лишь флуктуируют (колеблются) возле своих средних значений. Если равновесной системе соответствует несколько состояний, в каждом из которых система может находиться неопределенно долго, то о системе говорят, что она находится в метастабильном равновесии. В состоянии равновесия в системе отсутствуют потоки материи или энергии, неравновесные потенциалы (или движущие силы), изменения количества присутствующих фаз. Отличают тепловое, механическое, радиационное (лучистое) и химическое равновесия. На практике условие изолированности означает, что процессыустановления равновесия протекают гораздо быстрее, чем происходят изменения на границах системы (то есть изменения внешних по отношению к системе условий), и осуществляется обмен системы с окружением веществом и энергией. Иными словами, термодинамическое равновесие достигается, если скорость релаксационных процессов достаточно велика (как правило, это характерно для высокотемпературных процессов) либо велико время для достижения равновесия (этот случай имеет место в геологических процессах).
В реальных процессах часто реализуется неполное равновесие, однако степень этой неполноты может быть существенной и несущественной. При этом возможны три варианта:
равновесие достигается в какой-либо части (или частях) относительно большой по размерам системы — локальное равновесие,
неполное равновесие достигается вследствие разности скоростей релаксационных процессов, протекающих в системе — частичное равновесие,
имеют место как локальное, так и частичное равновесие.
В неравновесных системах происходят изменения потоков материи или энергии, или, например, фаз.
Идеальный газ.
Идеальный газ — математическая модель газа, в которой предполагается, что потенциальной энергией взаимодействия молекул можно пренебречь по сравнению с их кинетической энергией. Между молекулами не действуют силы притяжения или отталкивания, соударения частиц между собой и со стенками сосуда абсолютно упруги, а время взаимодействия между молекулами пренебрежимо мало по сравнению со средним временем между столкновениями. В расширенной модели идеального газа частицы, из которого он состоит, имеют также форму в виде упругих сфер или эллипсоидов, что позволяет учитывать энергию не только поступательного, но и вращательно-колебательного движения, а также не только центральные, но и нецентральные столкновения частиц и др.[1].
Модель широко применяется для решения задач термодинамики газов и задач аэрогазодинамики. Например, воздух при атмосферном давлении икомнатной температуре с большой точностью описывается данной моделью. В случае экстремальных температур или давлений требуется применение более точной модели, например модели газа Ван-дер-Ваальса, в котором учитывается притяжение между молекулами.
Различают классический идеальный газ (его свойства выводятся из законов классической механики и описываются статистикой Больцмана) и квантовый идеальный газ (свойства определяются законами квантовой механики, описываются статистиками Ферми — Дирака или Бозе — Эйнштейна). Свойства идеального газа на основе молекулярно-кинетических представлений определяются исходя из физической модели идеального газа, в которой приняты следующие допущения:
Диаметр молекулы
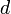 пренебрежимо
мал по сравнению со средним расстоянием
между ними (
пренебрежимо
мал по сравнению со средним расстоянием
между ними (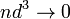 ) [7][8].
) [7][8].Импульс передается только при соударениях, то есть, силы притяжения между молекулами не учитываются, а силы отталкивания возникают только при соударениях.
Суммарная энергия частиц газа постоянна если нет передачи тепла или совершения газом работы.
В этом случае частицы газа движутся независимо друг от друга, давление газа на стенку равно сумме импульсов в единицу времени, переданной при столкновении частиц со стенкой, энергия — сумме энергий частиц газа.
По эквивалентной формулировке идеальный газ - такой газ, который одновременно подчиняется закону Бойля — Мариотта и Гей-Люссака[8], то есть:
![]()
где ![]() —
давление,
—
давление, ![]() —
абсолютная температура. Свойства
идеального газа описываются уравнением
Менделеева — Клапейрона
—
абсолютная температура. Свойства
идеального газа описываются уравнением
Менделеева — Клапейрона
![]() ,
,
где
- универсальная
газовая постоянная,
—
масса, ![]() — молярная
масса.
— молярная
масса.
или
![]()
где ![]() — концентрация
частиц,
— концентрация
частиц, ![]() — постоянная
Больцмана.
— постоянная
Больцмана.
Для любого идеального газа справедливо соотношение Майера:
![]()
где ![]() — универсальная
газовая постоянная,
— универсальная
газовая постоянная, ![]() —
молярная теплоемкость при
постоянном давлении,
—
молярная теплоемкость при
постоянном давлении, ![]() —
молярная теплоемкость при постоянном
объёме.
—
молярная теплоемкость при постоянном
объёме.
распределение Больцмана:
![]()
где ![]() —
среднее число частиц, находящихся в
—
среднее число частиц, находящихся в ![]() -ом
состоянии с энергией
-ом
состоянии с энергией ![]() ,
а константа
,
а константа ![]() определяется
условием нормировки:
определяется
условием нормировки:
![]()
где ![]() —
полное число частиц.
—
полное число частиц.
Распределение Больцмана является предельным случаем (квантовые эффекты пренебрежимо малы) распределений Ферми — Дирака и Бозе — Эйнштейна, и, соответственно, классический идеальный газ является предельным случаем Ферми-газа и Бозе-газа.
Опытные законы идеальных газов.
Изопроцессы идеального газа – процессы, при которых один из параметров остаётся неизменным.
1. Изохорический процесс. Закон Шарля. V = const.
Изохорическим процессом называется процесс, протекающий при постоянном объёме V. Поведение газа при этом изохорическом процессе подчиняется закону Шарля:
При постоянном объёме и неизменных значениях массы газа и его молярной массы, отношение давления газа к его абсолютной температуре остаётся постоянным: P/Т = const.
График изохорического процесса на РV-диаграмме называется изохорой. Полезно знать график изохорического процесса на РТ- и VT-диаграммах (рис. 1.6). Уравнение изохоры:
|
|
|
(1.4.1) |
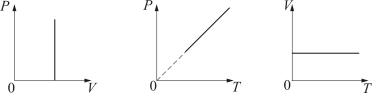 Рис.
1.6
Рис.
1.6
Если температура газа выражена в градусах Цельсия, то уравнение изохорического процесса записывается в виде
|
|
|
(1.4.2) |
где Р0 – давление при 0 °С, α - температурный коэффициент давления газа равный 1/273 град-1. График такой зависимости на Рt-диаграмме имеет вид, показанный на рисунке 1.7.
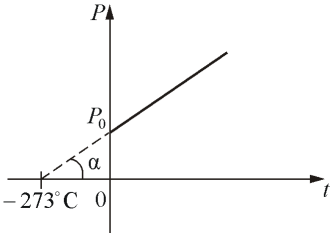 Рис.
1.7
Рис.
1.7
2. Изобарический процесс. Закон Гей-Люссака. Р = const.
Изобарическим процессом называется процесс, протекающий при постоянном давлении Р. Поведение газа при изобарическом процессе подчиняется закону Гей-Люссака:
При постоянном давлении и неизменных значениях массы и газа и его молярной массы, отношение объёма газа к его абсолютной температуре остаётся постоянным: V/T = const.
График изобарического процесса на VT-диаграмме называется изобарой. Полезно знать графики изобарического процесса на РV- и РT-диаграммах (рис. 1.8).
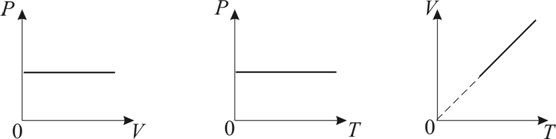 Рис.
1.8
Рис.
1.8
Уравнение изобары:
|
|
|
(1.4.3) |
Если температура газа выражена в градусах Цельсия, то уравнение изобарического процесса записывается в виде
|
|
|
(1.4.4) |
где α =1/273 град -1- температурный коэффициент объёмного расширения. График такой зависимости на Vt диаграмме имеет вид, показанный на рисунке 1.9.
 Рис.
1.9
Рис.
1.9
3. Изотермический процесс. Закон Бойля – Мариотта. T = const.
Изотермическим процессом называется процесс, протекающий при постоянной температуре Т.
Поведение идеального газа при изотермическом процессе подчиняется закону Бойля – Мариотта:
При постоянной температуре и неизменных значениях массы газа и его молярной массы, произведение объёма газа на его давление остаётся постоянным: PV = const.
График изотермического процесса на РV-диаграмме называется изотермой. Полезно знать графики изотермического процесса на VT- и РT-диаграммах (рис. 1.10).
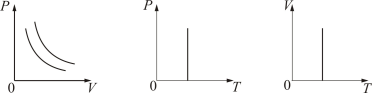 Рис.
1.10
Рис.
1.10
Уравнение изотермы:
|
|
|
(1.4.5) |
4. Адиабатический процесс (изоэнтропийный):
Адиабатический процесс – термодинамический процесс, происходящий без теплообмена с окружающей средой.
5. Политропический процесс. Процесс, при котором теплоёмкость газа остаётся постоянной. Политропический процесс – общий случай всех перечисленных выше процессов.
6. Закон Авогадро. При одинаковых давлениях и одинаковых температурах, в равных объёмах различных идеальных газов содержится одинаковое число молекул. В одном моле различных веществ содержится NA=6,02·1023молекул (число Авогадро).
7. Закон Дальтона. Давление смеси идеальных газов равно сумме парциальных давлений Р, входящих в неё газов:
|
|
|
(1.4.6) |
Парциальное давление Pn – давление, которое оказывал бы данный газ, если бы он один занимал весь объем.
При ![]() ,
давление смеси газов:
,
давление смеси газов:
|
|
|
(1.4.7) |
8. Объединённый газовый закон (Закон Клапейрона).
В соответствии с законами Бойля – Мариотта (1.4.5) и Гей-Люссака (1.4.3) можно сделать заключение, что для данной массы газа
|
|
|
(1.4.8) |
Уравнение Клапейрона-Менделеева.
Газы нередко бывают реагентами и продуктами в химических реакциях. Не всегда удается заставить их реагировать между собой при нормальных условиях. Поэтому нужно научиться определять число молей газов в условиях, отличных от нормальных.
Для этого используют уравнение состояния идеального газа (его также называют уравнением Клапейрона-Менделеева):
PV = nRT
где n – число молей газа;
P – давление газа (например, в атм;
V – объем газа (в литрах);
T – температура газа (в кельвинах);
R – газовая постоянная (0,0821 л·атм/моль·K).
Из газового закона найдем искомое число молей n:



Очевидно, что уравнение Клапейрона-Менделеева одинаково справедливо как для начального состояния газа, так и для конечного:
P1V1 = nRT1
P2V2 = nRT2
Если теперь почленно разделить верхнее уравнение на нижнее, то при неизменном числе молей n мы получаем:

Отсюда:
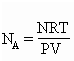
Основное уравнение МКТ идеальных газов.

Опытное обоснование МКТ.
Молекулярно-кинетическая теория (сокращённо МКТ) — теория XIX века, рассматривавшая строение вещества, в основном газов, с точки зрения трёх основных приближенно верных положений: - все тела состоят из частиц, размером которых можно пренебречь: атомов, молекул и ионов; - частицы находятся в непрерывном хаотическом движении (тепловом); - частицы взаимодействуют друг с другом путём абсолютно упругих столкновений. Основными доказательствами этих положений считались: - Диффузия - Броуновское движение - Изменение агрегатных состояний вещества
Броуновское движение.
Бро́уновское движе́ние —беспорядочное движение микроскопических видимых, взвешенных в жидкости или газе частиц твердого вещества, вызываемого тепловым движением частиц жидкости или газа. Броуновское движение никогда не прекращается. Броуновское движение связано с тепловым движением, но не следует смешивать эти понятия. Броуновское движение является следствием и свидетельством существования теплового движения.
формула для коэффициента диффузии сферических броуновских частиц[3]:
![]()
где ![]() — коэффициент
диффузии,
— универсальная
газовая постоянная,
— коэффициент
диффузии,
— универсальная
газовая постоянная, ![]() — абсолютная
температура,
— абсолютная
температура, ![]() — постоянная
Авогадро,
— постоянная
Авогадро, ![]() —
радиус частиц,
—
радиус частиц, ![]() — динамическая
вязкость.
— динамическая
вязкость.
Закон Максвелла о распределении молекул идеального газа по скоростям и энергиям теплового движения. Если разбить диапазон скоростей молекул на малые интервалы, которые равны dν, то на каждый интервал скорости приходится число молекул dN(ν), имеющих скорость, которая заключена в этом интервале. Функция f(ν) задает относительное число молекул dN(ν)/N, скорости которых находятся в интервале от ν до ν+dν, т. е.
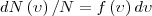 откуда
откуда
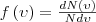 Применяя
методы теории вероятностей, Максвелл
получил функцию f(ν)
— закон
о распределеня молекул идеального газа
по скоростям:
Применяя
методы теории вероятностей, Максвелл
получил функцию f(ν)
— закон
о распределеня молекул идеального газа
по скоростям:
 видно,
что конкретный вид функции зависит от
вида газа (от массы молекулы) и от
параметра состояния (от температуры
Т).
видно,
что конкретный вид функции зависит от
вида газа (от массы молекулы) и от
параметра состояния (от температуры
Т).
![]() найдем
распределение молекул газа по значениям
кинетической энергии ε. С этой целью
перейдем от переменной ν к
переменной ε=m0v2/2.
Подставив в
найдем
распределение молекул газа по значениям
кинетической энергии ε. С этой целью
перейдем от переменной ν к
переменной ε=m0v2/2.
Подставив в
![]() и
и ![]() ,
получим
,
получим
![]() где
dN(ε) — число молекул, которые имели
кинетическую энергию поступательного
движения, заключенную в интервале от ε
до ε + dε.
Значит, функция
распределения молекул по энергиям
теплового движения
где
dN(ε) — число молекул, которые имели
кинетическую энергию поступательного
движения, заключенную в интервале от ε
до ε + dε.
Значит, функция
распределения молекул по энергиям
теплового движения
![]()
Барометрическая формула.
Барометрическая формула — зависимость давления или плотности газа от высоты в поле тяжести.
Для идеального
газа,
имеющего постоянную температуру
и
находящегося в однородном поле тяжести
(во всех точках его объёма ускорение
свободного падения ![]() одинаково),
барометрическая формула имеет следующий
вид:
одинаково),
барометрическая формула имеет следующий
вид:

где ![]() —
давление газа в слое, расположенном на
высоте
—
давление газа в слое, расположенном на
высоте ![]() ,
, ![]() —
давление на нулевом уровне (
—
давление на нулевом уровне (![]() ),
), ![]() — молярная
масса газа,
— газовая
постоянная,
— абсолютная
температура.
Из барометрической формулы следует,
что концентрация молекул
— молярная
масса газа,
— газовая
постоянная,
— абсолютная
температура.
Из барометрической формулы следует,
что концентрация молекул ![]() (или
плотность газа) убывает с высотой по
тому же закону:
(или
плотность газа) убывает с высотой по
тому же закону:
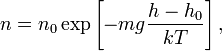
где
—
масса молекулы газа, ![]() — постоянная
Больцмана.
— постоянная
Больцмана.
Распределение Больцмана.
Распределение Больцмана – распределение по энергиям частиц (атомов, молекул) идеального газа в условиях термодинамического равновесия было открыто в 1868–1871 гг. австрийским физиком Л. Больцманом.
В присутствии гравитационного поля (или, в общем случае, любого потенциального поля) на молекулы газа действует сила тяжести. В результате, концентрация молекул газа оказывается зависящей от высоты:
|
где n – концентрация молекул на высоте h, n0 – концентрация молекул на начальном уровне h = 0, m – масса частиц, g – ускорение свободного падения, k – постоянная Больцмана, T – температура.
Опыт Штерна.
Опыт
Штерна —
опыт, впервые проведённый немецким физиком Отто
Штерном в 1920 году.
Опыт являлся одним из первых практических
доказательств состоятельности
молекулярно-кинетической теории строения
вещества. В нём были непосредственно
измерены скорости теплового движения
молекул и подтверждено наличие распределения
молекул газов по скоростям.
![]() ,
,
где s — смещение полосы, l — расстояние между цилиндрами, а u — скорость движения точек внешнего цилиндра.
Опыт Ламмерта.
Опыт
Ламмерта (1929)
был проведён для подтверждения распределения
Максвелла.
внутри
ящика находится газ, молекулы которого
вылетают через отверстие наружу. Диаметр
отверстия много меньше длины свободного
пробега молекул, молекул в ящике много,
так что исчезновение вылетающих не
меняет имеющееся распределение по
скоростям внутри ящика. Колеса селектора,
на поверхности которых находятся
выступы, пропускающие или останавливающие
летящие молекулы, вращаются с угловой
скоростью
.
Так, преодолев первое колесо, молекула
летит расстояние
до
второго, которое за это время поворачивается
на угол ![]() .
Выполняется соотношение
.
Выполняется соотношение
![]()
Так,
регулируя
,
и
,
можно пропускать только молекулы с
определенной скоростью ![]() .
Пролетевшие через второе колесо молекулы
оставляют след на пластине. Проведя
эксперимент для различных значений
,
можно получить экспериментальную
картину распределения скоростей в
исследуемом газе. Так, с помощью этого
эксперимента (в числе прочих) было
подтверждено распределение Максвелла.
.
Пролетевшие через второе колесо молекулы
оставляют след на пластине. Проведя
эксперимент для различных значений
,
можно получить экспериментальную
картину распределения скоростей в
исследуемом газе. Так, с помощью этого
эксперимента (в числе прочих) было
подтверждено распределение Максвелла.
Явления переноса в термодинамически неравновесных системах.
В
термодинамически неравновесных системах
происходят особые необратимые процессы,
называемые явлениями
переноса,
в результате которых осуществляется
пространственный перенос массы, импульса,
энергии. К явлениям переноса
относятсятеплопроводность (перенос
энергии), диффузия (перенос
массы) и внутреннее
трение (перенос
импульса). Ограничимся одномерными
явлениями переноса. Систему отсчета
будем выберать так, чтобы ось х была
направлена в сторону в направления
переноса.
1. Теплопроводность.
Если в первой области газа средняя
кинетическая энергия молекул больше,
чем во второй, то вследствие постоянных
столкновений молекул с течением времени
происходит процесс выравнивания средних
кинетических энергий молекул, т. е.,
выравнивание температур. Перенос энергии
в форме теплоты подчиняется закону
Фурье:
![]() (1)
где
jE — плотность
теплового потока —
величина, которая определяется энергией,
переносимой в форме теплоты в единицу
времени через единичную площадку,
перпендикулярную оси х, λ — теплопроводность,
— градиент температуры, равный скорости
изменения температуры на единицу длины
х в направлении нормали к этой площадке.
Знак минус говорит о том, что во время
теплопроводности энергия перемещается
в направлении убывания температуры
(поэтому знаки jE и
– противоположны). Теплопроводность λ
равна плотности теплового потока при
градиенте температуры, равном
единице.
Можно
показать, что
(1)
где
jE — плотность
теплового потока —
величина, которая определяется энергией,
переносимой в форме теплоты в единицу
времени через единичную площадку,
перпендикулярную оси х, λ — теплопроводность,
— градиент температуры, равный скорости
изменения температуры на единицу длины
х в направлении нормали к этой площадке.
Знак минус говорит о том, что во время
теплопроводности энергия перемещается
в направлении убывания температуры
(поэтому знаки jE и
– противоположны). Теплопроводность λ
равна плотности теплового потока при
градиенте температуры, равном
единице.
Можно
показать, что
![]() (2)
где
сV — удельная
теплоемкость газа
при постоянном ρ — плотность газа, <ν>
— средняя скорость теплового движения
молекул, <l>
— средняя длина свободного
пробега.
2. Диффузия.;
диффузия есть обмен масс частиц этих
тел
Явление
диффузии для химически однородного
газа подчиняется закону
Фика:
(2)
где
сV — удельная
теплоемкость газа
при постоянном ρ — плотность газа, <ν>
— средняя скорость теплового движения
молекул, <l>
— средняя длина свободного
пробега.
2. Диффузия.;
диффузия есть обмен масс частиц этих
тел
Явление
диффузии для химически однородного
газа подчиняется закону
Фика:
![]() (3)
где
jm — плотность
потока массы
(3)
где
jm — плотность
потока массы
D — диффузия (коэффициент диффузии), dρ/dx — градиент плотности, который равен скорости изменения плотности на единицу длины х в направлении нормали к этой площадке. Диффузия D численно равна плотности потока массы при градиенте плотности, равном единице.
Согласно
кинетической теории газов,
![]() (4)
3. Внутреннее
трение (вязкость)
Как
известно, сила внутреннего трения между
двумя слоями газа (жидкости)
подчиняется закону
Ньютона:
(4)
3. Внутреннее
трение (вязкость)
Как
известно, сила внутреннего трения между
двумя слоями газа (жидкости)
подчиняется закону
Ньютона:
![]() (5)
где
η — динамическая вязкость (вязкость),
dν/dx
— градиент скорости S — площадь.
Согласно
второму закону Ньютона взаимодействие
двух слоев можно рассматривать как
процесс, при котором в единицу времени
от одного слоя к другому передается
импульс, который по модулю равен
действующей силе. Тогда выражение можно
записать в виде
(5)
где
η — динамическая вязкость (вязкость),
dν/dx
— градиент скорости S — площадь.
Согласно
второму закону Ньютона взаимодействие
двух слоев можно рассматривать как
процесс, при котором в единицу времени
от одного слоя к другому передается
импульс, который по модулю равен
действующей силе. Тогда выражение можно
записать в виде
![]() где
jp — плотность
потока импульса —
величина, которая определяется
определяемая полным импульсом
где
jp — плотность
потока импульса —
величина, которая определяется
определяемая полным импульсом
dν/dx
— градиент скорости
Динамическая
вязкость η
численно равна плотности потока импульса
при градиенте скорости, равном единице;
она вычисляется по формуле
![]() (7)
Из
сопосавления формул которые описывают
явления переноса, следует, что
закономерности всех явлений переноса
сходны между собой.
Рассмотренные
законы Фурье, Фика и Ньютона не вскрывают
молекулярно-кинетической сути
коэффициентов λ, D и η.(1,3,6) Выражения для
коэффициентов переноса получаются из
кинетической теории. Они записаны без
вывода, поскольку строгое и формальное
рассмотрение явлений переноса довольно
громоздко, а качественное — не имеет
смысла. Формулы
(7)
Из
сопосавления формул которые описывают
явления переноса, следует, что
закономерности всех явлений переноса
сходны между собой.
Рассмотренные
законы Фурье, Фика и Ньютона не вскрывают
молекулярно-кинетической сути
коэффициентов λ, D и η.(1,3,6) Выражения для
коэффициентов переноса получаются из
кинетической теории. Они записаны без
вывода, поскольку строгое и формальное
рассмотрение явлений переноса довольно
громоздко, а качественное — не имеет
смысла. Формулы
Из
этих формул(2,4,7) следуют простые
зависимости между λ, D и η:
![]() и
и ![]()
Теплопроводность.
Теплопрово́дность — это процесс переноса внутренней энергии от более нагретых частей тела (или тел) к менее нагретым частям (или телам), осуществляемый хаотически движущимися частицами тела (атомами, молекулами, электронами и т. п.). Такой теплообмен может происходить в любых телах с неоднородным распределением температур, но механизм переноса теплоты будет зависеть от агрегатного состояния вещества.


