Физическая размерность
Энергия E имеет размерность, равную:
Описание |
Формула |
Силе, умноженной на длину |
E ~ F·l |
Давлению, умноженному на объём |
E ~ P·V |
Импульсу, умноженному на скорость |
E ~ p·v |
Массе, умноженной на квадрат скорости |
E ~ m·v² |
Заряду, умноженному на напряжение |
E ~ q·U |
Мощности, умноженной на время |
E ~ N·t |
Энергия и масса
Основная статья: Эквивалентность массы и энергии
Согласно специальной теории относительности между массой и энергией существует связь, выражаемая знаменитой формулой Эйнштейна
где E — энергия системы, m — её масса, c — скорость света. Несмотря на то, что исторически предпринимались попытки трактовать это выражение как полную эквивалентность понятия энергии и массы, что, в частности, привело к появлению такого понятия как релятивистская масса, в современной физике принято сужать смысл этого уравнения, понимая под массой массу тела в состоянии покоя (так называемая масса покоя), а под энергией — только внутреннюю энергию, заключённую в системе.
Энергия
тела, согласно законам классической
механики, зависит от системы отсчета,
то есть неодинакова для разных
наблюдателей. Если тело движется со
скоростью v относительно некоего
наблюдателя, то для другого наблюдателя,
движущегося с той же скоростью, оно
будет казаться неподвижным. Соответственно,
для первого наблюдателя кинетическая
энергия тела
будет равна, 
,
где m — масса тела, а для другого
наблюдателя — нулю.
Эта зависимость энергии от системы отсчета сохраняется также в теории относительности. Для определения преобразований, происходящих с энергией при переходе от одной инерциальной системы отсчета к другой используется сложная математическая конструкция — тензор энергии-импульса.
Зависимость энергии тела от скорости рассматривается уже не так, как в ньютоновской физике, а согласно вышеназванной формуле Эйнштейна:
,
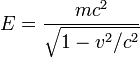где — инвариантная масса. В системе отсчета, связанной с телом, его скорость равна нулю, а энергия, которую называют энергией покоя, выражается формулой:
.
Это минимальная энергия, которую может иметь массивное тело. Значение формулы Эйнштейна также в том, что до неё энергия определялась с точностью до произвольной постоянной, а формула Эйнштейна находит абсолютное значение этой постоянной.
38) Работа – в лекции
Работа есть физическая величина, численно равная произведению силы на перемещение в направлении действия этой силы и ей же вызванное. Соответственно формула A = F*s. Если перемещение по направлению не совпадает с направлением действия силы, то появляется косинус угла.
При прямолинейном движении одной материальной точки и постоянном значении приложенной к ней силы работа (этой силы) равна произведению величины проекции вектора силы на направление движения и величины совершённого перемещения[3]:
Здесь
точкой обозначено скалярное
произведение[4], 
— вектор
перемещения;
подразумевается, что действующая
сила
постоянна
в течение всего того времени, за которое
вычисляется работа.
Если сила не постоянна, то в этом случае она вычисляется как интеграл[5]:
(подразумевается
суммирование по кривой, которая является
пределом ломаной, составленной из
последовательных перемещений 
если
вначале считать их конечными, а потом
устремить длину каждого к нулю).
Если существует зависимость силы от координат[6], интеграл определяется[7] следующим образом:
,
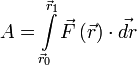где 
и 
— радиус-векторы начального
и конечного положения тела соответственно.
39) Мощность
Мо́щность — физическая величина, равная в общем случае скорости изменения энергии системы. В более узком смысле мощность равна отношениюработы, выполняемой за некоторый промежуток времени, к этому промежутку времени.
Различают
среднюю мощность за промежуток времени 
и мгновенную мощность в данный момент времени:
Интеграл от мгновенной мощности за промежуток времени равен полной переданной энергии за это время:
Если на движущееся тело действует сила, то эта сила совершает работу. Мощность в этом случае равна скалярному произведению вектора силы на вектор скорости, с которой движется тело:
|
|
где F —
сила, v —
скорость, 
—
угол между вектором скорости и силы.
Частный случай мощности при вращательном движении:
|
|
M —
момент силы, 
—
угловая скорость, 
—
число пи, n —
частота вращения (число оборотов в
минуту, об/мин.).
40) Кинетическая энергия
Кинети́ческая эне́ргия — энергия механической системы, зависящая от скоростей движения её точек. Часто выделяют кинетическую энергию поступательного и вращательного движения. Единица измерения в системе СИ — Джоуль.
Более строго, кинетическая энергия есть разность между полной энергией системы и её энергией покоя; таким образом, кинетическая энергия — часть полной энергии, обусловленная движением.
Рассмотрим систему, состоящую из одной частицы, и запишем уравнение движения:
—
есть
результирующая всех сил,
действующих на тело. Скалярно
умножим уравнение
на перемещениечастицы 
.
Учитывая, что 
,
Получим:
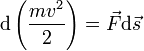
Если система
замкнута,
то есть 
,
то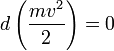 
,
а величина
остаётся постоянной. Эта величина называется кинетической энергией частицы. Если система изолирована, то кинетическая энергия является интегралом движения.
Для абсолютно твёрдого тела полную кинетическую энергию можно записать в виде суммы кинетической энергии поступательного и вращательного движения:
где:
—
масса
тела
—
скорость центра
масс тела
— момент
инерции тела
— угловая
скорость тела.
41) Теорема о кинетической энергии