- •1) Физика — фундаментальная отрасль естествознания
- •2) Предмет и задачи физики
- •Абсолютная система отсчёта
- •Физическая размерность
- •Энергия и масса
- •Теорема о кинетической энергии
- •48) Уравнение неразрывности
- •61) Энергия в релятивистской механике -
- •Второй закон Ньютона в релятивистской механике
- •Существуют также шкала Фаренгейта, Цельсия , Кельвина
- •Шкала Фаренгейта
- •Закон теплопроводности Фурье
- •Прибор для измерения вязкости называется вискозиметром. Влияние температуры на вязкость газов
- •Принцип суперпозиции в электродинамике
- •Примеры нарушения электродинамического принципа суперпозиции
- •Отсутствие принципа суперпозиции в нелинейных теориях
- •Вычисление разности потенциалов по напряженности поля
- •1.6. Электрическое поле диполя
- •Квантовая механика Полупроводники Физика атомного ядра
- •Поляризация диэлектриков
- •Индуцированный заряд
- •Как обнаружить электрический заряд?
- •Как определить знак электрического заряда?
- •Электростатическая индукция в проводниках
- •Электростатическая индукция в диэлектриках
- •Применение
Поляризация диэлектриков
Материал из Википедии — свободной энциклопедии
Перейти к: навигация, поиск
У этого термина существуют и другие значения, см. Поляризация.
Поляризация диэлектриков — явление, связанное с ограниченным смещением связанных зарядов в диэлектрике или поворотом электрических диполей, обычно под воздействием внешнего электрического поля, иногда под действием других внешних сил или спонтанно.
Поляризацию диэлектриков характеризует вектор электрической поляризации. Физический смысл вектора электрической поляризации — это дипольный момент, отнесенный к единице объема диэлектрика. Иногда вектор поляризации коротко называют просто поляризацией.
Вектор поляризации применим для описания макроскопического состояния поляризации не только обычных диэлектриков, но и сегнетоэлектриков, и, в принципе, любых сред, обладающих сходными свойствами. Он применим не только для описания индуцированной поляризации, но и спонтанной поляризации (у сегнетоэлектриков).
Поляризация — состояние диэлектрика, которое характеризуется наличием электрического дипольного момента у любого (или почти любого) элемента его объема.
Различают поляризацию, наведенную в диэлектрике под действием внешнего электрического поля, и спонтанную (самопроизвольную) поляризацию, которая возникает в сегнетоэлектриках в отсутствие внешнего поля. В некоторых случаях поляризация диэлектрика (сегнетоэлектрика) происходит под действием механических напряжений, сил трения или вследствие изменения температуры.
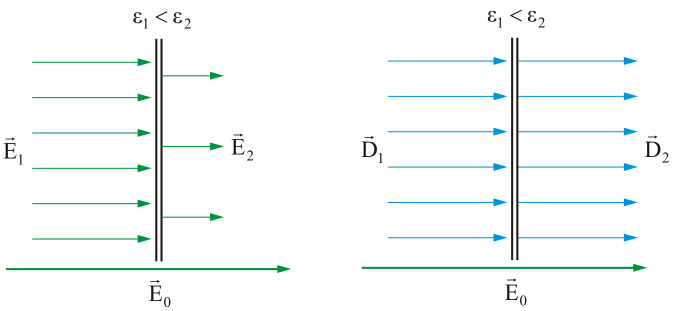
Поляризация не изменяет суммарного заряда в любом макроскопическом объеме внутри однородного диэлектрика. Однако она сопровождается появлением на его поверхности связанных электрических зарядов с некоторой поверхностной плотностью σ. Эти связанные заряды создают в диэлектрике дополнительное макроскопическое поле с напряженностью Е1, направленное против внешнего поля с напряженностью Е0. Результирующая напряженность поля Е внутри диэлектрика Е=Е0-Е1.
|
14.
Мы уже говорили, что диэлектрики бывают полярные и неполярные. Если во внешнее электрическое поле Е попадает диэлектрик с неполярными молекулами, то в молекулах происходит смещение зарядов и образуются диполи. Такая поляризация называется деформационной. В этом случае возникающий вследствие смещения зарядов средний электрический момент молекулы т пропорционален напряженности внешнего поля Е, т. е.
т = (17-1)
где коэффициент а называется поляризуемостью молекулы.
В том случае, когда диэлектрик состоит из полярных молекул, каждая молекула является диполем. В результате хаотического теплового движения молекул средний электрический момент во всех направлениях равен нулю. Но при наложении на полярный диэлектрик внешнего электрического поля с напряженностью Е
"Курчатов Игорь Васильевич (1903—1960) — советский физик, академик. Создал новые области науки — сегнетоэлектриче- ство, ядерную изомерию; много нового дал в области ядерных реакций. Обеспечил СССР ведущее положение в ядерной физике. Герой Социалистического Труда.
** В у л Бенцион Моисеев-ич (род в 1903 г.) — советский исследователь диэлектриков. Лауреат Государственной премии v-LCP 1946 г.
возникает ориентационная поляризация диэлектрика, при которой средний электрический момент молекулы т уже не равен нулю.
Из закона распределения Больцмана (см. т.1, стр. 252), выводится зависимость среднего электрического момента молекулы т при ориентационной поляризации от абсолютного электрического момента молекулы М, напряженности внешнего поля Е и абсолютной температуры Т:
Я. (17-2)
Здесь постоянная Больцмана £=1,38- 10-1е эрг • град-1. Как видно из формулы, с повышением температуры средний электрический момент молекулы уменьшается.
В неполярных диэлектриках имеет место деформационная поляризация, обусловленная смещением электронов. В полярных диэлектриках возникает ориентационная поляризация, но возможна также и деформационная, вызванная смещением зарядов (ионная поляризация). В этом случае средний электрический момент молекулы диэлектрика, находящейся во внешнем поле Е, выражается суммой:
<17-з>
Введем коэффициент
Р = (17-4)
Вспомним, что между индукцией D, напряженностью Е и вектором поляризации Р существует соотношение
D = Е + 4кР = s£. (17-5)
Введем число молекул в единице объема п. Тогда
Р = пт.
Доказано, что т = -f -i npj . (17-6)
Но
Р = 1).
Значит,
>
Итак,
= Я(в—1). (17-7)
Отсюда получается формула для диэлектрической проницаемости:
1=1 (17-8)
£ +2 3
Можно перейти от единицы объема к молю вещества диэлектрика. Обозначив р — плотность, р. — молекулярный вес диэлектрика, N — число Авогадро, имеем
No
п = —.
вид:
Поэтому формула для диэлектрической проницаемости примет
Iii = ±*Wp. (17-9)
£ +2 Р 3
Правую часть этого уравнения называют молярной поляризацией. Она состоит из двух частей:
а) Поляризация смещения или деформационная, обусловленная появлением новых моментов в неполярных молекулах:
— = (17-10)
е +2 Р 3 '
В этом виде формула была выведена Мосотти в 1850 г. и Клаузиусом* в 1870 г. и получила название уравнения Мосотти — Клаузиуса.
б) Ориентационная поляризация полярных молекул
е — 1 fx AkNM*
е +2 Р 9kT Эту формулу, а равно и общую формулу
(17-11)
LzIJL^UNU + J*) (17-12)
S +2 Р 3 \ 1 ЪкТ} v '
вывел в 1912 г. П. И. Д е б а й**.
Иногда вещества с полярными молекулами называют параэлек- трическими, тогда слово диэлектрические относится лишь к веществам с неполярными молекулами. К диэлектрикам относятся: воздух, окись углерода, пары брома, жидкий кислород; к параэлект- рикам: аммиак, бензол, лед, вода, глицерин, спирт.
♦Рудольф Клаузиус (1822—1888), немецкий физик. Выдающиеся работы по термодинамике, кинетической теории, по электричеству.
#* Петер Иозеф Дебай (род. в 1884 г.) — голландец, с 1940 р. в США. Лауреат Нобелевской премии 1936 г. по химии за его вклады в знание структуры молекул путем исследований дипольных моментов и дифракции рентгеновых лучей и электронов в газах.
Зн. В. Кашин
65
Если обозначить молярную поляризацию буквой Р, то
P==LldJi. (17-13)
Е +2 Р
Формулу Д е б а я можно сокращенно записать?
Р = а + (17-14)
Пользуясь этой формулой, можно экспериментально определить абсолютные дипольные моменты молекул данного вещества М. Для этого на диаграмму наносят величину молярной поляризации Р в зависимости от 1/7". Получаются прямые линии, по которым можно определить М. Дипольные моменты молекул оказались в системе СГСЭ порядка 10~18, что и следовало ожидать, так как элементарный заряд в системе СГСЭ равен 4,8 • 10~10, а размер молекул порядка 10~8см. Одноатомные молекулы (например, гелия, неона, аргона) неполярны. Двухатомные молекулы из двух одинаковых атомов (кислорода, азота) тоже неполярны. Но если атомы в молекуле сильно разнятся (например, в соляной кислоте, воде), то М получается очень большим. Если же эти атомы близки в периодической системе (например, окись углерода), М мало. В сложных молекулах общий дипольный момент приближенно равен геометрической сумме моментов отдельных полярных групп.
На рис. 46 изображена зависимость молекулярной поляризуемости Р = от обратной величины абсолютной температуры 1/7\ Как видим, диэлектрическая проницаемость при деформационной поляризации 1 не зависит от температуры и является величиной, обратно пропорциональной плотности. В случае ориентационной поляризации 2 молекулярная поляризация обратно пропорциональна температуре. При наличии обоих видов поляризации линия 3 изображает изменение Р в зависимости от ИТ.
Полярностью молекул объясняется способность их абсорбироваться на поверхностях раздела фаз.
15.
Диэлектрик, помещенный во внешнее электрическое поле, поляризуется под действием этого поля. Поляризацией диэлектрика называется процесс приобретения им отличного от нуля макроскопического дипольного момента. Степень поляризации диэлектрика характеризуется векторной величиной, которая называется поляризованостью или вектором поляризации (P). Поляризованность определяется как электрический момент единицы объема диэлектрика
![]() ,
,
где
N
- число молекул в объеме
![]() .
Поляризованность P
часто называют поляризацией, понимая
под этим количественную меру этого
процесса.
В диэлектриках различают
следующие типы поляризации: электронную,
ориентационную и решеточную (для ионных
кристаллов).
Электронный
тип поляризации
характерен для диэлектриков с неполярными
молекулами. Во внешнем электрическом
поле (рис. 2.1) положительные заряды внутри
молекулы смещаются по направлению поля,
а отрицательные в противоположном
направлении, в результате чего молекулы
приобретают дипольный момент, направленный
вдоль внешнего поля
.
Поляризованность P
часто называют поляризацией, понимая
под этим количественную меру этого
процесса.
В диэлектриках различают
следующие типы поляризации: электронную,
ориентационную и решеточную (для ионных
кристаллов).
Электронный
тип поляризации
характерен для диэлектриков с неполярными
молекулами. Во внешнем электрическом
поле (рис. 2.1) положительные заряды внутри
молекулы смещаются по направлению поля,
а отрицательные в противоположном
направлении, в результате чего молекулы
приобретают дипольный момент, направленный
вдоль внешнего поля

Индуцированный
дипольный момент молекулы пропорционален
напряженности внешнего электрического
поля
![]() ,
где
,
где
![]() -
поляризуемость молекулы. Значение
поляризованности в этом случае равно
-
поляризуемость молекулы. Значение
поляризованности в этом случае равно
![]() ,
где n
- концентрация молекул
,
где n
- концентрация молекул
![]() ;
;
![]() -
индуцированный дипольный момент
молекулы, который одинаков для всех
молекул и направление которого совпадает
с направлением внешнего поля.
Ориентационнный
тип поляризации
характерен для полярных диэлектриков.
В отсутствие внешнего электрического
поля молекулярные диполи ориентированы
случайным образом, так что макроскопический
электрический момент диэлектрика равен
нулю.
-
индуцированный дипольный момент
молекулы, который одинаков для всех
молекул и направление которого совпадает
с направлением внешнего поля.
Ориентационнный
тип поляризации
характерен для полярных диэлектриков.
В отсутствие внешнего электрического
поля молекулярные диполи ориентированы
случайным образом, так что макроскопический
электрический момент диэлектрика равен
нулю.
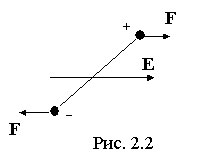
Если
поместить такой диэлектрик во внешнее
электрическое поле, то на молекулу-диполь
будет действовать момент сил (рис. 2.2),
стремящийся ориентировать ее дипольный
момент в направлении напряженности
поля. Однако полной ориентации не
происходит, поскольку тепловое движение
стремится разрушить действие внешнего
электрического поля.
Такая
поляризация называется ориентационной.
Поляризованность в этом случае равна
![]() ,
где <p>
- среднее значение составляющей дипольного
момента молекулы в направлении внешнего
поля.
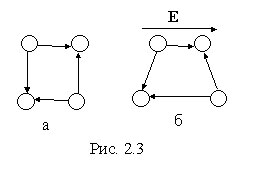
Решеточный
тип поляризации
характерен для ионных кристаллов. В
ионных кристаллах (NaCl и т.д.) в отсутствие
внешнего поля дипольный момент каждой
элементарной ячейки равен нулю (рис.
2.3.а), под влиянием внешнего электрического
поля положительные и отрицательные
ионы смещаются в противоположные стороны
(рис. 2.3.б). Каждая ячейка кристалла
становится диполем, кристалл поляризуется.
Такая поляризация называется решеточной.
Поляризованность и в этом случае можно
определить как
,
где <p>
- среднее значение составляющей дипольного
момента молекулы в направлении внешнего
поля.
Решеточный
тип поляризации
характерен для ионных кристаллов. В
ионных кристаллах (NaCl и т.д.) в отсутствие
внешнего поля дипольный момент каждой
элементарной ячейки равен нулю (рис.
2.3.а), под влиянием внешнего электрического
поля положительные и отрицательные
ионы смещаются в противоположные стороны
(рис. 2.3.б). Каждая ячейка кристалла
становится диполем, кристалл поляризуется.
Такая поляризация называется решеточной.
Поляризованность и в этом случае можно
определить как
![]() ,
где
-
значение дипольного момента элементарной
ячейки, n
- число ячеек в единице объема.
,
где
-
значение дипольного момента элементарной
ячейки, n
- число ячеек в единице объема.
Поляризованность
изотропных диэлектриков любого типа
связана с напряженностью поля соотношением
![]() ,
где
,
где
![]() -
диэлектрическая
восприимчивость
диэлектрика.
-
диэлектрическая
восприимчивость
диэлектрика.

15-16.
|
|
|
|
|
17.
|
Вектор электрического смещения |
|
|
|
Имеем
границу раздела двух сред с
а б Рис. 4.10 Как мы уже показали, в соответствии с (4.1.10),
т.е., напряженность электростатического поля E изменяется скачком при переходе из одной среды в другую. Главная
задача электростатики – расчет
электрических полей, то есть
Для упрощения расчетов была введена новая векторная величина – вектор электрического смещения (электрическая индукция):
Из
предыдущих рассуждений
Таким
образом, вектор
где
Таким
образом, вектор
–
есть сумма (линейная комбинация) двух
векторов различной природы:
–
главной характеристики поля и
В
СГС:
В
СИ:
Для
точечного заряда в вакууме
Для имеет место принцип суперпозиции, как и для , т.е.
|
18.
Диэлектрическая проницаемость вещества |
|
|
Автор Administrator |
18:01:2012 г. |
Диэлектрическая проницаемость вещества–отношение модулей напряженности - силы поля в ваккуме и в веществе. Она больше у полярных веществ, способных поляризоваться, обращающих противоположные заряды к полю. Это связано с полярностью связей и электроотрицательностью их элементов. У воды благодаря полярным связям Н-О высокая д.п.-ε=81.Взаимодействие между зарядами по закону Кулону F =-kq1q2/r2=Eq,как и напряженность Е=εЕo,поэтому также ослабляется вεраз и вычисляется по формуле F=-kq1q2/εr2или F=q1q2/4πεoεr2,φ=q/4πεoεr (напомним, что коэффициент пропорциональности в вакууме k=9.109Н.м2/Кл2,записывается и какk=1/4πεo,гдеεo=8.85.10-12Кл2/Н.м2 –электрическая постоянная или диэлектрическая проницаемость вакуума, связанная со скоростью света Максвеллом). При графическом изображении силовые линии поля внутри диэлектрика в ε раз реже, чем вне, в вакууме или воздухе (ε воздуха близка 1, как у вакуума) Диэлектрики по полярности и диэлектрической проницаемости разделяют на неполярные (симметричные молекулы, где центры зарядов совпадают – неметаллов, метана, бензола) и полярные (как вода, спирт и другие, их молекулы можно расматривать как диполи, с зарядами–q +q на расстоянии d).А также сегнетоэлектрики – вещества с очень большой диэлектрической проницаемостью, подобные сегнетовой соли (сε=100 000, как кристаллы титаната бария BaTiO3, LiNbO3, KH2PO4). Проводники и электрические системы могут изменять и накапливать заряды. Это свойство названо электроемкостью (В 18 веке ее представляли как емкость для сохранения электрической жидкости от испарения). Опыт показывает, что увеличение электрического заряда приводит к увеличению напряжения, отношение заряда к напряжению сохраняется и может характеризовать емкость, способность накапливать заряды С=q/U. |
19.
Теорема Гаусса для электрического поля в диэлектриках (интегральная и дифференциальная формы). Граничные условия на границе раздела двух диэлектриков.
Влияние
диэлектрика на электрическое поле
сводится к действию поляризационных
зарядов. Поэтому к диэлектрикам можно
применить соотношение
![]() ,
добавив при этом к свободным зарядам
q поляризационные заряды qпол,
и подставив qпол из формулы
для объемных поляризационных зарядов,
ограниченных замкнутой поверхностью
S:
,
добавив при этом к свободным зарядам
q поляризационные заряды qпол,
и подставив qпол из формулы
для объемных поляризационных зарядов,
ограниченных замкнутой поверхностью
S:
![]() .
Получим:
.
Получим:![]() .
Введя новый вектор, называемый вектор
электрического смещения
.
Введя новый вектор, называемый вектор
электрического смещения![]() (1),
имеем теорему Гаусса для электрического
поля в диэлектрике
(1),
имеем теорему Гаусса для электрического
поля в диэлектрике![]() ,
или
,
или![]() (2)
. Подставляя (1) в (2), и имея аналогичное
равенство
(2)
. Подставляя (1) в (2), и имея аналогичное
равенство![]() ,
получаем
,
получаем
![]()
Граничные условия
Пусть
есть заряженная поверхность с плотностью
зарядов σ. Возьмем бесконечно малый
цилиндр, с основаниями по разные стороны
заряженной поверхности. Высота цилиндра
пусть будет бесконечно малой по сравнению
с его площадью ΔS. Внутри цилиндра
находится заряд σΔS.
Сумма потоков
вектора![]() через
основания будет
через
основания будет
![]() ,
поток через
боковую поверхность пренебрежимо мал.
По теореме Гаусса, это равно
4πσΔS. Отсюда
,
поток через
боковую поверхность пренебрежимо мал.
По теореме Гаусса, это равно
4πσΔS. Отсюда
![]() .
Видим, если на границе нет свободных
зарядов, то D1n=D2n
.
.
Видим, если на границе нет свободных
зарядов, то D1n=D2n
.
Для
вектора![]() остаются
непрерывными тангенциальные составляющие.
Доказательство: можно представить, что
полное поле в любой точке складывается
из поля, создаваемого зарядами самой
площадки Евнутр,
и поля, создаваемого всеми остальными
зарядами Евнеш.
Сама же площадка на близких расстояниях
ведет себя как бесконечная заряженная
плоскость. Создаваемое ею поле Евнутр
нормально к площадке и равно 2πσ.
Но направления этого поля по разные
стороны противоположны, и дают в сумме
4πσ.
Значит, скачок претерпевает только
внутреннее поле, а внешнее меняется
непрерывно. А так как внутреннее поле
не имеет тангенциальной составляющей,
то тангенциальная составляющая полного
поля меняется также непрерывно: E1t=E2t
.
остаются
непрерывными тангенциальные составляющие.
Доказательство: можно представить, что
полное поле в любой точке складывается
из поля, создаваемого зарядами самой
площадки Евнутр,
и поля, создаваемого всеми остальными
зарядами Евнеш.
Сама же площадка на близких расстояниях
ведет себя как бесконечная заряженная
плоскость. Создаваемое ею поле Евнутр
нормально к площадке и равно 2πσ.
Но направления этого поля по разные
стороны противоположны, и дают в сумме
4πσ.
Значит, скачок претерпевает только
внутреннее поле, а внешнее меняется
непрерывно. А так как внутреннее поле
не имеет тангенциальной составляющей,
то тангенциальная составляющая полного
поля меняется также непрерывно: E1t=E2t
.
20.