Инвариантность формы дифференциала

Рассмотрим сложную функцию y=f(u(x)). Пусть функции y=f(u), u=u(x) дифференцируемы, тогда 

Таким образом, если аргументом функции является функция другого аргумента, то форма дифференциала совпадает с формой дифференциала (7), когда аргументом функции является независимая переменная. Это свойство называется инвариантностью формы дифференциала.

Билет 43

Если у есть неявная функция от х, т.е. задана уравнением F(x,y)=0, не разрешенным относительно у, то для нахождения производной нужно продифференцировать по х обе части равенства, помня, что у есть функция от х, и затем разрешить полученное равенство относительно у'.

Пример. Найти производную неявной функции х²+у²-4х-10у+4=0.

Дифференцируя по х, получаем 2х+2у *у' -4-10у'=0. Выражаем у', имеем:

Функция задана параметрически, если зависимость функции y от аргумента x задана посредством параметра t:

  

Производная параметрической функции равна частному производных y и x, взятых по переменной t:

  

или в других обозначениях

  

Билет 42

Производная произведения функций.

Пусть u(x) и u(x) - дифференцируемые функции. Тогда произведение функций u(x)v(x) также дифференцируемо и

Внимание:  Производная произведения двух функций НЕ РАВНА произведению производных этих функций!

Производная частного функций.

Пусть u(x) и u(x) - дифференцируемые функции. Тогда, если v(x) ≠ 0, то производная частного этих функций вычисляется по формуле

"Двухслойная" сложная функция записывается в виде

где u = g(x) - внутренняя функция, являющаяся, в свою очередь, аргументом для внешней функции f.  Если f и g - дифференцируемые функции, то сложная функция   также дифференцируема по x и ее производная равна

Данная формула показывает, что производная сложной функции равна произведению производной внешней функции на производную от внутренней функции. Важно, однако, что производная внутренней функции вычисляется в точке x, а производная внешней функции - в точке u = g(x)!  Эта формула легко обобщается на случай, когда сложная функция состоит из нескольких "слоев", вложенных иерархически друг в друга. 

Понятие логарифмической производной

 

Логарифмической производной положительной функции   называется производная  . Так как  , то по правилу дифференцирования сложной функции получим следующее соотношение для логарифмической производной:

.  

С помощью логарифмической производной удобно вычислять обычную производную в тех случаях, когда логарифмирование упрощает вид функции.

Билет 41)

Пусть функция f(x) определена на промежутке (a; b),   и   - точки этого промежутка.Производной функции f(x) в точке   называется предел отношения приращения функции к приращению аргумента при  . Обозначается  .

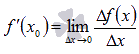Если функция f(x) дифференцируема в каждой точке некоторого промежутка (a; b), то функцию называют дифференцируемой на этом промежутке. Таким образом, любой точке x из промежутка (a; b) можно поставить в соответствие значение производной функции в этой точке  , то есть, мы имеем возможность определить новую функцию  , которую называют производной функции f(x) на интервале (a; b).