Структура алу для умножения чисел с фиксированной точкой.
Так как операция умножения относится к длинным операциям, для уменьшения времени ее выполнения существуют различные методы ускорения. Все методы делят на аппаратные и логические. И те и другие методы требуют дополнительных затрат оборудования. При использовании аппаратных методов дополнительные затраты оборудования прямопропорциональны числу разрядов. Данные методы вызывают усложнение схемы, ее удорожание и снижение надежности. Логические методы не зависят от разрядов операндов. Усложняется схема управления АЛУ(Алгоритм работы).Обычно применяется комбинация данных методов.
К аппаратным методам относятся:
1)выполнение операции сложения и сдвига позволяющие за 1 такт производить сдвиг информации сразу на несколько разрядов.
2)совмещение операций сложения и сдвига.
3)построение комбинационных схем множительных устройств (реализация табличного умножения).
Среди логических методов наиболее распространены методы позволяющие за один цикл умножения обработать сразу несколько разрядов множителя.
Структурная схема АЛУ для ускоренного умножения чисел в формате с фиксируемой запятой.
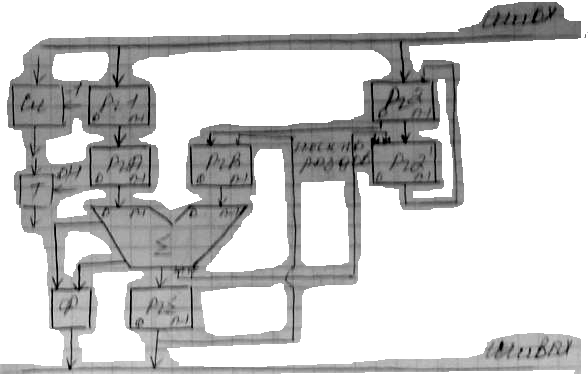
АЛУ вкл.
- Входной регистр множимого Рг1, -Регистры множителя Рг2 и Рг2’, -Сумматор для образования суммы частичных произведений,- РгА -для формирования частичного произведения ,-РгВ -для накопления суммы частичных произведений, -Рг См -регистр суммы, -Сч- счетчик циклов, - Т-тригер коррекции
Последовательность выполнения операции состоит из следующих частей:
1. Начальная установка.
2. Вычисление суммы частичных произведений.
3. Вывод результата.
Методы ускорения умножения.
Методы ускорения умножения делятся на аппаратурные и логические. Как те, так и другие требуют дополнительных затрат оборудования. При использовании аппаратурных методов дополнительные затраты оборудования прямо пропорциональны числу разрядов в операндах. Эти методы вызывают усложнение схемы АЛУ.
Дополнительные затраты оборудования при реализации логических методов ускорения умножения не зависят от разрядности операндов. Усложняется в основном схема АЛУ. В ЭВМ для ускорения умножения часто используется комбинации этих методов.
К аппаратурным методам ускорения умножения относятся ускорение выполнения операций сложения и сдвига, введение дополнительных цепей сдвига, позволяющих за один такт производить сдвиг информации в регистрах сразу на несколько разрядов, совмещение по времени операций сложения и сдвига, построение комбинационных схем множительных устройств, реализующих «табличное» умножение.
Среди логических методов наиболее распространены в настоящее время методы, позволяющие за один шаг умножения обработать несколько разрядов множителя.
Структура алу для деления чисел с фиксированной точкой.
При делении чисел с фиксированной запятой сама операция сводится к операциям вычитания (сложения) и сдвига.
Деление реализуется двумя основными способами:
Деление с неподвижным делимым и сдвигаемым вправо делителем.
Деление с неподвижным делителем и сдвигаемым вправо делимым.
Деление с неподвижным делителем с восстановлением остатка.
Алгоритм деления аналогичен алгоритму деления уголком, используемом при ручном счете.
Z=X/Y
X – делимое. Обычно представляется двойным словом (содержит 2n или 2n-1 разрядов), Y – делитель,
Z – частное (содержит n или n-1 разряд).
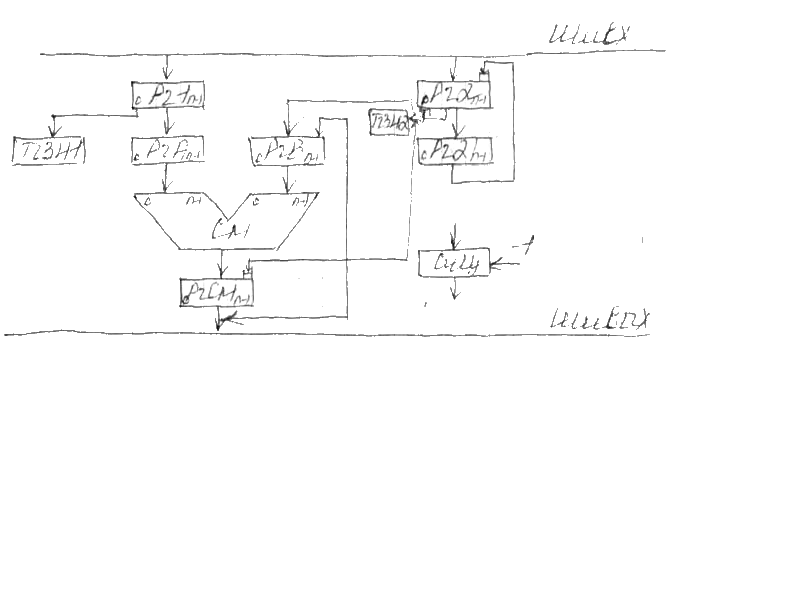
Данная схема имеет 2 разновидности:
Деление с неподвижным делителем с восстановлением остатка.
Деление с неподвижным делителем без восстановления остатка.
1.1) Берутся модули от делимого и делителя. СчЦ (счетчик цикла) устанавливается в значение разрядности регистров.
1.2) Исходное значение частичного остатка делится равным старшим разрядам делимого двойной длины. Младшая и старшая часть делимого хранится в разных регистрах одинаковой длины.
1.3) Частичный остаток удваивается путем сдвига на 1 разряд влево. При этом в освободившийся при сдвиге младший разряд частичного остатка заносится очередная цифра делимого из разрядов младшей половины делимого (регистр 2 нулевой разряд).
1.4) Из сдвинутого частичного остатка вычитается делитель и анализируется знак результата вычитания. Если результат вычитания положителен, то очередная цифра частного равна 1, если результат вычитания отрицателен, то очередная цифра равна 0.
Данные этапы выполняются последовательно для получения всех цифр модуля частного.
1.5) Происходит вычисление знака частного (XOR).
Существует другой метод деления – деление без восстановления остатка.
Данные два способа отличаются последовательностью вычисления частного и остатка. В первом методе сначала вычислялось частное, потом вычислялся остаток, во втором методе одновременно вычислялся (на каждом цикле) и частное, и остаток.
Этапы алгоритма деления без восстановления остатка:
1) Берутся модули от делимого и делителя, в СчЦ (счетчик цикла) устанавливается значение разрядности регистров.
2) Исходное значение частичного остатка делается равным старшим разрядам делимого двойной длины. Младшая и старшая часть делимого содержатся в разных регистрах одинаковой длины.
3) Частичный остаток удваивается путем сдвига на 1 разряд влево. При этом в освобождающийся при сдвиге младший разряд заносится очередная цифра делимого.
4) Если остаток больше нуля, то из сдвинутого частичного остатка вычитается делитель; если остаток меньше нуля, то к сдвинутому частичному остатку прибавляется делитель.
5) Если результат вычитания больше нуля, то очередная цифра модуля частного равна 1; если результат вычитания меньше нуля, то очередная цифра модуля частного равна 0. Данные этапы выполняются до получения всех цифр модуля частного.
6) Определяется знак частного (XOR)
1. АЛУ для выполнения различных арифметических действий структурно почти идентичны, что позволяет реализовать как блочные, так и многофункциональные АЛУ.
2. Ускорение вычислений может достигаться алгоритмически (появление новых связей, изменение алгоритма работы) либо улучшением элементной базы (внедрение 2n, 4n разрядных устройств).