
- •Фоннеймановская архитектура вм.
- •Алгоритм выборки команды в вм с фоннеймановской архитектурой.
- •Представление чисел в вм.
- •Сумматоры.
- •Арифметико-логические устройства. Их классификация.
- •Структура алу для умножения чисел с фиксированной точкой.
- •Методы ускорения умножения.
- •Структура алу для деления чисел с фиксированной точкой.
- •Операции десятичной арифметики.
- •Операции над числами с плавающей точкой.
- •Многофункциональные алу.
- •Устройство управления с жесткой логикой.
- •Принцип микропрограммного управления.
- •Память эвм. Назначение. Классификация. Основные
- •Иерархия памяти эвм и вс.
- •Адресные и безадресные зу.
- •Классификация вычислительных систем.
- •Структуры многопроцессорных систем с распределенной памятью.
- •Многопроцессорные системы с общей памятью.
- •Распараллеливание вычислительных процессов.
- •Параллелизм на уровне выполнения команд.
- •Ускорение работы процессора. Конвейерная организация.
- •Конфликты, возникающие при конвейерной организации.
- •Проблемы, возникающие при выполнении команд перехода на конвейере.
- •Типы архитектур процессоров.
- •Скалярные и векторные процессоры.
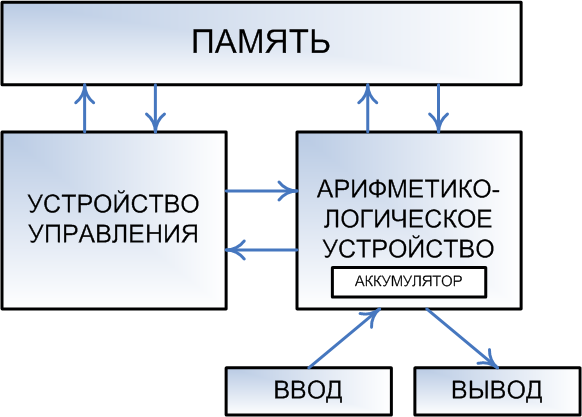
Фоннеймановская архитектура вм.
П
 ринцип
двоичного кодирования.
ринцип
двоичного кодирования.
Принцип однородности памяти.
Как программы (команды), так и относящиеся к программам данные хранятся в одной и той же памяти
Принцип адресуемости памяти.
Структурно основная память состоит из пронумерованных ячеек;
Все команды располагаются в памяти и выполняются последовательно, одна после завершения другой, в последовательности, определяемой программой.
Принцип жесткости архитектуры.
Неизменяемость в процессе работы топологии, архитектуры, списка команд.
Компьютеры, построенные на этих принципах, относят к типу фоннеймановских.
Алгоритм выборки команды в вм с фоннеймановской архитектурой.
К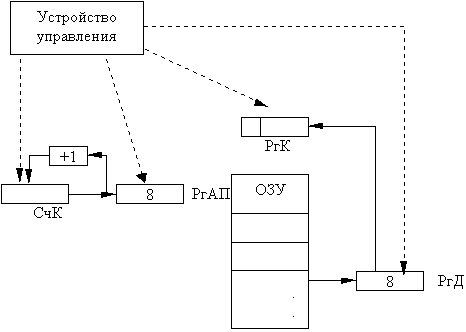 огда
устройство управления завершит выполнение
команды, оно должно выбрать следующую
команду из памяти в РгК. Адрес следующей
команды содержится в специальном
регистре, называемом Счетчиком Команд
(СчК). Всякий раз при выборке команды
устройство управления одновременно
увеличивает содержимое СчК на единицу,
чтобы после выполнения команды можно
было произвести выборку следующей.
Таким образом, устройство управления
работает с командами в порядке, в котором
они помещены в ОЗУ.
огда
устройство управления завершит выполнение
команды, оно должно выбрать следующую
команду из памяти в РгК. Адрес следующей
команды содержится в специальном
регистре, называемом Счетчиком Команд
(СчК). Всякий раз при выборке команды
устройство управления одновременно
увеличивает содержимое СчК на единицу,
чтобы после выполнения команды можно
было произвести выборку следующей.
Таким образом, устройство управления
работает с командами в порядке, в котором
они помещены в ОЗУ.
Последовательность выборки команды:
а) копируется адрес следующей команды из СчК в РгАП (адрес 8 в примере на рис);
б) прибавляется 1 к содержимому СчК СчК:=СчК+1 ( 9 );
в) содержимое ячейки (команда), которая адресуется РгАП, пересылается в РгД;
г) содержимое РгД копируется в РгК.
*РгАП – регистр адреса памяти
Представление чисел в вм.
Машинным изображением числа называют его представление в разрядной сетке ЭВМ. В вычислительных машинах применяются две формы представления чисел:
естественная форма или форма с фиксированной запятой (точкой);
нормальная форма или форма с плавающей запятой (точкой);
Пример: (естественная форма) 452,34 = 452340*10-3 = 0,0045234*105 = 0,45234*103(нормальная форма)
Всякое десятичное число, прежде чем оно попадает в память компьютера, преобразуется по схеме: X10 → X2 = M1 × [102]r
После этого осуществляется ещё одна важная процедура: мантисса с её знаком заменяется кодом мантиссы с её знаком; порядок числа с его знаком заменяется кодом порядка с его знаком.
Существуют следующие коды двоичных чисел:
Прямой код; Обратный код; Дополнительный код.
Последние две формы применяются особенно широко, так как позволяют упростить конструкцию арифметико-логического устройства компьютера путем замены разнообразных арифметических операций операцией сложения.
Сумматоры.
А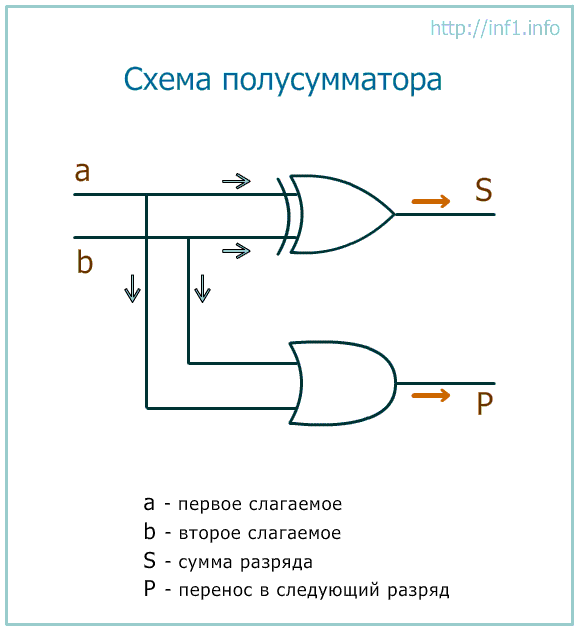 рифметико-логическое
устройство процессора (АЛУ) обязательно
содержит в своем составе такие элементы
как сумматоры. Эти схемы позволяют
складывать двоичные числа.
рифметико-логическое
устройство процессора (АЛУ) обязательно
содержит в своем составе такие элементы
как сумматоры. Эти схемы позволяют
складывать двоичные числа.
Как происходит сложение? Допустим, требуется сложить двоичные числа 1001 и 0011. Сначала складываем младшие разряды (последние цифры): 1+1=10. Т.е. в младшем разряде будет 0, а единица – это перенос в старший разряд. Далее: 0 + 1 + 1(от переноса) = 10, т.е. в данном разряде снова запишется 0, а единица уйдет в старший разряд. На третьем шаге: 0 + 0 + 1(от переноса) = 1. В итоге сумма равна 1100.
Сумматор учитывает перенос из предыдущего разряда, поэтому имеет три входа.
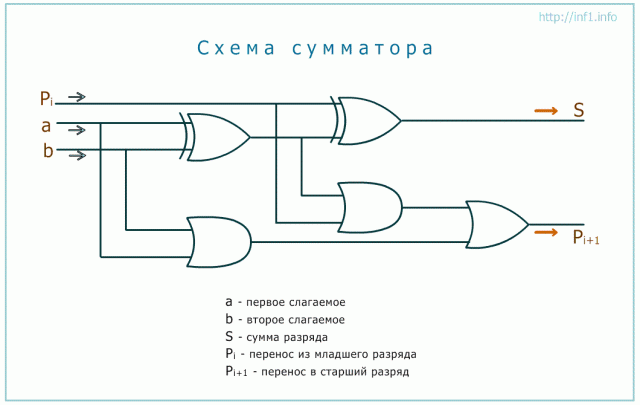 Чтобы
учесть перенос приходится схему
усложнять. По-сути она получается,
состоящей из двух полусумматоров.
Чтобы
учесть перенос приходится схему
усложнять. По-сути она получается,
состоящей из двух полусумматоров.
Р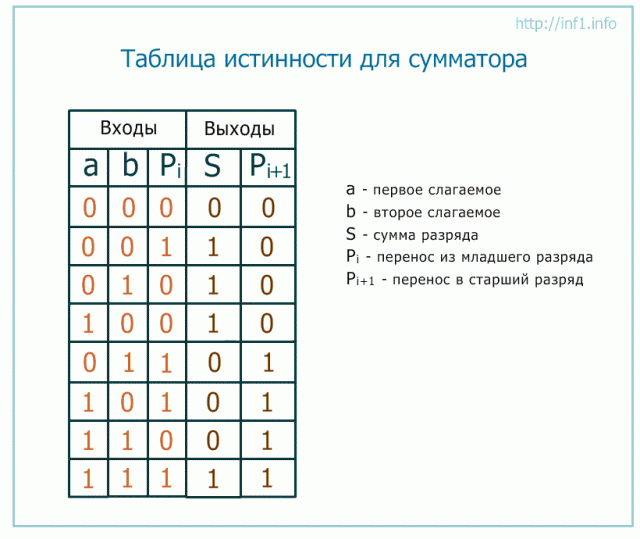 ассмотрим
один из случаев. Требуется сложить 0 и
1, а также 1 из переноса. Сначала определяем
сумму текущего разряда. Судя по левой
схеме ИСКЛЮЧАЮЩЕЕ ИЛИ, куда входят a и
b, на выходе получаем единицу. В следующее
ИСКЛЮЧАЮЩЕЕ ИЛИ уже входят две единицы.
Следовательно, сумма будет равна 0.
ассмотрим
один из случаев. Требуется сложить 0 и
1, а также 1 из переноса. Сначала определяем
сумму текущего разряда. Судя по левой
схеме ИСКЛЮЧАЮЩЕЕ ИЛИ, куда входят a и
b, на выходе получаем единицу. В следующее
ИСКЛЮЧАЮЩЕЕ ИЛИ уже входят две единицы.
Следовательно, сумма будет равна 0.
Теперь смотрим, что происходит с переносом. В один вентиль И входят 0 и 1 (a и b). Получаем 0. Во второй вентиль (правее) заходят две единицы, что дает 1. Проход через вентиль ИЛИ нуля от первого И и единицы от второго И дает нам 1.
Проверим работу схемы простым сложением 0 + 1 + 1 = 10. Т.е. 0 остается в текущем разряде, и единица переходит в старший. Следовательно, логическая схема работает верно.
Работу данной схемы при всех возможных входных значениях можно описать следующей таблицей истинности.
