6. Способы задания плоскости на чертеже. Главные линии плоскости

   Множество элементов плоскости изобразить на чертеже нельзя. Поэтому плоскость принято изображать геометрическими элементами, лежащими в плоскости.     Задание плоскости тремя точками. Три точки, не лежащие на одной прямой, задают плоскость (рис.3.6а).

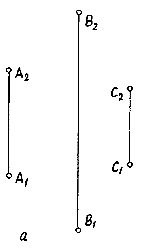 Рис. 3.6-a 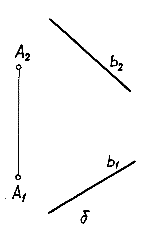  Рис. 3.6-б

   Задание плоскости прямой и точкой вне этой прямой. Если две точки плоскости соединить прямой, то получим задание плоскости прямой и точкой (рис.3.6-б). Всякий дополнительный элемент (точка, прямая), взятый произвольно, как правило, не будет принадлежать этой плоскости. Определитель: (A, b)[Ab]. 

   Задание плоскости двумя пересекающимися прямыми. Две пересекающиеся прямые определяют плоскость (рис.3.6-в). Определитель: (A, b)[Ab]. 

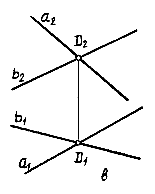    В ряде случаев плоскость удобно задавать двумя пересекающимися прямыми уровня: горизонталью и фронталью (рис.3.6-г).

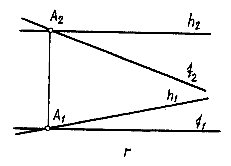  Рис. 3.6-в  Рис. 3.6-г

   

Задание плоскости двумя параллельными прямыми. Так как параллельные прямые можно рассматривать как пересекающиеся в несобственной точке, то они также будут определять плоскость (рис.3.6-д). Определитель: (ab).     Задание плоскости плоской фигурой (отсек плоскости). Любая плоская фигура, например треугольник, задает плоскость (рис.3.6-е). Плоская фигура придает большую наглядность изображаемой плоскости. Определитель: (ABC).

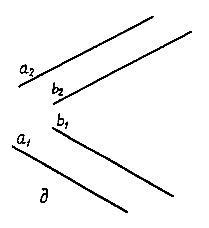 Рис. 3.6-д 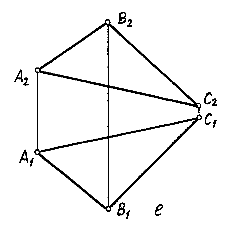  Рис. 3.6-е

   Необходимо отметить, что при всех случаях задания плоскость считается бесконечной. 

Главные линии плоскости это линии уровня (горизонталь и фронталь) и линия наибольшего наклона (линия ската).Фронтали – прямые линии, лежащие в плоскости и параллельные фронтальной плоскости проекций. Горизонтали - прямые линии, лежащие в плоскости и параллельные горизонтальной плоскости проекций. Линии наибольшего наклона (ската) – прямые линии, лежащие в плоскости и перпендикулярные горизонтали этой плоскости.

7 Вопрос Плоскость общего положения и ее проекции

Плоскость общего положения.Плоскость а, наклонная ко всем плоскостям проекций, называется плоскостью общего положения (фиг.223,а).

Особенностью этой плоскости является то, что всякая кривая и фигура, лежащие в этой плоскости, при проектировании не имеют ни одной проекции, равной натуральной (истинной) величине. Все ее следы k, L и m наклонены к осям х, z и у, замыкаясь, образуют фигуру треугольника, называемого треугольником следов. Такую плоскость можно изображать проекциями ее следов.

8.Плоскости частного положения. Особенности их проекций

 Плоскость, перпендикулярная одной плоскости проекций. Такие плоскости получили название проецирующих плоскостей. Горизонтально проецирующей плоскостью называют плоскость, перпендикулярную к плоскости проекций П₁ (рис.3.7). 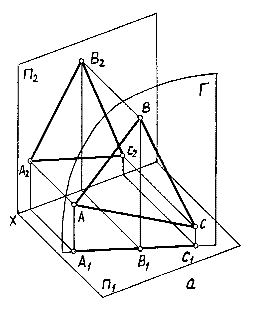  Рис. 3.7-а   Рис. 3.7-б

     Любой элемент, лежащий в этой плоскости, проецируется на плоскость П₁ в прямую Г₁, называемую горизонтальным следом плоскости. Угол наклона  горизонтально проецирующей плоскости к плоскости проекций П₂ на комплексном чертеже определяется как угол ₁, заключенный между горизонтальным следом Г₁ данной плоскости и прямой, перпендикулярной линиям связи (рис.3.7-б).   Рис. 3.8-а   Рис. 3.8-б

 

  

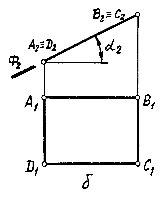
Ф ронтально проецирующей плоскостью (рис.3.8) называют плоскость, перпендикулярную к плоскости проекций П₂. Любой элемент этой плоскости проецируется на фронтальную плоскость проекций в прямую Ф₂ - фронтальный след плоскости. Угол наклона  фронтально проецирующей плоскости к плоскости П₁ на комплексном чертеже определяется как угол ₂, заключенный между фронтальным следом Ф₂ и прямой, перпендикулярной линиям связи.      Профильно проецирующей плоскостью называют плоскость, перпендикулярную к профильной плоскости проекций (рис.3.9). Любой элемент, лежащий в этой плоскости, проецируется на профильную плоскость проекций в прямую ₃ - профильный след плоскости. На профильной проекции углы  и  наклона профильно проецирующей плоскости к плоскостям П₂ и П₂изображаются без искажения.   Рис. 3.9.

Плоскости частного положения, перпендикулярные двум плоскостям проекций и параллельные третьей плоскости проекций, называются плоскостями уровня: фронтальная плоскость уровня параллельна плоскости проекций V и перпендикулярна плоскостям Н и W.Её признаки: её горизонтальная и профильная проекции представляют собой прямые, параллельные осям Х и Z. Горизонтальная плоскость уровня параллельна плоскости проекций Н и перпендикулярна плоскостям V и W; Признаки: ее фронтальная и профильная проекции проецируются в прямые, параллельные осям Х и У. Профильная плоскость уровня параллельна плоскости проекций W и перпендикулярна плоскостям V и Н; Признаки: ее фронтальная и горизонтальная проекции представляют собой прямые, перпендикулярные оси Х.