Умножение матрицы на число
Умножение матрицы A на число λ (обозначение: λA) заключается в построении матрицы B, элементы которой получены путём умножения каждого элемента матрицы A на это число, то есть каждый элемент матрицы B равен
bij = λaij
Сложение матриц
Сложение матриц A + B есть операция нахождения матрицы C, все элементы которой равны попарной сумме всех соответствующих элементов матриц A и B, то есть каждый элемент матрицы C равен
cij = aij + bij
Умножение матриц
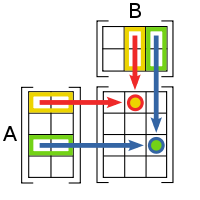
Умножение
матриц
(обозначение: AB,
реже со знаком умножения
) —
есть операция вычисления матрицы C,
элементы которой равны сумме произведений
элементов в соответствующей строке
первого множителя и столбце второго.
В
одном из множителей должно быть столько
же столбцов, сколько строк в другом.
Если матрица A
имеет размерность
,
B —
,
то размерность их произведения AB
= C
есть
.
Визначник означення та обчислення, властивості визначника.
Визначники 2 та 3 порядку
Означення.
Визначником другого порядку
називається число =x1y2–y1x2
Означення. Визначником третього порядку називається число =x1y2z3+y1z2x3+z1x2y3–z1y2x3–y1x2z3– x1z2y3
У визначнику можна визначити дві діагоналі. Головну діагональ визначника утворюють елементи а11, а22, а33. Побічну діагональ цього визначника складають елементи а13, а22, а31.
Для обчислення визначника третього порядку існує правило трикутників. Визначник є сумою 6-и добутків, з яких три беруться зі знаком „+” і три – зі знаком „–”. Зі знаком „+” береться добуток елементів головної діагоналі і добуток елементів, які знаходяться у вершинах двох трикутників з основами, паралельними головній діагоналі
* |
* |
* |
|
* |
* |
* |
зі знаком „+”. |
* |
* |
* |
|
Зі знаком „–” береться добуток елементів побічної діагоналі і добутки елементів, що знаходяться у вершинах двох трикутників з основами, паралельними побічній діагоналі
-
*
*
*
*
*
*
зі знаком „–”
*
*
*
Визначники довільного порядку
Ще таке означення визначника третього порядку : визначником третього порядку, що відповідає матриці, називається число, яке визначається рівністю де підсумовування поширюється на всі можливості перестановки j=(j1,j2,j3) других індексів. Це означення легко узагальнюється на випадок квадратної матриці довільного порядку n(n є N).
-сума добутків елементів нашої матриці,які взяті з різних рядків та різних стовпчиків ,при цьому кожен такий добуток входитьу суму зі знаком «+»,якщо кількість перестановок парна і «-»,якщо непарна.
Визначником n-го порядку, що відповідає матриці називається число, яке визначається рівністю де підсумовування поширюється на можливі перестановки j=(j1,j2 .jn) других індексів.. Використання цих властивостей дає змогу замінити обчислення визначників високих порядків за формулою на простіше.
Визначники довільного порядку: означення, властивості, розклад по рядку (стовпцю).
1
)Означення
а11
а12 … а1n
Нехай А= а21 а22 … а2n
. . . .
аi1 аi2 … аin
. . . .
аn1 аn2 … аnn
Тоді
визначник матриці det
A=
det A=∑ⁿi=1(-1)ͥ+ʲ аij Мij (ця формула являє собою правило складання визначника порядку n за елементами і-го рядка матриці А та за мінорами Мij елементів і-го стовпця, що є визначниками порядку (n-1))
або в окремому випадку для розкладання по 1-му рядку
det A = а11М11 - а12М12+…+ (-1) ⁿ+¹а1nМ1n
де Мij – визначник матриці (n-1) порядку, отриманої з матриці А викреслюванням i-го рядка й j-го стовпчика
Визначник – це сума добутків елементів матриці, які взяті з різних рядків та різних стовпчиків, при цьому кожен такий добуток входить зі знаком +, якщо перестановка парна, і зі знаком -, якщо непарна.
2)Властивості визначників:
1. Властивість рівноправності рядків та стовпців.
Транспонована матриця Аͭ матриці А- це така матриця, в якій елементи рядків є елементами стовпчиків у матриці А.
Тому 1-а властивість формулюється так: при транспонуванні величина визначника зберігається, тобто det A=det Аͭ ( це випливає з того, що розкладання визначника матриці А по першому стовпчику = розкладанню визначника матриці Аͭ по першому рядку )
2. Властивість антисиметрії при перестановці двох рядків (стовпців).
2-а властивість формулюється так: при перестановці місцями двох рядків (стовпців) визначник зберігає свою абсолютну величину, але змінює знак на протилежний
3. Лінійна властивість визначника.
Вважаємо, що деякий рядок (a1, a2, … , an) є лінійною комбінацією рядків (b1, b2, … , bn), (c1, c2, … , cn), …, (d1, d2, … , dn) з коефіцієнтами λ,μ, …,ν , якщо aj= λbj+ μcj+…+νdj для всіх j=1,2,3,..,n.
Властивість 3 можна сформулювати так: якщо у визначнику n-го порядку Δ деякий рядок (a1, a2, … , an) є лінійною комбінацією рядків (b1, b2, … , bn), (c1, c2, … , cn) з коефіцієнтами λ,μ, то Δ= λ Δ1+ μ Δ2, де Δ1 – визначник в якого і-ий рядок дорівнює
(b1, b2, … , bn), а всі інші рядки такі ж як і в Δ( аналогічно й для Δ2).
ДОВ. Для доведення розкладемо усі три визначники по і-у рядку, й побачимо, що у них всіх мінори однакові.
4. Визначник з нульовим рядком або з нульовим стовпцем дорівнює 0
ДОВ. Нехай і-ий рядок дорівнює 0 , тоді
аi1=0 аi2=0 … аin=0 , тоді detA=0
5. Множення будь-якого рядка або стовпця рівносильне множенню визначника на це саме число.
ДОВ. Помножимо будь-який рядок або стовпчик початкового визначника на число, розкладемо визначник по цьому рядку або стовпцю, винесемо це число за дужки й згорнемо вираз, що залишився в дужках, у початковий визначник.
6. Визначник з двома однаковими рядками чи стовпчиками дорівнює 0.
ДОВ. При перестановці двох однакових рядків (стовпчиків) визначник матриці змінює знак. Визначник залишиться таким самим. Виходить, що –detA=detA. Звідси випливає, що detA=0
7. Визначник, що містить два пропорційні рядки (стовпчики), дорівнює 0.
ДОВ. Винесемо коефіцієнт пропорційності за знак визначника. У ньому утворяться два однакові рядки. Тому такий визначник дорівнює 0.
8. Визначник матриці не зміниться, якщо до елементів рядка додати елементи іншого, помножені на одне й те саме число.
ДОВ. Отриманий визначник можна розкласти на суму двох визначників. Один з них є початковим, а інший містить два пропорційні рядки, отже, дорівнює 0.
9. Сума добутків елементів одного рядка (стовпця) дорівнює визначнику матриці і алгебраїчного доповнення до елементів іншого рядка цієї матриці дорівнює 0.
10. Визначник добутку квадратних матриць дорівнює добутку визначників цих матриць, тобто
detA*B=detA*detB
3) Розклад визначника по рядку (стовпцю).
* Зручно використовувати розклад по тому рядку чи стовпцю, більшість елементів якого дорівнюють 0.
Принцип:
розкладаємо за формулами (по рядку)det A=∑ⁿj=1(-1)ͥ+ʲ аij Мij
(по стовпцю)det A=∑ⁿi=1(-1)ͥ+ͥ аijМij
Наприклад розклад по 1-му рядку виглядатиме так:
det A = а11М11 - а12М12+…+ (-1) ⁿ+¹а1nМ1n
На окремому прикладі розглянемо цей принцип (розкладаємо по третьому стовпцю)
2
2 -1
det A= 2 -4 1
-2 -2 2
2
-4 2 2 2 2
det A=(-1)(-1)¹+³ -2 -2 + 1(-1) ²+³ -2 -2 +2(-1) ³ +³ 2 -4 = -(-4-8)-(-4+4)+2(-8-4)= -12