19. Розриви функції, приклади.

Пусть функция f(x) определена на некотором множестве Е и х0 – предельная точка множества Е.

Функция f(x) называется непрерывной в точке х0, если

1. Она определена в точке х0

2. Существует конечный предел

3. Этот предел равен значению функции в точке х0.

Иначе говоря, функция у=f(x) называется непрерывной в точке, если бесконечно малому приращению аргумента в этой точке соответствует бесконечно малое приращение функции, то есть

Разрывность функции

Итак, если хотя бы одно из трех условий непрерывности не выполняется, функция называется разрывной в точке х0, а сама точка x0-точкой разрыва. Если в точке x0 оба односторонних предела существуют и конечны, то разрыв называется разрывом первого рода. Пусть х0-точка разрыва первого рода, т.е.

Возможны два случая

1. f(x0+0)=f(x0-0)=L, но либо функция f(x) не определена в точке х0, либо f(x0) # L (то есть не выполнено либо первое либо третье условие непрерывности). В этом случае разрыв называется устранимым, так как если доопределить функцию в точке х0 или переопределить ее, положив f(x0)=L, функция f(x) станет непрерывной в точке х0.

оба односторонних предела существуют, конечны и равны.

2. f(x0- 0)  f(x0+0) B этом случае разрыв называется неустранимым.

Если же хотя бы один из односторонних пределов f(x0+0) или f(x0-0) не существует или бесконечен, то разрыв называется разрывом второго рода. Разрыв второго рода всегда неустранимый.

Если в точке х0 функции f(x) и g(x) непрерывны, то в этой же точке непрерывными являются и функции

Точки разрыва

Если попытаться построить отрицание свойства непрерывности функции в точке (предельной для области определения, то получится следующее:

.

Другими словами, существует такая окрестность значения функции в рассматриваемой точке, что сколь близко мы не подходили бы к данной точке, всегда можно будет найти точку, значение в которой окажется за пределами заданной окрестности.

В этом случае говорят, что функция f терпит разрыв в точке a.

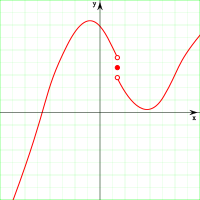
Возможны два варианта:

либо предел функции существует, но он не совпадает со значением функции в данной точке:

тогда точка a называется точкой устранимого разрыва функции f. Положив можно добиться непрерывности функции в этой точке. Такое изменение значения функции в точке, превращающее функцию в непрерывную в этой точке, называется доопределением по непрерывности.

либо предела функции в данной точке не существует и тогда

.

У числовой функции, заданной на вещественной прямой (или её подмножестве), однако, возможно существование односторонних пределов. Отсюда возникает классификация точек (неустранимого) разрыва:

если оба односторонних предела существуют и конечны, но хотя бы один из них отличен от значения функции в данной точке, то такую точку называют точкой разрыва первого рода;

если хотя бы один из односторонних пределов не существует или не является конечной величиной, то такую точку называют точкой разрыва второго рода.

20. Матриці, операції над матрицями.

Ма́трица — математический объект, записываемый в виде прямоугольной таблицы элементов кольца или поля, которая представляет собой совокупность строк и столбцов, на пересечении которых находятся её элементы. Количество строк и столбцов матрицы задают размер матрицы.

Матрицы широко применяются в математике для компактной записи систем линейных алгебраических или дифференциальных уравнений. В этом случае, количество строк матрицы соответствует числу уравнений, а количество столбцов — количеству неизвестных. В результате, решение систем линейных уравнений сводится к операциям над матрицами.

Матрицы допускают следующие алгебраические операции:

• сложение матриц, имеющих один и тот же размер;

• умножение матриц подходящего размера (количество строк одной матрицы должно совпадать с количеством столбцов другой);

• умножение матрицы на элемент основного кольца или поля (т. н. скаляр).

Относительно сложения матрицы образуют абелеву группу; если же рассматривать ещё и умножение на скаляр, то матрицы образуют векторное поле над соответствующим кольцом или полем. Для квадратных матриц матричное умножение является замкнутой операцией, поэтому квадратные матрицы одного размера образуют кольцо относительно матричного сложения и матричного умножения.

Матрица представляет собой матрицу некоторого линейного оператора: свойства матрицы соответствуют свойствам линейного оператора. В частности, собственные числа матрицы — это собственные числа оператора, отвечающие соответствующим собственным векторам.

В математике рассматривается множество различных типов и видов матриц. Таковы, например, единичная, симметричная, кососимметричная, верхнетреугольная (нижнетреугольная) и т. п. матрицы.

Особое значение в теории матриц занимают всевозможные нормальные формы. Наиболее важной (в теоретическом значении) и проработанной является теория жордановых нормальных форм. На практике, однако, используются такие нормальные формы, которые обладают, например, устойчивостью.

Сложение и вычитание допускается только для матриц одинакового размера.

Существует нулевая матрица Θ такая, что её прибавление к другой матрице A не изменяет A, то есть

A + Θ = A

Все элементы нулевой матрицы равны нулю.

Возводить в степень можно только квадратные матрицы.

• Ассоциативность сложения: A + (B + C) = (A + B) + C.

• Коммутативность сложения: A + B = B + A.

• Ассоциативность умножения: A(BC) = (AB)C.

• Вообще говоря, умножение матриц некоммутативно: 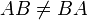. Используя это свойство, вводят коммутатор матриц.

• Дистрибутивность умножения относительно сложения:

A(B + C) = AB + AC;

(B + C)A = BA + CA.

• С учётом упомянутых выше свойств, матрицы образуют кольцо относительно операций сложения и умножения.

• Свойства операции транспонирования матриц:

(A^T)^T = A

(AB)^T = B^TA^T

(A ^{− 1})^T = (A^T) ^{− 1}, если обратная матрица A ^{- 1} существует.

(A + B)^T = A^T + B^T

detA = detA^T