10. Фундаментальність послідовності, довести фундаментальність збіжної послідовності, критерій Коші.

Фундаментальна послідовність, або сходящаяся в собі послідовність, або послідовність Коші - послідовність точок метричного простору така, що для будь-якого заданої відстані існує елемент послідовності, починаючи з якого всі елементи послідовності знаходяться один від одного на відстані не більше ніж задане.

для будь-якого   існує таке натуральне N ε , Що   для всіх n, m> N ε 

Простір, у якому кожна фундаментальна послідовність сходиться, називається повним.

Властивості

Кожна сходящаяся послідовність є фундаментальною, але не кожна фундаментальна послідовність сходиться.

Нехай   - Послідовність, що сходиться до точки a .

Фіксуємо ε> 0 .

Тоді, згідно з визначенням границі послідовності, існує такий номер   , Що для всякого n> N , Буде мати місце нерівність   .

Тепер, за нерівністю трикутника,   для будь-яких n> N і m> N , Що потрібно було показати згідно з визначенням (збіжності в собі).

Критерій Коші.

У множині дійсних чисел R послідовність збігається тоді і тільки тоді, коли вона фундаментальна.

11. Означення границі функції в точці по Коші та по Гейне.

Означення границі за Коші.

- гранична точка А. Число називається границею f(x) при , якщо .

Позначення: або .

Означення границі за Гейне.

- гранична точка А (можливо, або ).

(можливо, , або , або ), якщо , такої, що

• ;

• 

виконується .

Означення за Коші і за Гейне еквівалентні.

Зауваження: означення за Гейне застосовується для доведення того факту, що не існує.

12. Односторонні границі функції, елементарні властивості цих границь.

Нехай функція визначена на проміжку 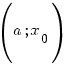. Число називають лівою границею функції в точці і пишуть

,

якщо для будь-якого числа знайдеться додатнє число , яке залежить від , таке, що для всіх , які задовільняють нерівність , виконується нерівність

.

Аналогічно визначається права границя функції . Для позначення правої границі функції в точці використовується позначення

.

Ліва і права границі функції називаються односторонніми границями.

Якщо функція визначена на проміжку , за винятком, можливо, точки , то для існування границі

необхідно і достатньо, щоб права і ліва границі функції в точці існували і були рівні:

.

13. Нескінчено малі та великі величини їх зв’язок, порівняння нескінчено малих та великих величин.

13. Змінна величина х називається нескінченно ма­лою, якщо в процесі її зміни наступить такий момент, почи­наючи з якого, абсолютна величина змінної х стає і залишаєть­ся менше будь-якого, скільки завгодно малого, наперед заданого додатного числа є, тобто .

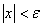Алгебраїчна сума будь-якого скінченного числа не­скінченно малих величин є величина нескінченно мала.

Доведення. Нехай задано k нескінченно малих величин α1, α2,...,αk. Доведемо, що їх алгебраїчна сума (α1 ± α2 ± ... ± αk) буде величиною нескінченно мстою. Візьмемо скільки завгодно мале > 0. Згідно з означенням нескінченно малих в процесі їх зміни наступить такий момент, починаючи з якого будуть ви­конуватися нерівності:

Звідси, використовуючи властивості модуля, одержимо:

|α1±α2+...±αk| |α1| + |α2| + ... + |αk|< + + ... + = ε

Отже, маємо: |α1±α2+...±αk| ε

Ця нерівність, згідно з означенням 1, означає, що (αl±α2±...±αk) є нескінченно малою величиною. Теорема до­ведена.

Теорема 2. Добуток обмеженої величини на нескінченно малу величину є величина нескінченно мала.

Доведення. Нехай у — обмежена величина, α — нескінченно мала. Для обмеженої величини у існує таке число М, що |у| М. Згідно з означенням нескінченно малої в процесі змінювання a наступить такий момент, починаючи з якого буде виконуватися нерівність < — для будь-якого ε > 0. Тому, починаючи з деякого моменту, буде виконуватись нерівність

Ця нерівність означає, що у-а є величиною нескінченно ма­лою, що і треба було довести.