91. Метод Остроградського інтегрування дробово-раціональної функції.

ОСТРОГРАДСКОГО МЕТОД

- метод выделения алгебраич. части у неопределенных интегралов от рациональных функции. Пусть Р(х).и Q(х).- многочлены с действительными коэффициентами, причем степень Р(х).меньше степени Q(х).и, следовательно,   -правильная дробь,

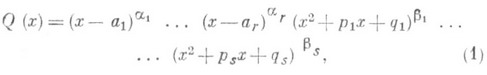
ai, pj, qj - действительные числа,   и bi- - натуральные числа, i=l, 2, ..., r, j=1, 2, ..., s,

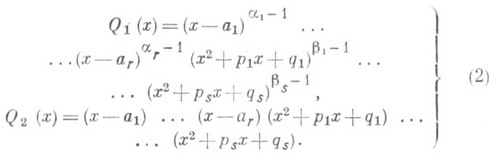
Тогда существуют такие действительные многочлены Р 1 (х).п Р 2 (Х), степени к-рых меньше соответственно чем степени п 1 и n2=r+2s многочленов Q1(x).и Q2(x), что 

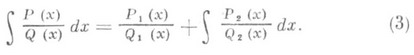
Важным является то обстоятельство, что многочлены Q1(x) н Q2(x).можно найти без знания разложения (1) многочлена Q(x).на неприводимые множители: многочлен Q1(x).является наибольшим общим делителем многочлена Q(х).и его производной Q' (х).и может быть получен с помощью алгоритма Евклида, a Q2(x)=Q(x)/Q1(x). Коэффициенты многочленов P1(x).и Р 2 (х).можно вычислить с помощью неопределенных коэффициентов метода. О. м. сводит, в частности, задачу интегрирования правильной рациональной дроби к задаче интегрирования правильной рациональной дроби, знаменатель к-рой имеет, простые корни; интеграл от такой функции выражается через трансцендентные функции: логарифмы и арктангенсы. Следовательно, рациональная дробь 

 в формуле (3) является алгебраич. частью неопределенного интеграла 

92. Обчислення інтегралу .

Интегралы типа    где а, b, с, d - действительные числа, ,,...,, - натуральные числа, сводятся к интегралам от рациональной функции путем подстановки   где К - наименьшее общee кратное знаменателей дробей 

Действительно, из подстановки   следует, что   и

т. е. х и dx выражаются через рациональные функции от t. При этом и каждая степень дроби   выражается через рациональную функцию от t.

93. Інтегрування диференціального біному.

Интегрирование дифференциального бинома

Интегралы типа(называемые интегралами от дифференциального бинома), где а, b - действительные числа; m, n, р - рациональные числа, берутся, как показал Чебишев П.А., лишь в случае, когда хотя бы одно из чисел р, (m+1)/n  или (m+1)/n+р является целым.

Рационализация интеграла в этих случаях осуществляется следующими подстановками:

1) если р - целое число, то подстановка х=tk, где k - наименьшее общее кратное знаменателей дробей m и n;

2)  если   (m+1)/n - целое число, то подстановка  где s —знаменатель дроби р;

3)  если (m+1)/n+р - целое число, то подстановка где s - знаменатель дpоби р.

Во всех остальных случаях интегралы типане выражаются через известные элементарные функции, т. е. «не берутся».

94. Очислення інтегралу .

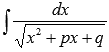, где p и q – действительные коэффициенты.

В этом случае выделяем полный квадрат под знаком корня:

и используем формулу из таблицы неопределенных интегралов  .

То есть,

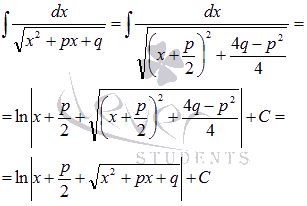
95. Очислення інтегралу .

Вычисление неопределенных интегралов типа сводится к вычислению интегралов от paциoнaльнoй фyнкции подстановкой   , которая называется универсальной.

Действительно,

 ,

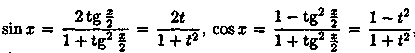Поэтому

где R₁(t) - рациональная функция от t. Обычно этот способ весьма громоздкий, зато он всегда приводит к результату.

На практике применяют и другие, более простые подстановки, в зависимости от свойств (и вида) подынтегральной фyнкции. В частнocти, удобны следующие правила:

1)  если  функция  R(sinx;cos x)   нечетна  относительно  sinx,  т.е. R(— sinx;cos x)=— R(sin x;cos x), то подстановка cosx=t рационализирует интеграл;

2)  если  функция  R(sinx;cos x)   нечетна  относительно  cosx,  т.е. R(sinx; - cosx)=—R(sinx;cosx), то делается подстановка sinx=t;

3)  если функция  R(sin x; cos x)   четна  относительно sinx   и  cosx R(— sin x; - cos x)=R(sin x; cos x), то интеграл рационализируется подстановкой tgx=t. Такая же подстановка применяется, если интеграл имеет вид