75. Достатні умови екстремуму для функції двох змінних.

Говорят, что функция   имеет максимум в точке  , т.е. при   , если   для всех точек  , достаточно близких к точке   и отличных от неё.

Говорят, что функция   имеет минимум в точке  , т.е. при  , если   для всех точек  , достаточно близких к точке   и отличных от неё.

Максимум и минимум функции называются экстремумами функции.

Теорема (необходимое условие экстремума функции двух переменных). Если функция   достигает экстремума при  , то каждая частная производная первого порядка от   или обращается в нуль при этих значениях аргументов, или не существует.

Теорема (достаточное условие экстремума функции двух переменных). Пусть в некоторой области, содержащей точку   функция   имеет непрерывные частные производные до третьего порядка включительно. Пусть, кроме того, точка   является критической точкой функции  , т.е. 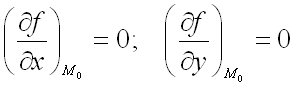, тогда при  : 1)   имеет максимум, если дискриминант   и  , где 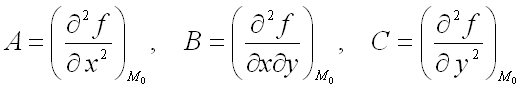 ; 2)   имеет минимум, если дискриминант   и  ; 3)   не имеет ни минимума, ни максимума, если дискриминант  ; 4) если   , то экстремум может быть, а может и не быть (требуется дополнительное исследование).

76. Умовний екстремум функція Лагранжа.

Условными экстремумами именуются условные максимум и минимум.

В случае функции двух переменных задача о нахождении точек условного экстремума решается одним из описанных ниже способов.

1. Если представляется возможным, то из уравнения связи . В результате функция преобразуется в функцию одной переменной , что даёт возможность решения задачи известными методами.

В противном случае при нахождении точек экстремума используется метод множителей Лагранжа, заключающийся в следующем.

2. Составляется функция Лагранжа

,

где . Следовательно, на выполнено и в связи с этим задача в случае двух переменных, также как и в п. 1, сокращается до поиска экстремума функции одной переменной x.

Формально процедура решения выглядит следующим образом. Сначала необходимо приравнять к нулю все частные производные функции Лагранжа:

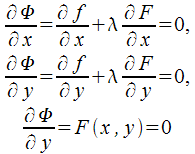
И отсюда можно найти решение { }.

Пусть — любое из решений этой системы.

Подставляя в дифференциал найденный из уравнения связи, и посредством обозначения, имеем . Тогда, если имеет в т. условный максимум, если — то условный минимум.

77. Знаходження максимального та мінімального значення в області.

78. Первісна функції означення основні властивості.

Первообра́зной [1] или примити́вной функцией (иногда называют также антипроизводной) данной функции f называют такую F, производная которой (на всей области определения) равна f, то есть F ′ = f. Вычисление первообразной заключается в нахождении неопределённого интеграла, а сам процесс называется интегрированием.

Так, например, функция является первообразной . Так как производная константы равна нулю, будет иметь бесконечное количество первообразных; таких как или … и т. д.; таким образом семейство первообразных функции x2 можно обозначить как F(x) = x3 / 3 + C, где C — любое число. Графики таких первообразных смещены вертикально относительно друг друга, и их положение зависит от значения C.

Свойства первообразной

Первообразная суммы равна сумме первообразных

Первообразная произведения константы и функции равна произведению константы и первообразной функции

Достаточным условием существования первообразной у заданной на отрезке функции f является непрерывность f на этом отрезке

Необходимыми условиями существования являются принадлежность функции f первому классу Бэра и выполнение для неё свойства Дарбу

У заданной на отрезке функции любые две первообразные отличаются на постоянную.