Рівняння прямої у просторі як перетин площин, канонічне рівняння прямої.
Каноническое
уравнение получается из параметрическиx
уравнений делением одного уравнения
на другое:
где
— координаты Х и У направляющего вектора
прямой, Х0 и У0 координаты точки,
принадлежащей прямой.
Общее векторное уравнение прямой в пространстве:
Поскольку прямая является пересечением двух различных непараллельных плоскостей, заданных соответственно общими уравнениями:
и
то
уравнение прямой можно задать системой
этих уравнений:
Взаємне розміщення прямої та площини у просторі.
Прямая может лежать на данной плоскости, быть параллельна данной плоскости или пересекать ее в одной точке, см. следующие рисунки.
рис.6.
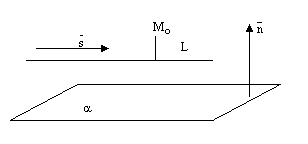
рис.7.
рис.8.
Теорема.
Пусть плоскость 
задана
общим уравнением
,
а прямая L задана каноническими уравнениями
или параметрическими уравнениями
, 
,
в
которых 
– координаты нормального вектора плоскости
, 
– координаты произвольной
фиксированной точки прямой L, 
–
координаты направляющего вектора прямой L. Тогда:
1)
если 
,
то прямая L пересекает плоскость
в
точке,координаты которой 
можно
найти из системы уравнений
;
(7)
2)
если 
и 
,
то прямая лежит на плоскости;
3)
если
и 
,
то прямая параллельна плоскости.
Доказательство.
Условие 
говорит
о том, что вектроры 
и 
не
ортогональны, а значит прямая не
параллельна плоскости и не лежит в
плоскости, а значит пересекает ее в
некоторой точке М. Координаты точки
М удовлетворяют как уравнению плоскости,
так и уравнениям прямой, т.е. системе
(7). Решаем первое уравнение системы (7)
относительно неизвестной t и затем,
подставляя найденное значение t в
остальныеуравнения системы,
находим координаты искомой
точки.
Если 
,
то это означает, что 
.
А такое возможно лишь тогда, когда прямая
лежит на плоскости или параллельна ей.
Если прямая лежит на плоскости, то любая
точка прямой является точкой плоскости
икоординаты любой
точки прямой удовлетворяют уравнению
плоскости. Поэтому достаточно проверить,
лежит ли на плоскости точка
.
Если
,
то точка 
–
лежит на плоскости, а это означает, что
и сама прямая лежит на плоскости.
Если , а , то точка на прямой не лежит на плоскости, а это означает, что прямая параллельна плоскости.
Теорема доказана.
Криві другого порядку вивід рівняння еліпса, основні параметри еліпса.
Э́ллипс— геометрическое место точек M Евклидовой плоскости, для которых сумма расстояний до двух данных точек F1 и F2 (называемых фокусами) постоянна и больше расстояния между фокусами, то есть
| F1M | + | F2M | = 2a, причем | F1F2 | < 2a.
Окружность является частным случаем эллипса. Наряду с гиперболой и параболой, эллипс является коническим сечением и квадрикой. Эллипс также можно описать как пересечение плоскости и кругового цилиндра или как ортогональную проекцию окружности на плоскость.
Отрезок AB, проходящий через фокусы эллипса, концы которого лежат на эллипсе, называется большой осью данного эллипса. Длина большой оси равна 2a в вышеприведённом уравнении.
Отрезок CD, перпендикулярный большой оси эллипса, проходящий через центральную точку большой оси, концы которого лежат на эллипсе, называется малой осью эллипса.
Отрезки, проведённые из центра эллипса к вершинам на большой и малой осях называются, соответственно, большой полуосью и малой полуосью эллипса, и обозначаются a и b.
Точка пересечения большой и малой осей эллипса называется его центром.
Точки пересечения эллипса с осями являются его вершинами.
Расстояния r1 и r2 от каждого из фокусов до данной точки на эллипсе называются фокальными радиусами в этой точке.
Расстояние
называется фокальным расстоянием.
Диаметром называют произвольную хорду, проходящую через его центр. Сопряжёнными диаметрами называют пару его диаметров, обладающих следующим свойством: середины хорд, параллельных первому диаметру, лежат на втором диаметре. В этом случае и середины хорд, параллельных второму диаметру, лежат на первом диаметре.
Эксцентриситетом
эллипса называется отношение
.
Эксцентриситет (также обозначается ε)
характеризует вытянутость эллипса. Чем
эксцентриситет ближе к нулю, тем эллипс
больше напоминает окружность и наоборот,
чем эксцентриситет ближе к единице, тем
он более вытянут.
Фокальным
параметром
называется половина длины хорды,
проходящей через фокус и перпендикулярной
большой оси эллипса.
Отношение
длин малой и большой полуосей называется
коэффициентом сжатия эллипса или
эллиптичностью:
.
Величина, равная
называется сжатием эллипса. Для окружности
коэффициент сжатия равен единице, сжатие
— нулю. Коэффициент и эксцентриситет
эллипса связаны соотношением
Каноническое уравнение
Для любого эллипса можно найти декартову систему координат такую, что эллипс будет описываться уравнением (каноническое уравнение эллипса):
Оно
описывает эллипс с центром в начале
координат, оси которого совпадают с
осями координат. Для определённости
положим, что
В этом случае величины a
и b
— соответственно, большая и малая
полуоси эллипса.
Зная полуоси эллипса можно вычислить его фокальное расстояние и эксцентриситет:
Координаты фокусов эллипса:
Эллипс имеет две директрисы, уравнения которых можно записать как
Фокальный параметр (т.е. половина длины хорды, проходящей через фокус и перпендикулярной оси эллипса) равен
Фокальные
радиусы, т. е. расстояния от фокусов до
произвольной точки кривой
Уравнение диаметра, сопряжённого хордам с угловым коэффициентом k:
Уравнение
касательных, проходящих через точку
Уравнение касательных, имеющих данный угловой коэффициент k::
Уравнение нормали в точке
