Розв’язність системи лінійних однорідних рівнянь, представлення загального розв’язку .
1)Загальні поняття системи лінійних рівнянь.
Система m лінійних рівнянь із n змінними має вигляд
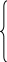
a11x1+a12x2+…+a1nxn=b1
a21x1+a22x2+…+a2nxn=b2 (1)
…………………….
am1x1+am2x2+…+amnxn=bm
або в скороченому записі
∑ⁿj=1 аijхi= bi, і=1,2,…,m
Невідомі – величини хj (змінні), які підлягають визначенню.
Коефіцієнти при змінних - аij
Вільні члени рівнянь - bi
Розв’язок системи – впорядкована сукупність чисел α1, α2,…, αn, що при підстановці в систему перетворює кожне рівняння в тотожність.
Сумісна система – система рівнянь, якщо має хоч один розв’язок, а несумісна – якщо немає розв’язків.
Визначена система - має єдиний розв’язок, невизначена - більше одного розв’язку.
Рівносильні системи – якщо множини розв’язків співпадають.
Системи зручно розв’язувати в матричній формі:
а11
а12 … а1n
х1 b1
А= а21 а22 … а2n ; Х= х2 ; B= b2
. . . . . .
аm1 аm2 … аmn хm bm
або А·Х=В
2) Однорідні системи лінійних рівнянь.
Однорідні системи лінійних рівнянь – система, при якій всі вільні члени дорівнюють нулю
a11x1+a12x2+…+a1nxn=0
a21x1+a22x2+…+a2nxn=0
…………………….
am1x1+am2x2+…+amnxn=0
або А·Х=0
Властивості однорідної системи лінійних рівнянь:
однорідна система завжди сумісна ,тому що завжди має, щонайменше нульовий розв’язок.
Для існування ненульових розв’язків ранг матриці коефіцієнтів повинен бути менше числа змінних r<n, тобто число лінійно незалежних рівнянь повинне бути менше числа змінних. У цьому випадку detA=0
Якщо матриця-стовпець (вектор)
х11
е= х21 є розв’язком системи лінійних рівнянь (1), то стовпчик
.
хm1
λ х11
е’=λ·е= λ х21 також є розв’язком цієї системи.
.
λ хm1
Нехай е – розв’язок системи. Тоді матричне рівняння при підстановці х=е’ перетворюється в тотожність А·е’=0.Тоді знайдемо добуток матриць А і λ·е:
А· (λ·е)= λ · (А·е)= λ·0. Звідси стовпець е’= λ·е також є розв’язком матричного рівняння.
Якщо матриці-стовпці
х11 х12
е1= х21 та е2= х22 є розв’язками системи (1), тобто А·е1=0 і А·е2=0,
. .
х m1 хm2
то й стовпець е= λ1·е1+ λ2·е2, де λ1 ,λ2 – довільні числа, також є розв’язком системи А·е=0
ДОВ. для доведення перемножимо матриці А і е = λ1·е1+ λ2·е2:
А(λ1·е1+ λ2·е2)= λ10+ λ20=0. Отже будь-яка лінійна комбінація розв’язків однорідної системи лінійних рівнянь також є розв’язком цієї системи.
3) Загальний розв’язок системи неоднорідних лінійних рівнянь.
ТЕОРЕМА(про загальний розв’язок системи неоднорідних лінійних рівнянь)
Загальний розв’язок системи лінійних рівнянь із n змінними дорівнює сумі загального розв’язку відповідної їй системи однорідних рівнянь і деякого часткового розв’язку початкової системи.
ДОВ.
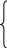
a11x1+a12x2+…+a1nxn=b1
a21x1+a22x2+…+a2nxn=b2 Запишемо розширену матрицю
…………………….
am1x1+am2x2+…+amnxn=bm
a11 a12 … a1n b1
a21 a22 … a2n b2
………………… . Використовуючи елементарні перетворення , приведемо її до
am1 am2 … amn bm східчастого вигляду:
a11 a12 … а1r … a1n b1 Зрозумівши, що система має розв’язки, методом Гаусса
0 a22 … а2r … a2n b2 знайдемо послідовно змінні хr, хr-1, х1, виражені через
… … … … … … … вільні змінні хr+1,хr+2 ,хn. Вільні змінні позначимо через с…
0 0 … аrr … аrn br В результаті отримаємо розв’язок у загальному вигляді:
0 0 … 0 … 0 br+1
0 0 … 0 … 0 0
… … … … … ... …
0 0 … 0 … 0 0
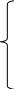x1=
х11с1+х12с2+…+ x1,
n-r
c
n-r
+ b1
x2= х21с1+х22с2+…+ x2, n-r c n-r + b2
…………………………………..
xr= хr1с1+хr2с2+…+ xr, n-r c n-r + br
xr+1=c1
…….
xn= c n-r
Запишемо розв’язок у матричній формі:
x
1 х11 х12
x1,
n-r b1
x2 х21 х22 x2, n-r b2
… … … … …
xr = с1 хr1 + с2 хr2 + …+ c n-r xr, n-r + br
xr+1 1 0 0 0
… … … … …
xn 0 0 1 0
або в скороченій матричній формі х=е1с1+е2с2+…+еrсr+b, де х, е1, е2, …, еr, b – відповідні матриці-стовпці (вектори). Лінійна комбінація е1с1+е2с2+…+еrсr є загальним розв’язком системи, а вектор b – частковим розв’язком