Метод Крамера розв’язування системи лінійних рівнянь.
(1)
Теорема (правило Крамера):
Позначимо
,
Якщо
,
то система має єдиний розв’язок, який
рахується за формулою
.
Доведення:
Для
:
Помножимо кожне i-те рівняння з системи (1) на Ai1, а потім додамо всі рівняння. Отримаємо:
(2)
З
того, що сума елементів i-го
стовпчика, помножених на алгебраїчні
доповнення до елементів j-го
стовпчика (
)
дорівнює нулю, отримуємо, що л.ч. (2)
дорівнює визначнику матриці
,
тобто
.
Тоді
і
.
Аналогічно для інших xi.
Евклідовий n-мірний простір, операції над векторами, скалярний добуток.
Евклідів простір — скінченновимірний дійсний векторний простір L з симетричним, скалярним добутком[1]. Характеристики евклідового простору неформально можна вважати узагальненнями звичних та досліджуваних Евклідом2- та 3-вимірних просторів.
Евклідова метрика
Нехай декартові координати в тривимірному просторі такі, що якщо точці P відповідають три її координати (x1, x2, x3), а точці Q -- координати (y1, y2, y3). Тоді, якщо квадрат довжини прямолінійного відрізку, що з'єднує P та Q дорівнює: l2 = (x1 - y1)2 + (x2 - y2)2 + (x3 - y3)2, то такий простір називають евклідовим простором, а декартові координати з такими властивостями називають евклідовими координатами.
Узагальнюючи
на випадок n
вимірів, отримаємо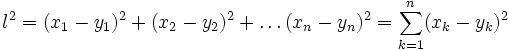 
.
Функція відстані між двома точками має назву метрики, а наведений вище вид такої функції для евклідового простору має назву евклідової метрики.
Вектори в евклідовому просторі
З точками евклідового простору зручно зіставляти вектори. Назвемо вектор, направлений від початку координат у точку P радіус-вектором цієї точки. Декартові координати (x1, x2, x3) точки Р будемо називати координатами радіус-вектора. Два вектори, які направлені з початку координат до точок P та Q з координатами p= (x1, x2, x3) та q= (y1, y2, y3) можна складати покоординатно. Тобто отримати вектор p+q з координатами (x1 + y1, x2 + y2, x3 + y3).
Можна також домножити вектор на число (скаляр). Одиничні вектори e1 = (1, 0, 0), e2 = (0, 1, 0), e3 = (0, 0, 1) мають довжину, яка дорівнює 1, а самі вектори взаємоперпендикулярні.
Будь-який
вектор v (x1,
x2,
x3)
може бути розкладений по одиничних
векторах: v = e1x1 + e2x2 + e3x3.
Тут простір тривимірний. Для n-вимірного
простору все аналогічно. Тому евклідів
простір визначається також як лінійний
(векторний) простір, в якому квадрат
відстані між точками (кінцями
радіус-векторів) визначається за
формулою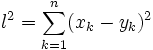 
Дія на векторами
I.Сумою
+
двох векторів
та
е вектор,що йде з початку вектора
в кінець вектора , за умови, що кінець вектора суміщений з початком вектора
+
1)a+b=b+a
2)a+(b+c)=(a+b)+c
3)0+a=a+0=a
4)a ! –a: a+(-a)=0=-a+a
II.Множення на число
Якщо - деяке число, то вектор а колінеарний з а (паралельний йому), довжина |а|=|||а|- і вектор а спів-направлений з а, якщо 0 і протилежно направлений якщо <0.
1) (a+b)= a+b
2) (a)=()a
3) (+)a=a+a
III.Дії над декартовими координатами вектора.
Нехай вектор а має координати (х1,у1), вектор b - координати(х2,у2)
тоді:
вектор а+b має координати (х1+х2,у1+у2);
вектор а має координати (х1, у1);
Це і зумовлює вищезазначені властивості.
ІV.Ділення відрізка у заданому відношенні
М(х,у)
- точка що поділяє відрізок М1М2 -
М1(х1,у1),М2(х2,у2) у заданому співвідношенні
=
:
