2.1.3 Структури.

Структура - це єдиний об'єкт, що складається із сукупності інших об'єктів, називаних компонентами.

Компоненти у свою чергу можуть бути також структурами.

Структура data:

Назва структури стоїть перед дужками, а компоненти усередині дужок, через кому.

Назва структури - ФУНКТОР.

Структури можна зображати у вигляді дерев:

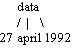
Структура з компонентами - структурами owns(bob, book(moby_dick, mell_will)).

Структури можна використовувати для представлення геометричних фігур.

Об'єкти:

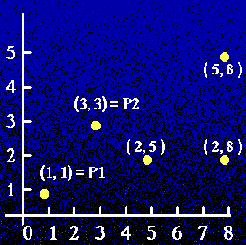
крапка Р1=point(1, 1)

крапка Р2=point(3, 3)

відрізок seg(P1, P2)

або seg(point(1, 1), point(3, 3))

трикутник triangle(point(2, 5), point(2, 8), point(5, 8))

Структуру можна представити у вигляді дерева

Корінь дерева - головний функтор.

Якщо крапка тривимірного простору: point3(X, Y, Z)

Можна записати : point(X, Y, Z)

Виходить: point(X, Y, Z) і point(X, Y)

Це різні терми, тому що кожний функтор розрізняється двома параметрами:

• ім'ям

• арністю - тобто числом атомів

Тому пишуть:

point/2

point/3

Наприклад, якщо написано: Відношення point/2 задано.

Це означає, що задано point(_,_), а не point/2(_,_).

Це типова помилка.

2.1.4 Оператори - теж функтори.

Деякі функтори зручніше записувати, як оператори.

Наприклад, можна записати +(1, 2) або

Зручніше записати 1+2 , тобто у вигляді оператора. Причому треба розуміти, що це не операція додавання, а операторний запис структури. Такі оператори називаються інфіксним.

Аналогічно операторний запис

2*a+b*c

може бути представлений у вигляді структури:

+( *(2, a), *(b, c))

Це і робить пролог при трансляції операторних виразів. Треба чітко розуміти, що оператори - це інша форма запису структури.

2.2 Арифметика.

У пролозі виконуються наступні операції:

+ – додавання; - – віднімання; * – множення; / – ділення; mod - залишок від цілочисельного розподілу.

Якщо записати:

?-X = 2+1.

X=2+1

так як. це просто співставлення змінної і структури.

Щоб арифметичний вираз розраховувався, необхідно використовувати вбудований оператор is, що змушує виконувати арифметичні операції.

?-X is 2+1.

X=3

?-Y is 2*(5+6).

Y=22

Можуть бути змінні, але вони повинні мати значення до моменту обчислення.

f(X, Y, Z):-Z is X*X + Y*Y.

і поставити запитання

?- f(2, 3, R).

R=13

Якщо визначити:

sum(X1, X2, X):-X is X1 + X2.

?-sum(2, 3, X).

X=5

?- sum(1, 1, X1), sum(X1, X1, X).

4.

2.3 Операції порівняння.

Використовуються при порівнянні чисел

Є операції

X > Y

X < Y

X >= Y

X =< Y

рівність для будь-яких термів

X = Y

X \= Y

(з побічним ефектом)

?- 100 > 4.

yes

age(mary, 20).

age(ann , 23).

age(bob , 25).

?- age(X , Y), Y>21.

X=ann;

X=bob;

?- age(X , Y), Y>21, Y<=23.

X=ann;

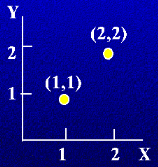
Визначимо відношення "вище" higher/2

higher(point(X1, Y1), point(X2, Y2):-Y1>Y2.

?- higher(point( 1, 1), point( 2, 2).

no

Якщо навпаки - то буде yes.

2.4 Співставлення.

Головною операцією в процесі виконання пролог -програми, є співставлення (співставлення, уніфікація) термів.

Наприклад,

рarent(pam, bob).

?- parent(pam, bob).

Yes

Ціль співставиться.

?-parent(pam, X).

X=bob

Теж співставиться, але X конкретизується і приймає значення bob

Але якщо взяти дві складових терму -структури.

a(b, C, d(e, F, g(h, i, J)))

a(B, c, d(E, f, g(H, I, j)))

чи співставляться вони? Що буде з змінними після співставлення? Як вони будуть конкретизовані?

Співставлення - це процес, на вхід якого подаються два терми, а він перевіряє, чи відповідають ці терми один одному.

Якщо терми не співставні, значить співставлення зазнає невдачі.

Якщо терми співставні, тоді процес співставлення знаходить конкретизацію змінних, що роблять ці терми тотожними, і завершується удачею.

Які ж правила визначають співставність двох термів S і Т ?

1. Якщо S і Т константи , то S і Т співставні, тільки, якщо вони є тим самим об’єктом.

Тобто:

2 зіставляється з 2

bob зіставляється з bob

2. Якщо S змінна, а Т - довільний об'єкт, то не співставні і S приписується значення T. Навпаки, якщо Т -змінна, а S - довільний об'єкт, то T приписується значення S.

Говорять, що T конкретизується значенням S. Тобто:

data(M, D, 1992).

data(may, 3, Y).

Порівнянно, змінні конкретизуються:

М=may

D=3

Y=1992

в обох термах.

3. Якщо S і Т - структури, то вони співставні, якщо

а) S і Т мають однаковий головний функтор і

b) всі їхні відповідні компоненти співставні.

Результуюча конкретизація визначається співставленням компонентів.

Якщо зіставити структури

a(b, C, d(e, F, g(h, i, J)))

a(B, c, d(E, f, g(H, I, j)))

то одержимо

B=b

C=c

E=e

F=f

H=h

I=i

J=j

Розглянемо більш складний приклад:

triangle(point(2, 5), A, point(B, 8))

triangle(X, point(2, 8), point(5, 8))

Після конкретизації

X=point(2, 5)

A=point(2, 8)

B=5

Ще один приклад:

конкретизована змінна Х=2

triangle(point(X, 5), point(X, 8), point(5, Z))

неконкретизована змінна Y=2

triangle(point(2, 5), point(Y, 8), point(5, A))

Якщо Y являє собою неконкретизовану перемінну, а змінна X конкретизовану, тоX і Y співставляються і приймає значення Х. Тобто

X=2

Y=2

Змінні Z і A обидві не конкретизовані. Вони співставляться і стають зчепленими.

Якщо дві змінні зчеплені, то при конкретизації однієї з них, другий змінної автоматично буде присвоєно теж саме конкретне значення, що і першій. Як це було з X і Y.

2.5 Друге значення операції = у Пролозі.

У пролозі операція = , крім порівняння виконує співставлення двох термів, з конкретизацією змінних.

Якщо терми співставляться, то результат істина.

?-a(B,c(x,D))=a(d,c(X,3)).

Yes

B=d

X=x

D=3

Аналогічно, /= дає істину, якщо терми не співставляться.

?-a(x)/=a(d).

Yes

2.6 Приклади співставлення структур.

Розглянемо структури, що описують відрізки.

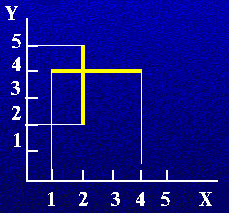
Два факти , що описують властивість вертикальність і горизонтальність.

vertical(seg(point(X,Y),point(X,Y1))).

horiz(seg(point(X,Y),point(X1,Y))).

?-vertical(seg(point(2,2),point(2,5))).

Yes

?- horiz(seg(point(1,4),point(2,4))).

Yes

?-horiz(seg(point(1,4),point(2,X))).

X=4