Отчет о выполненной работе должен содержать:

1. Тему и цель работы

2. Индивидуальное задание согласно варианту

3. Формализацию транспортной задачи

4. Решение транспортной задачи с помощью Excel и MathCAD.

5. Решение транспортной задачи любого языка программирования (листинг программы и результат ее выполнения)

6. Выводы по результатам выполнения лабораторной работы

Вопросы к защите лабораторной работы:

1. Общая математическая постановка транспортной задачи.

2. Открытая и закрытая транспортная задачи.

3. Особенности транспортных задач.

4) Методы поиска опорного плана транспортных задач: метод северо-западного угла, метод наименьших стоимостей.

5) Метод потенциалов для решения транспортной задачи.

Литература:

1. Математичні методи дослідження операцій. Навч. посібник // В.П.Лавренчук, М.І. Букатар, Т.І. Готинчан, Г.С.Пасічник. – Рута, 2008. – 360с. С.136-176;

2. Наконечний С. І., Савіна С. С. Математичне програмування: Навч. посіб. — К.: КНЕУ, 2003. — 452 с. С.184-251;

3. Охорзин В.А. Оптимизация экономических систем. Примеры и алгоритмы в среде Mathcad: Учеб. пособие. М.: Финансы и статистика, 2005. – 144 с.

4. Охорзин В.А. Прикладная математика в системе Mathcad: Учеб. пособие. Спб.: Издательство «Лань», 2008. – 352 с.

5. Кулян В. Р., Юнькова Е. А., Жильцов А. Б. Математическое программирование с элементами информационных технологий. — К.: МАУП, 2000. — 124 с.

6. Кутковецький В.Я. Дослідження операцій: Навчальний посібник. – Миколаїв: Вид-во МДГУ ім. П. Могили, 2003. – 260 с. С.102-128;

7. Исследование операций в экономике : Уч.пособие для вузов /Н.Ш.Кремер, Б.А.Прутко, И.М.Тришин, М.Н.Фридман; Под ред. Н.Ш.Кремера. — М.:ЮНИТИ, 2003. – 407 с. С.123-152;

8. Таха Х. Введение в исследование операций. — 6-е изд.: Пер. с англ. — М.: Изд. дом “Вильямс”, 2001. — 912 с. С.193-242;

9. Шикин Е.В., Шикина Г.Е. Исследование операцій: ученик. – М.: ТК Велби, Изд-во Проспект, 2006. – 280 с. С.93-113;

10. Акулич И. Л. Математическое программирование в примерах и задачах. — М., 1986. — 319 с. С.134-174;

11. Лунгу К.Н. Линейное программирование . Руководство к решению задач. – М.: ФИЗМАТЛИТ, 2005. – 128 с. С.85-110;

12. Линейное программирование/ Ашманов С.А. – М.: Наука, 1981. – 340 с. С.217-237.

13. Грешилов А.А. Прикладные задачи математического программирования: Учебное пособие. – М.: Логос, 2006. – 288 с. С.66-74,

14. Вентцель Е. С. Исследование операций. — М.: Сов. радио, 1972. —552 с. С.83-119.

Лабораторная работа №6. Решение задач нелинейного программирования

Цель работы: нахождение оптимальных решений задач нелинейного программирования графическим методом

Задание:

1. Решить задачи нелинейного программирования согласно варианта графическим методом.

Варианты задания

Варианты заданий

Вариант	Задание 1	Задание 2
1	1	2
2	2	3
3	3	4
4	4	5
5	5	6
6	6	7
7	7	8
8	8	9
9	9	1
10	1	2
11	2	3
12	3	4
13	4	5
14	5	6
15	6	7
16	7	8
17	8	9
18	9	2
19	1	3
20	2	4
21	3	5
22	4	6
23	5	7
24	6	8
25	7	9
26	8	1
27	9	2
28	1	3
29	2	4
30	3	5

1. Найти максимальное и минимальное значения функции F

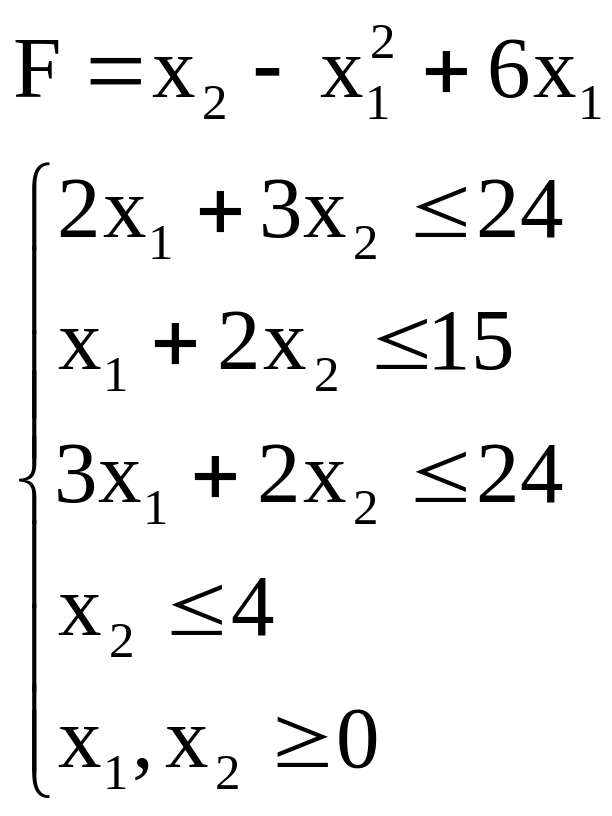
2. Найти максимальное и минимальное значения функции F

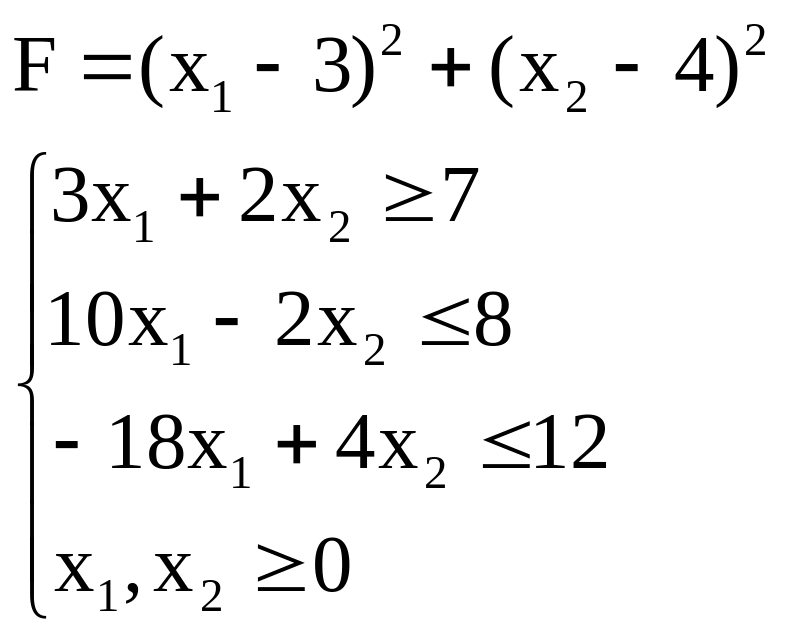
3. Найти максимальное и минимальное значения функции F

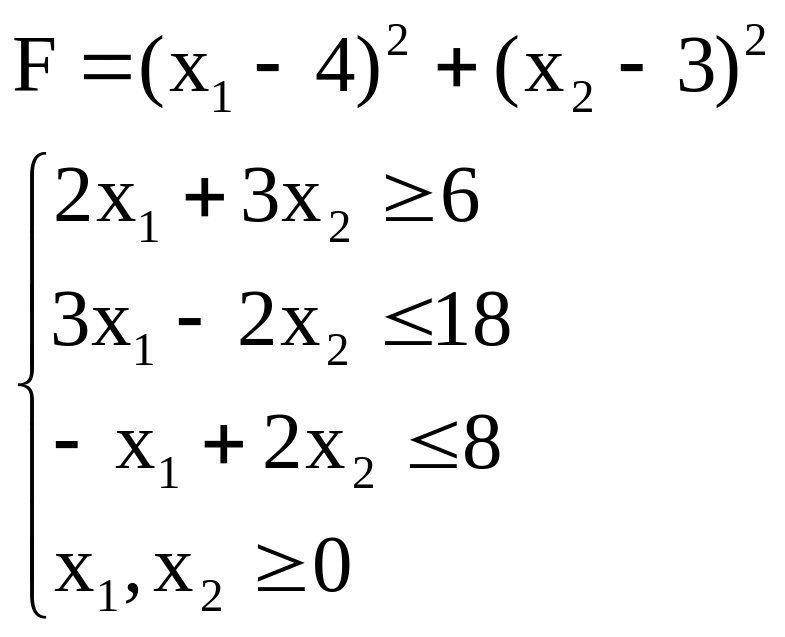
4. Найти максимальное и минимальное значения функции F

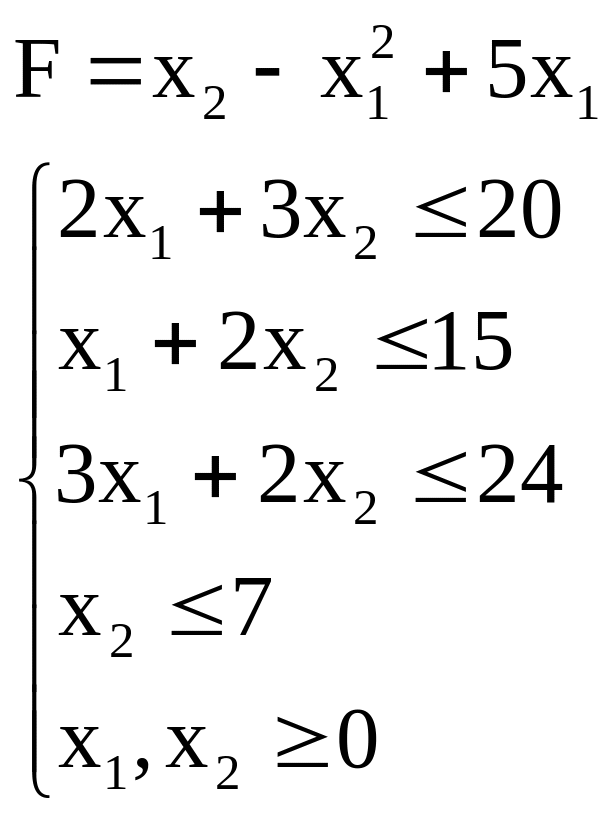
5. Найти максимальное и минимальное значения функции F

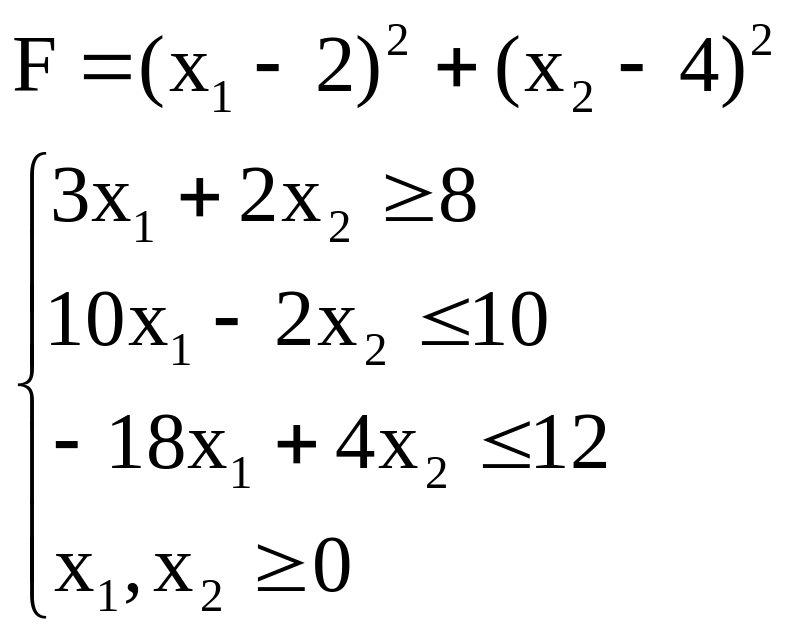
6. Найти максимальное и минимальное значения функции F

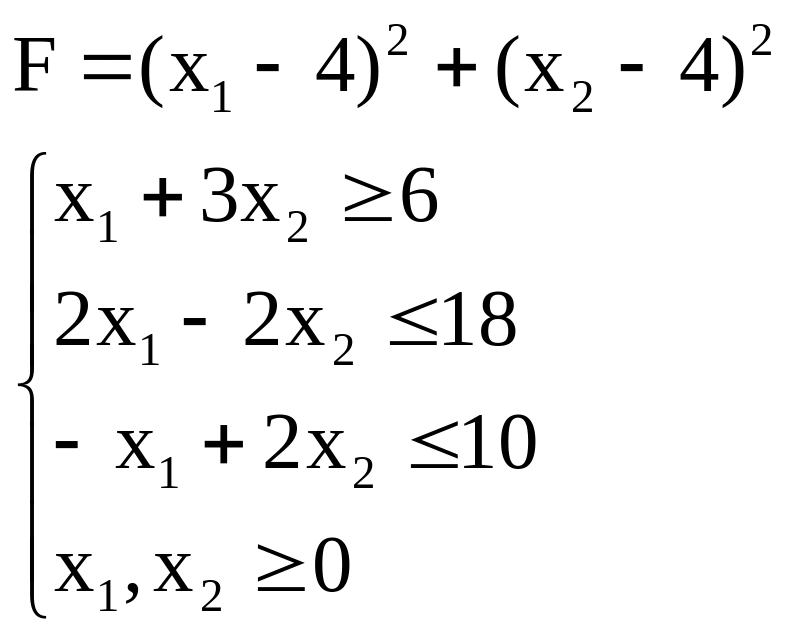
7. Найти максимальное и минимальное значения функции F

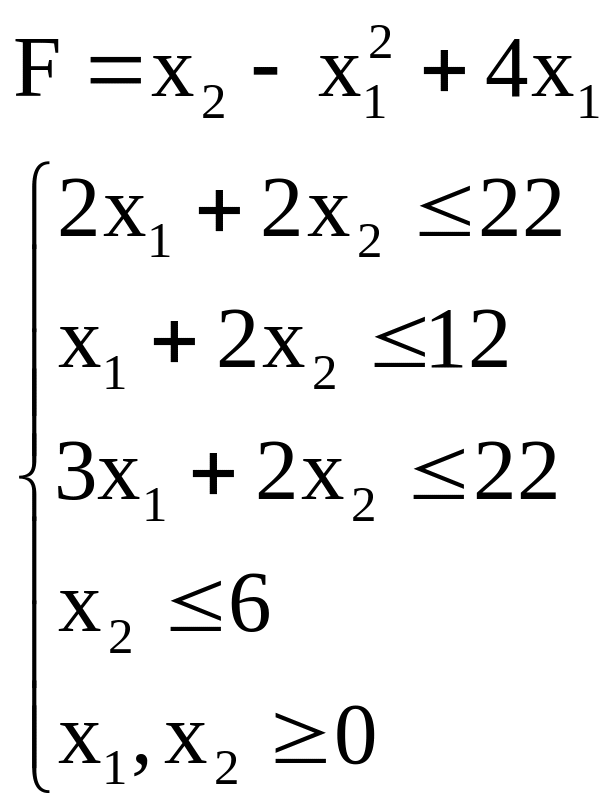
8. Найти максимальное и минимальное значения функции F

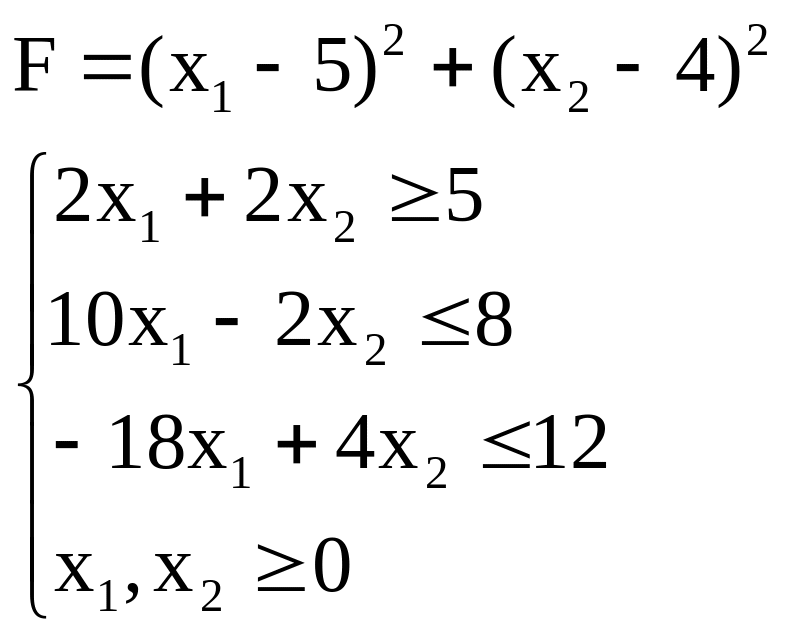
9. Найти максимальное и минимальное значения функции F

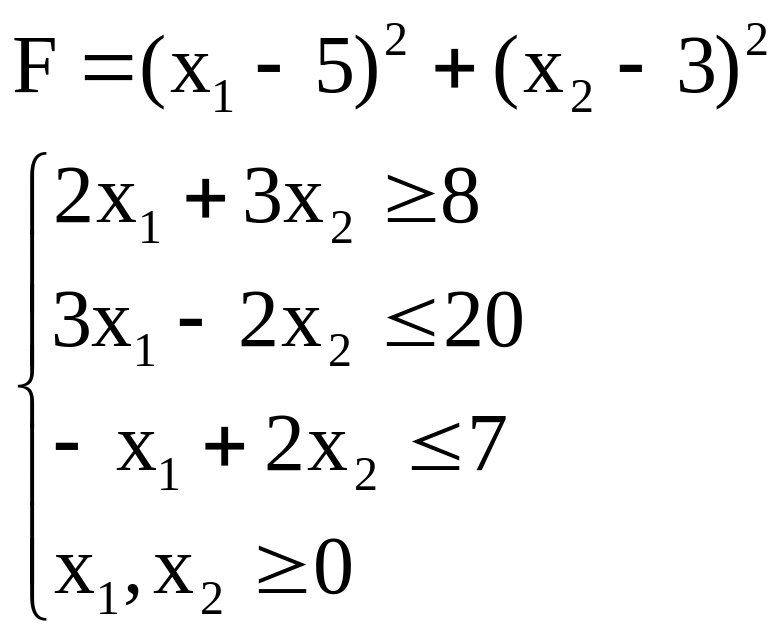
Отчет о выполненной работе должен содержать:

1. Тему и цель работы

2. Индивидуальное задание согласно варианту

3. Формализацию задачи

4. Решение задачи нелинейного программирования графическим методом.

5. Выводы по результатам выполнения лабораторной работы

Вопросы к защите лабораторной работы:

1. Понятие нелинейного программирования.

2. Графическое решение задач НЛП.

3. Градиентный метод решения задач нелинейного программирования.

Литература:

1. Экономико-математические методы и прикладные модели / Под ред. В.В.Федосеева. – М.:ЮНИТИ, 2000. – С.102-127

2. Бережная Е.В. Математические методы моделирования экономических систем. – М.: ФиС, 2006. –с.346-374

3. Грешилов А.А. Прикладные задачи математического программирования. – М.: Логос, 2006 –с.75-93

4. Вентцель Е.С. Исследование операций. – М.: Высш.школа , 2002, - с.120-177