6. Графическое решение задачи линейного программирования с двумя переменными.

Наиболее простым и наглядным методом линейного про­граммирования является графический метод. Он применяется для решения задач ЛП с двумя переменными, заданными в не­канонической форме, и многими переменными в канонической форме при условии, что они содержат не более двух свободных переменных.

Ищется такая угловая точка или набор точек из допустимого множества решений, на котором достигается самая верхняя (нижняя) линия уровня, расположенная дальше (ближе) остальных в направлении наискорейшего роста.

1. Составляется система ограничений и целевая функция.

2. Система ограничений приводится к канонической форме.

3. Строятся прямые и определяются ОДР.

Область допустимых решений – пересечение полуплоскостей системы ограничений и условий неотрицательности переменных.

4. Строится линия уровня.

Целевая функция, Z – любое значение – уравнение линии уровня.

Все линии уровня при различных значениях Z || между собой.

5. Строится вектор-градиент.

- Вектор-градиент ┴ линии уровня.

- Определение направления градиента:

А)

Б) С помощью другого значения Z построим еще одну линию уровня.

По взаимному расположению линий уровня определить направление возрастания.

6. Оптимальное решение.

Перемещая линию уровня по направлению вектора-градиента до последнего соприкосновения с ОДР, находим точку min/ max.

7 . Возможные варианты графического решения b

1 ) ОДР огранич., выпукл.

а) оптимальное решение в точке. В – точка max

б 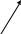) оптимальное решение достигается на отрезке. C

В С – оптимальное решение

2) ОДР неогр., выпукл. с конечны числом вершин:

а) оптимальное решение достигается в точке В

б) оптимальное решение достигается на отрезке AB

в) оптимального решения нет, целевая функция не ограничена

а)

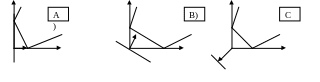
3) ОДР точка 4) ОДР пустое множество

8. Определения n-мерного пространства.

Определение 5. Точка А называется внутренней точкой вы­пуклой области, если в сколь угодно малой окрестности этой точки содержатся только точки этой области.

Определение 6. Точка В называется граничной точкой вы­пуклой области, если в сколь угодно малой окрестности этой точки содержатся как точки данной области, так и не принад­лежащие ей (рис. 19.3).

Определение 7. Точка С называется угловой точкой вы­пуклой области, если она является граничной и не лежит внутри отрезка, соединяющего две другие точки этой облас­ти (рис. 19.3).

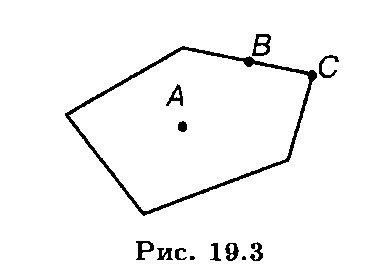
Определение 8. Если область включает все свои граничные точки, то она называется замкнутой.

Выпуклая область может быть ограниченной и неограни­ченной.

Определение 9. Ограниченной называется область, если су­ществует такое число М > 0, что радиус-вектор , соединяю­щий начало координат с любой точкой области, по абсолютной величине меньше М, т.е. || ≤ М.

Для этой области все ее точки находятся на конечном рас­стоянии от начала координат.

Определение 10. Если найдутся точки области, сколь угод­но удаленные от начала координат, то область называется не­ограниченной.

Определение 11. Выпуклая замкнутая ограниченная область, имеющая конечное число угловых точек, называется вы­пуклым п-мерным многогранником.

Определение 12. Выпуклая замкнутая неограниченная об­ласть, имеющая конечное число угловых точек, называется вы­пуклой п-мерной многогранной областью.