34. Особенности многошаговых задач, решаемых методом динамического программирования. Принцип оптимальности р. Беллмана.

Схема процесса принятия решений:

ч/з x (x1, x2, ... , xn) – обозначаются шаговые управления

S - система: S0 – начальная система, Sn – конечное состояние системы.

Под управлением процессом в целом понимается последовательность шаговых управлений.

Уравнение состояния системы:

Sk = φk (Sk-1; xk).

Sk-1 – предшествующее состояние системы

xk – шаговое управление на k-шаге

φk – некоторая функция.

Целевая функция:

fk – некоторая функция, определяющая критерий эффективности k-шага.

Z – «выигрыш».

Постановка задачи: определить такое допустимое управление x, переводящее систему S из состояния S0 в состояние Sn, при котором целевая функция Z принимает наибольшее/ наименьшее значение.

Принцип Беллмана - вычислительная схема:

Какого бы ни было состояние системы, в результате к.-либо числа шагов, на ближайшем шаге управление надо выбирать так, чтобы оптимальной была сумма выигрышей на всех оставшихся до конца процесса шагах, включая выигрыш на данном шаге.

2 этапа:

1. Этап условной оптимизации (предварительный):

2. Этап безусловной оптимизации:

В основе решения задач динамического программирования лежит принцип оптимальности Беллмана: на каждом этапе принимается такое решение, которое обеспечивает оптимальность с данного этапа до конца процесса, то есть на каждом этапе необходимо принимать решение, просматривая его последствия до самого конца процесса. Так как последовательность решений следует просматривать до самого конца процесса, то варианты анализируют с конца процесса.

Функциональные уравнения Беллмана – это математическая формулировка принципа оптимальности Беллмана. Оптимальное управление обладает следующим свойством: каковы бы ни были начальное состояние S₀ и решение в начальный момент времени, последующие решения должны составлять оптимальное управление относительно состояния, полученного в результате предыдущего решения.

35. Схема решения задачи о распределении средств методом динамического программирования.

Оптимальное распределение ресурсов

Пусть имеется некоторое количество ресурсов х, которое необходимо распределить между п различными предприяти­ями, объектами, работами и т.д. так, чтобы получить мак­симальную суммарную эффективность от выбранного способа распределения.

Сумма прибыли от k-ого предприятия = общая прибыль. Прибыль не зависит от вложения в другие предприятия.

1. Число шагов = число предприятий.

2. Все средства должны быть распределены.

3. На каждом шаге системы (Sk) определяется количество средств, которые остаются после k-ого шага.

4. Выигрышем на k-ом шаге является прибыль, которую приносит k-ое предприятие при Xk.

5. Определяем функциональное уравнение на последнем шаге (сколько средств осталось)

6. Составляем уравнение Беллмана:

36. Классификация задач нелинейного программирования. Задачи на безусловный экстремум.

Задачи нелинейного программировая:

1. Общая задача нелинейного программирования.

2. Задача выпуклого программирования – задачи min-ции выпуклой вниз гладкой функции/ max-ции выпуклой вверх гладкой функции при ограничениях, заданных нелинейными/ линейными неравенствами, определяющими выпуклое множество.

1) Общая задача выпуклого программирования – целевая функция выпуклая и система ограничений также состоит из выпуклой функции.

2) Специальная задача – выпуклая целевая функция и линейная система ограничений.

3) Задача квадратического программирования – квадратическая целевая функция и линейная система ограничений.

3. Динамическое программирование – задачи, у которых целевая функция обладает свойством аддитивности (т.е. когда она представлена в виде суммы слагаемых функции, зависящих от ограниченного числа переменных/ зависящих только от одной переменной).

Z = f1(x1) + f2(x2) + … + fn(xn)

Оптимизация — это выбор наилучшего варианта из множества возможных. Если критерий выбора известен и вариантов не много, то решение может быть найдено простым перебором и сравнением всех ва­риантов. Однако часто бывает так, что количество возможных вариантов велико и перебор практически невозможен. Тогда приходится формализовать задачу, составлять ее математическую модель и применять специальные методы поиска наилучшего решения.

Среди множества оптимизационных задач выделяют группу классических задач оптимизации или задач на безусловный экстремум. Общая постановка этих задач такова: найти вектор  , при котором достигается наибольшее или наименьшее значение скалярной непрерывно дифференцируемой функции  :

.

В основе методов решения классических задач оптимизации лежит теория дифференциального исчисления.

Пусть   — действительная дважды непрерывно дифференцируемая функция аргумента  ,  . Требуется найти наибольшее (или наименьшее) значение данной функции и такое значение аргумента  (оптимальное решение), при котором этот экстремум достигается.

Если точка   является точкой экстремума функции, то она является стационарной точкой функции, т.е. частные производные в этой точке равны нулю:

,  .

Таким образом, экстремумы функции следует искать среди ее стационарных точек. Однако, возможно, не каждая стационарная точка является точкой экстремума.

Для решения вопроса о наличии экстремума функции многих переменных в стационарной точке находят значения вторых частных производных в этой точке и из полученных чисел составляют матрицу, называемую матрицей Гессе:

 

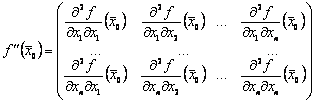
Для того чтобы функция   имела в стационарной точке   локальный минимум, необходимо и достаточно, чтобы в этой точке все главные диагональные миноры матрицы Гессе были положительны.

Для того чтобы функция   имела в стационарной точке   локальный максимум, необходимо и достаточно, чтобы у матрицы Гессе главные диагональные миноры нечетных степеней были отрицательны в этой точке, а миноры четных степеней — положительны.