38. Двойной интеграл в полярных координатах
Пусть область D записывается системой неравенств в полярных координатах:
Такая область называется правильной в полярной системе координат, если каждый луч, выходящий из полюса, пересекает границу области не более, чем в 2-x точках.
По определению
.
Т. к. значение двойного интеграла не зависит от способа разбиения области D на элементарные части, то сделаем это разбиение координатными линиями полярной системы координат (лучами из полюса и концентрическими окружностями).
Переведенный в
полярные координаты двойной интеграл
сведен к повторному по имеющейся записи
области D неравенствами для переменных
и
.
В результате получаем формулу для
вычисления двойного интеграла в полярных
координатах:
.
Обратите внимание,
что в правой части формулы присутствует
множитель
-
это якобиан (определитель Якоби)
преобразования, который находится
следующим образом:
37. Вычисление двойного интеграла путем сведения его к повторному.
Рассмотрим область
D, ограниченную линиями
x
= a, x = b ( a < b ), где φ1(х) и φ2(х) непрерывны
на [a, b]. Тогда любая прямая, параллельная
координатной оси Оу и проходящая через
внутреннюю точку области D, пересекает
границу области в двух точках: N1 и N2
(рис.1). Назовем такую область правильной
в на-
у правлении оси Оу. Аналогично определя-
y=φ2(x) ется область, правильная в направлении
N2 оси Ох. Область, правильную в направле-
нии обеих координатных осей, будем на-
D зывать просто правильной. Например,
правильная область изображена на рис.1.
Пусть функция f(x, y) непрерывна в области D. Рассмотрим выражение
,
(8.1)
называемое двукратным интегралом от функции f(x, y) по области D. Вычислим вначале внутренний интеграл (стоящий в скобках) по переменной у, считая х постоянным. В результате получится непрерывная функция от х:
Полученную функцию
проинтегрируем по х в пределах от а до
b. В результате получим число
Докажем важное свойство двукратного интеграла.
Теорема 8.1. Если область D, правильная в направлении Оу, разбита на две области D1 и D2 прямой, параллельной оси Оу или оси Ох, то двукратный интеграл по области D будет равен сумме таких же интегралов по областям D1 и D2:
.
(8.2)
Доказательство.
а) Пусть прямая х = с разбивает D на D1 и D2 , правильные в направлении Оу. Тогда
+
+
б) Пусть прямая y = h разбивает D на правильные в направлении Оу области D1 и D2 (рис.2). Обозначим через M1 (a1, h) и M2 (b1, h) точки пересечения прямой y = h с гра-ницей L области D.
y Область D1 ограничена непрерывными линиями
y=φ2(x) 1) y = φ1(x);
D2 2) кривой А1М1М2В, уравнение которой запишем
h M1 M2 y = φ1*(x), где φ1*(х) = φ2(х) при а ≤ х ≤ а1 и
A1 D1 B b1 ≤ x ≤ b, φ1*(х) = h при а1 ≤ х ≤ b1;
3) прямыми x = a, x = b.
Область D2 ограничена линиями y = φ1*(x),
A у = φ2(х), а1 ≤ х ≤ b1.
y=φ1(x) Применим к внутреннему интегралу теорему о
разбиении промежутка интегрирования:
O a a1 b1 b
Рис.2.
+
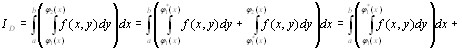
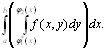
Представим второй из полученных интегралов в виде суммы:
+
+
.
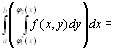
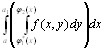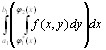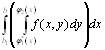Поскольку φ1*(х) = φ2(х) при а ≤ х ≤ а1 и b1 ≤ x ≤ b, первый и третий из полученных интегралов тождественно равны нулю. Следовательно,
ID
=
,
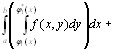то есть
.
Следствие. Таким же образом можно разбить область D на любое число правильных областей. При этом двукратный интеграл по области D будет равен сумме интегралов по частичным областям.
Замечание 1. Используя теорему 8.1 и теоремы о среднем для определенного интеграла, можно доказать, что для двукратного интеграла справедливы соотношения:
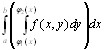
(8.3)
где т и М – соответственно наименьшее и наибольшее значение функции f(x, y) в области D, а S – площадь этой области, и
ID = f(P)S, (8.4)
где Р – точка, принадлежащая области D .
Замечание 2. Более употребительной формой записи двукратного интеграла является
=
(8.5)
Теорема 8.2. Двойной интеграл от непрерывной функции f(x, y) по правильной области D равен двукратному интегралу от этой функции по данной области, то есть
.
(8.6)
Доказательство.
Разобьем область D прямыми, параллельными координатным осям, на п правильных (в основном прямоугольных) областей ΔS1, ΔS2,…, ΔSn. Тогда по теореме 8.1
.
Из (8.4) получим:
,
где справа стоит интегральная сумма,
предел которой равен двойному интегралу
от f по области D, а слева – постоянное
число ID . Переходя к пределу при
,
получим равенство (8.6).
36. Свойства двойных интегралов
1°. Аддитивность. Если функция f(x, y) интегрируема в области D и если область D при помощи кривой Г площади нуль разбивается на две связные и не имеющие общих внутренних точек области D1 и D2, то функция f(x, y) интегрируема в каждой из областей D1 и D2, причем
2°. Линейное свойство. Если функции f(x, y) и g(x, y) интегрируемы в области D, а α и β - любые вещественные числа, то функция [α · f(x, y) + β · g(x, y)] также интегрируема в области D, причем
3°. Если функции f(x, y) и g(x, y) интегрируемы в области D, то и произведение этих функций интегрируемо в D.
4°. Если функции f(x, y) и g(x, y) обе интегрируемы в области D и всюду в этой области f(x, y) ≤ g(x, y), то
5°. Если функция f(x, y) интегрируема в области D, то и функция |f(x, y)| интегрируема в области D, причем
(Конечно, из интегрируемости |f(x, y)| в D не вытекает интегрируемость f(x, y) в D.)
6°. Теорема о среднем значении. Если обе функции f(x, y) и g(x, y) интегрируемы в области D, функция g(x, y) неотрицательна (неположительна) всюду в этой области, M и m - точная верхняя и точная нижняя грани функции f(x, y) в области D, то найдется число μ, удовлетворяющее неравенству m ≤ μ ≤ M и такое, что справедлива формула
(11)
В частности, если функция f(x, y) непрерывна в D, а область D связна, то в этой области найдется такая точка (ξ, η), что μ = f(ξ, η), и формула (11) принимает вид
7°.
Важное геометрическое свойство.
равен
площади области D (Это свойство, как
уже отмечалось ранее, непосредственно
вытекает из определения интегрируемости,
данного в пункте Определение
и существование двойного интеграла для
произвольной области)
31. Пример разложения функции в ряд Фурье.
Теперь разложим в ряд Фурье ту же функцию
,
но при
.
Разложение четной функции надо произвести по несимметричному промежутку, поэтому в отличие от предыдущего примера оно будет полным:
.
При этом коэффициенты Фурье вычисляются
интегрированием по отрезку
,
но т.к. значения функции
в концах отрезка не совпадают, то сумма
ряда Фурье
равна исходной функции лишь в интервале
.
.
.
.
Итак,
для
.
Ответ:
