- •Признак сходимости д’Аламбера в предельной форме
- •Замечание. Если , то признак д′Аламбера не даёт ответа на вопрос о сходимости ряда. Примеры
- •Определение
- •13. Степенные ряды. Теорема Абеля. Область сходимости степенного ряда.
- •14. Свойства степенных рядов. Непрерывность суммы, почленное
- •15. Единственность коэффициентов разложения функции в степенной ряд. Ряд
- •16. Разложение некоторых элементарных функций в ряд Маклорена.
- •17. Область сходимости степенного ряда общего вида. Ряд Тейлора.
- •18. Применение степенных рядов (вычисление значений функций, вычисление
- •Дифференциальное уравнение Бернулли
- •Метод решения Первый способ
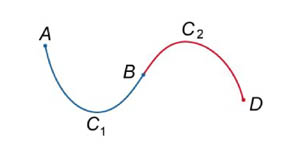
- •49.Формула Грина. Условие независимости криволинейного интеграла второго рода от вида пути
- •48. Вычисления криволинейного интеграла 2-го рода.
- •47.Криволинейный интнграл 2 рода.Его определение,основные свойства и физический смысл.
- •Свойства криволинейного интеграла II рода
- •45. Криволинейный интеграл первого рода
- •42.Вычисление 3 интеграла в сферических координатах.
- •38. Двойной интеграл в полярных координатах
45. Криволинейный интеграл первого рода
![]()
Иллюстрация криволинейного интеграла первого рода на скалярном поле
Свойства
Линейность:
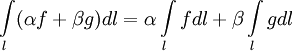
Аддитивность: если
 в
одной точке, то
в
одной точке, то
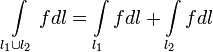
Монотонность: если
 на
на
 ,
то
,
то
![]()
Теорема о среднем для непрерывной вдоль функции :
![]()
Очевидно, что:
![]() .
.
5. Изменение
направления обхода кривой интегрирования
не влияет на знак интеграла:
![]() .
.
6. Криволинейный интеграл первого рода не зависит от параметризации кривой.
44. Криволинейный интеграл первого рода, его определение, геометрический и физический смысл
Определение
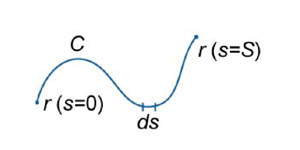
Пусть кривая C
описывается векторной функцией
![]() ,
где переменная s
представляет собой длину
дуги кривой
(рисунок 1). Если на кривой C
определена скалярная
функция F,
то интеграл
,
где переменная s
представляет собой длину
дуги кривой
(рисунок 1). Если на кривой C
определена скалярная
функция F,
то интеграл
 называется
криволинейным
интегралом первого рода
от скалярной функции F
вдоль кривой C
и обозначается как
называется
криволинейным
интегралом первого рода
от скалярной функции F
вдоль кривой C
и обозначается как
![]() Криволинейный
интеграл
Криволинейный
интеграл
![]() существует,
если функция F
непрерывна на кривой C.
существует,
если функция F
непрерывна на кривой C.
|
|
|
Рис.1 |
|
Рис.2 |
42.Вычисление 3 интеграла в сферических координатах.
Тройной интеграл в сферических координатах
Если область V ограничена сферой или частью сферы, тройной интеграл вычислить проще переходом к сферическим координатам. Точка М в сферических координатах однозначно определяются величинами ρ, φ, θ. Здесь ρ- расстояние ОМ до точки из начала координат; φ- угол между проекцией ОМ на плоскость хОу и
осью Ох; θ - угол между положительным направлением оси Oz и лучом ОМ. Связь между прямоугольными декартовыми координатами х, у, z точки М и её
сферическими координатами ρ, φ, θ определяется соотношениями
![]()
где
![]()
Дифференциал объёма в сферических координатах выражается как
![]()
Формула замены переменных в тройном интеграле имеет вид:
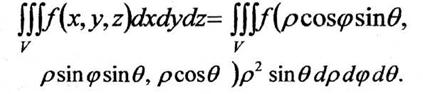
41. Замена переменных в тройном интеграле
Для тройного интеграла имеет место следующее правило замены переменных.
Если функция
![]() непрерывна
в замкнутой области V, а функции
непрерывна
в замкнутой области V, а функции
![]()
![]()
![]() (1)
(1)
имеют непрерывные частные производные в замкнутой области Т пространства UVW и взаимно однозначно отображают эту область на область V пространства XYZ, то имеет место следующая формула:
![]()
![]() (2)
(2)
где
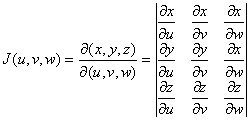 -
якобиан отображения (1).
-
якобиан отображения (1).
Подобно тому как в случае двух переменных модуль якобиана отображения равнялся коэффициенту изменения бесконечно малой площади, модуль якобиана отображения (1) равен коэффициенту изменения бесконечно малого объема при отображении (1).
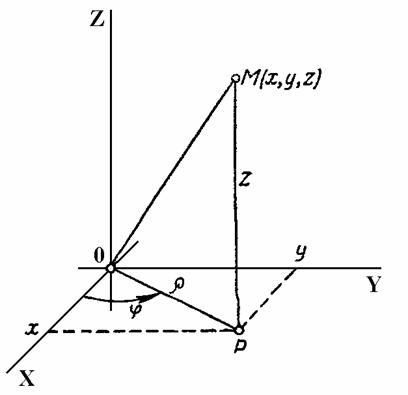
Рис. 4.16.1
Примечание. Формула (2) остается справедливой также и в том случае, если отображение области T на область V взаимно однозначно лишь для внутренних точек этих областей.
Остановимся подробнее на двух наиболее употребительных случаях замены переменных в тройных интегралах.
1. Переход в
тройном интеграле к цилиндрическим
координатам.
Положение точки
![]() пространства
XYZ
однозначно определяется заданием трех
чисел
пространства
XYZ
однозначно определяется заданием трех
чисел
![]() где
где
![]() -
длина радиуса-вектора проекции точки
М на плоскость XOY,
-
длина радиуса-вектора проекции точки
М на плоскость XOY,
![]() -
угол, составляемый этим радиусом-вектором
с осью OX,
z – аппликата точки М. Они связаны с
декартовыми координатами точки М
соотношениями:
-
угол, составляемый этим радиусом-вектором
с осью OX,
z – аппликата точки М. Они связаны с
декартовыми координатами точки М
соотношениями:
![]()
![]()
![]()
По определению
![]() Значение
угла
будем
брать в пределах
Значение
угла
будем
брать в пределах
![]() .
.
На формулы (3), где
переменные
![]() изменяются
в указанных пределах, можно смотреть
как на задание отображения полосы
изменяются
в указанных пределах, можно смотреть
как на задание отображения полосы
![]() пространства
с прямоугольной системой координат
пространства
с прямоугольной системой координат
![]() (рис 4.16.2.) на все пространство XYZ.
Отображение (3) взаимно однозначно всюду,
кроме границы этой полосы.
(рис 4.16.2.) на все пространство XYZ.
Отображение (3) взаимно однозначно всюду,
кроме границы этой полосы.
При этом отображение
(3) плоскости
![]() пространства
соответствует
в пространстве XYZ
цилиндрическая поверхность
пространства
соответствует
в пространстве XYZ
цилиндрическая поверхность
![]() плоскости
плоскости
![]() и
и
![]() пространства
отображаются
в пространстве XYZ
соответственно в полуплоскость,
проходящую через ось OZ
под углом
пространства
отображаются
в пространстве XYZ
соответственно в полуплоскость,
проходящую через ось OZ
под углом
![]() к
оси OX
и плоскость
(рис.2.15.3.).
Якобиан отображения:
к
оси OX
и плоскость
(рис.2.15.3.).
Якобиан отображения:

неотрицателен в
данной полосе (![]() только на границе полосы).
только на границе полосы).
Рис. 4.16.2
Применяя формулу замены переменных в тройном интеграле к отображению (3), получим так называемую формулу перехода в тройном интеграле от декартовых координат к цилиндрическим координатам:
![]()
Здесь Т – область пространства , образом которой при отображении (3) является область V.
Пример.
Вычислить объем тела V, ограниченного
поверхностями ![]() в
цилиндрических координатах.
в
цилиндрических координатах.
Обозначим через
Т область пространства
,
ограниченную поверхностями
![]() (рис.4.16.4.). При отображении (3) ее образом
в пространстве XYZ
будет данная область V. Поэтому
(рис.4.16.4.). При отображении (3) ее образом
в пространстве XYZ
будет данная область V. Поэтому
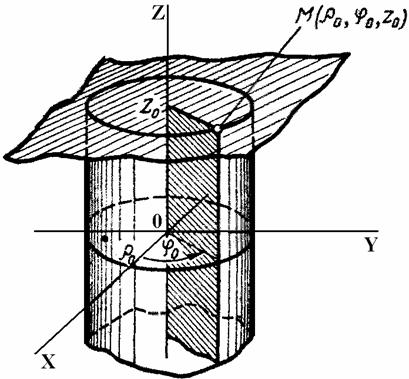
Рис. 4.16.3

Примечание. Расстановку пределов при вычислении тройного интеграла в цилиндрических координатах можно производить, используя чертеж области V в пространстве XYZ и геометрический смысл цилиндрических координат.
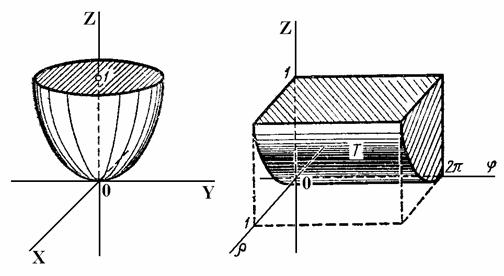
Рис. 4.16.4
Так, например, при
расстановке пределов в полученном выше
интеграле можно было рассуждать следующим
образом. Так как область V на плоскость
XOY
проектируется в круг
![]() то
цилиндрическая координата
точек
тела изменяется в пределах от 0 до
то
цилиндрическая координата
точек
тела изменяется в пределах от 0 до
![]() .
В сечении тела полуплоскостью
.
В сечении тела полуплоскостью
![]() ,
получаем криволинейный треугольник
(см. заштрихованную область на рис.2.15.5.).
Для его точек цилиндрическая координата
изменяется в пределах от
до
,
получаем криволинейный треугольник
(см. заштрихованную область на рис.2.15.5.).
Для его точек цилиндрическая координата
изменяется в пределах от
до
![]() Постоянному
значению
,
Постоянному
значению
, ![]() в
пространстве XYZ
соответствует цилиндр
в
пространстве XYZ
соответствует цилиндр
![]() В пересечении этого цилиндра с
заштрихованной в полуплоскости
областью
получаем отрезок прямой, вдоль которой
переменная z изменяется от значения z
для точки, лежащей на параболоиде, до
значения z = 1 (для точки, лежащей на
плоскости z=1).
В пересечении этого цилиндра с
заштрихованной в полуплоскости
областью
получаем отрезок прямой, вдоль которой
переменная z изменяется от значения z
для точки, лежащей на параболоиде, до
значения z = 1 (для точки, лежащей на
плоскости z=1).
Выражая эти
значения в цилиндрических координатах
(![]() ,
окончательно получаем:
,
окончательно получаем:
Уже в студенческие годы Ньютон зарекомендовал себя пытливым, упорным и настойчивым исследователем. Так, будучи студентом, Ньютон доказал теорему о биноме. С тех пор формула бинома стала называться «биномом Ньютона». Студентом же он вплотную подошел к проблеме всемирного тяготения. Позднее этой проблеме он посвятил целый трактат «Принципы натуральной философии
40.
39.