49.Формула Грина. Условие независимости криволинейного интеграла второго рода от вида пути

Интегрирования

Пусть D - некоторая замкнутая область на плоскости хОу, ограниченная контуром L. На ней заданы функции Р = Р(х,у) и Q = Q(x,y), непрерывные на D вместе со своими частными производными первого порядка. Формула Грина связывает криволинейный интеграл второго рода по L с двойным интегралом по области D:

Движение по контуру L - в положительном направлении.

С помощью формулы Грина значение криволинейного интеграла по замкнутому контуру можно найти, вычислив двойной интеграл.

48. Вычисления криволинейного интеграла 2-го рода.

 

Теорема . Пусть кривая L задана параметрическими уравнениями

                         x = φ(t), y = ψ(t), z = χ(t),     α ≤ t ≤ β ,

где φ, ψ, χ – непрерывно дифференцируемые функции, и на ней задана непрерывная функция f(x, y, z). Тогда интеграл (10.5) существует и имеет место равенство

                        .                           (10.8)

Доказательство.

Запишем Δxi = xi – xi-1 = φ(ti) – φ(ti-1) и преобразуем последнюю разность по формуле Лагранжа:   φ(ti) – φ(ti-1) = φ΄(τi)Δti, где τi – некоторое значение t, заключенное между ti-1 и ti. Выберем точку Мi так, чтобы ее координаты соответствовали значению параметра, равному τi : Mi(φ(τi), ψ(τi), χ(τi)). Подставив эти значения в формулу (10.5), получим:          

                         .

Справа получен предел интегральной суммы для функции f(φ(t),ψ(t),χ(t))φ΄(t) на отрезке [α, β], равный определенному интегралу от этой функции:

                         ,

что и требовалось доказать.

 

Следствие. Аналогичные соотношения можно получить для криволинейных интегра-лов вида , откуда следует, что

 

           

47.Криволинейный интнграл 2 рода.Его определение,основные свойства и физический смысл.

Криволинейным интегралом II рода от функций и по плоской кривой от точки к точке называют предел ,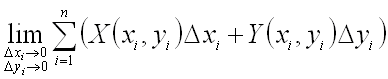 где точки – точки, которые разбивают участок кривой от точки до точки на частей, а и – приращения соответствующих координат при переходе от точки к точке . Криволинейный интеграл II рода обозначают: 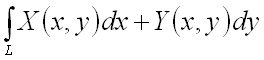или 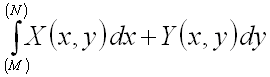. Направление по кривой от точки до точки называется направлением интегрирования. Если кривая пространственная, то криволинейный интеграл II рода от трех функций , , определяется аналогично:

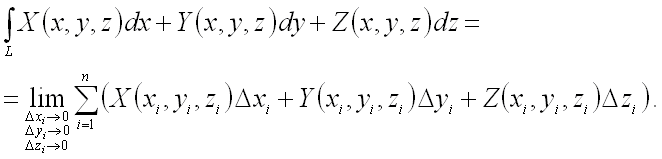
Свойства криволинейного интеграла II рода

1. Криволинейный интеграл определяется подынтегральным выражением, формой кривой интегрирования и указанием направления интегрирования. При изменении направления интегрирования криволинейный интеграл меняет знак. 2. Если участок кривой от точки до точки разбить точкой на две части и , то непосредственно из определения криволинейного интеграла II рода следует, что .

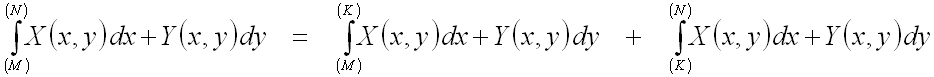Если криволинейный интеграл II рода вычисляется по замкнутой кривой , то его называют криволинейным интегралом II рода по замкнутому контуру и обозначают 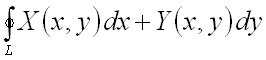. При вычислении криволинейного интеграла II рода по замкнутому контуру необходимо учитывать направление обхода замкнутой кривой (против часовой стрелки или по часовой стрелке).

46. Вычисление криволинейного интеграла первого рода в декартовой и

полярной системах координат.