14. Свойства степенных рядов. Непрерывность суммы, почленное

интегрирование и дифференцирование степенных рядов.

Свойства степенных рядов:

1) Сумма степенного ряда является непрерывной функцией в интервале сходимости.

2)Степенные ряды   и   имеют один и тот же радиус сходимости.

3)Степенные ряды можно почленно дифференцировать в интервале сходимости любое число раз и для S(x).

4)Степенной ряд можно почленно интегрировать по любому промежутку, принадлежащему интервалу сходимости.

Непрерывность суммы

На любом отрезке  целиком лежащем внутри интервала сходимости степенного ряда (1.2), сумма ряда есть непрерывная функция.

Доказательство. Каждая частичная сумма степенного ряда, очевидно, является непрерывной функцией. По теореме 2.1 на любом отрезке целиком лежащем внутри интервала сходимости ряда сходимость является равномерной. Сумма ряда, являющаяся пределом равномерно сходящейся последовательности непрерывных функций, сама является непрерывной функцией. Теорема доказана.

Дифференцирование и интегрирование степенных рядов

Рассмотрим степенной ряд  , имеющий радиус сходимости R > 0: Функция   является непрерывной функцией при |x| < R. Степенной ряд внутри интервала сходимости можно дифференцировать почленно. При этом производная степенного ряда выражается формулой Степенной ряд можно также почленно интегрировать на отрезке, который расположен внутри интервала сходимости. Следовательно, если − R < b < x < R, то выполняется равенство Если ряд интегрируется на отрезке [0; x], то справедлива формула:

15. Единственность коэффициентов разложения функции в степенной ряд. Ряд

Маклорена.

Определение

Пусть функция   бесконечно дифференцируема в некоторойокрестности точки  . Формальный ряд

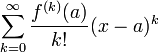
называется рядом Тейлора функции   в точке  .

Связанные определения

• В случае, если 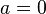 , этот ряд также называется рядом Макло́рена.

Свойства

• Если   есть аналитическая функция в любой точке a, то её ряд Тейлора в любой точке   области определения   сходится к   в некоторой окрестности  .

• Существуют бесконечно дифференцируемые функции, ряд Тейлора которых сходится, но при этом отличается от функции в любой окрестности  . Например, Коши предложил такой пример:

У этой функции все производные в нуле равны нулю, поэтому коэффициенты ряда Тейлора в точке   равны нулю.

16. Разложение некоторых элементарных функций в ряд Маклорена.

Разложение функции f(x)=e^x в ряд Маклорена.

f(x)=f′(x)=f″(x)=…=f⁽ⁿ⁾(x)=…=e^x.

f(0)=f′(0)=f″(0)=…=f⁽ⁿ⁾(0)=…=1.

Составим для функции f(x)=e^x формально ряд Маклорена: 1+  .

Найдём области сходимости этого ряда.

 при любых x, следовательно, областью сходимости ряда является промежуток  (-∞;+∞). Заметим, что так как ряд сходится абсолютно, то    при любых х и тем более   при любых х. Так как f⁽ⁿ⁺¹⁾(x)=e^x и f⁽ⁿ⁺¹⁾(с)=e^с, то  =e^c =0. Таким образом, имеет место разложение при x (-∞;+∞)

e^x=1+  .     (32)

17. Область сходимости степенного ряда общего вида. Ряд Тейлора.

Аналитические функции. Пример функции, не являющейся аналитической.