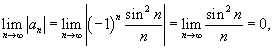- •Признак сходимости д’Аламбера в предельной форме
- •Замечание. Если , то признак д′Аламбера не даёт ответа на вопрос о сходимости ряда. Примеры
- •Определение
- •13. Степенные ряды. Теорема Абеля. Область сходимости степенного ряда.
- •14. Свойства степенных рядов. Непрерывность суммы, почленное
- •15. Единственность коэффициентов разложения функции в степенной ряд. Ряд
- •16. Разложение некоторых элементарных функций в ряд Маклорена.
- •17. Область сходимости степенного ряда общего вида. Ряд Тейлора.
- •18. Применение степенных рядов (вычисление значений функций, вычисление
- •Дифференциальное уравнение Бернулли
- •Метод решения Первый способ
- •49.Формула Грина. Условие независимости криволинейного интеграла второго рода от вида пути
- •48. Вычисления криволинейного интеграла 2-го рода.
- •47.Криволинейный интнграл 2 рода.Его определение,основные свойства и физический смысл.
- •Свойства криволинейного интеграла II рода
- •45. Криволинейный интеграл первого рода
- •42.Вычисление 3 интеграла в сферических координатах.
- •38. Двойной интеграл в полярных координатах
Числовой ряд. Сумма ряда, его сходимость. Геометрическая прогрессия и гармонический ряд.
Числовой ряд — это числовая последовательность, рассматриваемая вместе с другой последовательностью, которая называется последовательностью частичных сумм (ряда).
Рассматриваются числовые ряды двух видов
вещественные числовые ряды — изучаются в математическом анализе;
комплексные числовые ряды — изучаются в комплексном анализе;
Важнейший вопрос исследования числовых рядов — это сходимость числовых рядов.
В соответствии с этим говорится о сходимости числового ряда:
числовой ряд сходится, если сходится последовательность его частичных сумм;
числовой ряд расходится, если расходится последовательность его частичных сумм:
числовой ряд сходится абсолютно, если сходится ряд из модулей его членов.
Сумма
числового ряда ![]() определяется
как предел, к которому стремятся суммы
первых n слагаемых ряда,
когда n неограниченно
растёт. Если такой предел существует и
конечен, то говорят, что ряд сходится,
в противном случае — что он
расходится[1].
Элементы ряда
определяется
как предел, к которому стремятся суммы
первых n слагаемых ряда,
когда n неограниченно
растёт. Если такой предел существует и
конечен, то говорят, что ряд сходится,
в противном случае — что он
расходится[1].
Элементы ряда ![]() представляют
собой комплексные
числа (в
частности, вещественные).
представляют
собой комплексные
числа (в
частности, вещественные).
Геометри́ческая
прогре́ссия —
последовательность чисел ![]() (членов прогрессии),
в которой каждое последующее число,
начиная со второго, получается из
предыдущего умножением его на определённое
число
(членов прогрессии),
в которой каждое последующее число,
начиная со второго, получается из
предыдущего умножением его на определённое
число ![]() (знаменатель прогрессии),
где
(знаменатель прогрессии),
где ![]() ,
, ![]() :
: ![]() .
.
В математике гармонический ряд представляет собой сумму, составленную из бесконечного количества членов, обратных последовательным числам натурального ряда[1]:
 .
.
Ряд назван гармоническим,
так как складывается из «гармоник»: ![]() -я
гармоника, извлекаемая из скрипичной
струны, — это основной тон, производимый
струной длиной
-я
гармоника, извлекаемая из скрипичной
струны, — это основной тон, производимый
струной длиной ![]() от
длины исходной струны
от
длины исходной струны
Свойства сходящихся рядов. Остаток ряда. Необходимое условие сходимости.
1°. Отбрасывание конечного числа членов не влияет на сходимость ч.р.
Рассмотрим![]() и
и![]() Пусть
Пусть![]()
![]() тогда
тогда
![]() (29.1)
(29.1)
Если
существует конечный предел справа в
(29.1), то существует и предел слева, и
ряд![]() сходится
сходится
2°.
Если ряд![]() сходится
и имеет сумму S, то ряд
сходится
и имеет сумму S, то ряд![]()
с = const, сходится и имеет сумму cS.
Пусть![]() тогда
тогда
![]()
3°.
Если ряды![]() сходятся
и имеют суммы
сходятся
и имеют суммы ![]() соответственно,
то ряд
соответственно,
то ряд![]() сходится
и имеет сумму
сходится
и имеет сумму![]()
Пусть![]()
![]() тогда
тогда
![]()
Остаток ряда
Ряд, полученный отбрасыванием от исходного n первых членов, называется n-м остатком ряда.
Обозначение:

Все члены, кроме тех, что входят в n-й остаток ряда, в сумме дают т. н. n-ю частичную сумму ряда.
Для сходимости
ряда |
Доказательство
По условию последовательность ![]() ,
а следовательно, и её остаток
,
а следовательно, и её остаток ![]() имеют
общий конечный предел
имеют
общий конечный предел ![]() ,
но
,
но ![]() и
поэтому
и
поэтому ![]() ,
что равносильно бесконечной малости
,
что равносильно бесконечной малости
Знакопостоянные ряды. Первый признак сравнения.
Определение. Ряды,
все члены которых имеют одинаковые
знаки, называются знакопостоянными.
Для определенности, если это не будет
оговорено особо, мы будем рассматривать
ряды с положительными членами или
знакоположительные ряды: P, Q,
…: pn>0, qn>0 , …
для ![]()
Очевидно, что последовательность частичных сумм знакоположительных рядов монотонно возрастает: P1<P2< … <Pn<Pn+1< … . Следовательно, верна
Теорема. Для сходимости знакоположительного ряда необходимо и достаточно, чтобы
последовательность его частичных сумм была ограничена.
Если общий член ряда не стремится к нулю, то ряд расходится
Или короче: Если ![]() ,
то ряд расходится.
,
то ряд расходится.
В качестве «динамической»
переменной вместо «икса» у нас выступает ![]() .
Букву можно заменить другой буквой, и
это не страшно, однако есть разница с
содержательной точки зрения. Пределы
с «иксом» называют пределами функций,
а пределы с переменной «эн» называют
пределами числовых последовательностей.
Очевидное отличие состоит в том, что
переменная «эн» принимает дискретные
(прерывные) натуральные значения: 1, 2, 3
и т.д. Но данный факт мало сказывается
на методах решения пределов и способах
раскрытия неопределенностей.
.
Букву можно заменить другой буквой, и
это не страшно, однако есть разница с
содержательной точки зрения. Пределы
с «иксом» называют пределами функций,
а пределы с переменной «эн» называют
пределами числовых последовательностей.
Очевидное отличие состоит в том, что
переменная «эн» принимает дискретные
(прерывные) натуральные значения: 1, 2, 3
и т.д. Но данный факт мало сказывается
на методах решения пределов и способах
раскрытия неопределенностей.
Докажем, что ряд из первого
примера ![]() расходится.
Общий
член ряда:
расходится.
Общий
член ряда: ![]()
![]() Вывод:
ряд
расходится,
так как не выполнен необходимый признак
сходимости ряда.
Вывод:
ряд
расходится,
так как не выполнен необходимый признак
сходимости ряда.
Признаки сравнения рядов
Даны
два ряда ![]() и
и ![]() −
такие, что
−
такие, что ![]() для
всех n.
Тогда справедливы следующие признаки:
для
всех n.
Тогда справедливы следующие признаки:
Если сходится, то также сходится;
Если расходится, то также расходится.
Признак Даламбера
При́знак д’Аламбе́ра (или Признак Даламбера) — признак сходимости числовых рядов, установлен Жаном д’Аламбером в 1768 г.
Если для числового ряда
![]()
существует
такое число
, ![]() ,
что начиная с некоторого номера
выполняется неравенство
,
что начиная с некоторого номера
выполняется неравенство
![]()
то данный ряд абсолютно сходится; если же, начиная с некоторого номера
![]()
то ряд расходится.
Признак сходимости д’Аламбера в предельной форме
Если существует предел
![]()
то
рассматриваемый ряд абсолютно сходится
если ![]() ,
а если
,
а если ![]() —
расходится .
—
расходится .
Замечание. Если , то признак д′Аламбера не даёт ответа на вопрос о сходимости ряда. Примеры
Ряд
![]()
абсолютно сходится для всех
комплексных ![]() ,
так как
,
так как
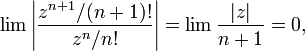
Ряд
![]()
расходится при всех ![]() ,
так как
,
так как
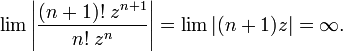
Если , то ряд может как сходиться, так и расходиться: оба ряда
![]() и
и
![]()
удовлетворяют этому условию, причём первый ряд расходится, а второй сходится.
Радикальный признак Коши
Радикальный признак Коши
Радикальный признак Коши — признак сходимости числового ряда:
-
Если для числового ряда
с неотрицательными членами существует такое число
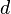 ,
, 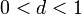 ,
что, начиная с некоторого номера,
выполняется неравенство
,
что, начиная с некоторого номера,
выполняется неравенство 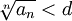 ,
то данный ряд сходится.
,
то данный ряд сходится.
|
Предельная форма
Условие радикального признака равносильно следующему:
![]()
То есть можно сформулировать радикальный признак сходимости знакоположительного ряда в предельной форме:
-
Если для ряда
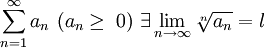 ,
то
,
тоесли
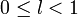 ряд
сходится,
ряд
сходится,если
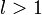 ряд
расходится,
ряд
расходится,если
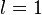 вопрос
о сходимости ряда остается открытым.
вопрос
о сходимости ряда остается открытым.
Доказательство
1.
Пусть ![]() .
Очевидно, что существует такое
.
Очевидно, что существует такое ![]() ,
что
,
что ![]() .
Поскольку существует предел
.
Поскольку существует предел ![]() ,
то подставив в определение предела
выбранное
,
то подставив в определение предела
выбранное ![]() получим:
получим:
![]()
Раскрыв модуль, получаем:
![]()
![]()
![]()
Поскольку
,
то ряд ![]() сходится.
Следовательно, по признаку
сравнения ряд
сходится.
Следовательно, по признаку
сравнения ряд ![]() тоже
сходится.
тоже
сходится.
2.
Пусть
.
Очевидно, что существует такое
,
что ![]() .
Поскольку существует предел
,
то подставив в определение предела
выбранное
получим:
.
Поскольку существует предел
,
то подставив в определение предела
выбранное
получим:
Раскрыв модуль, получаем:
Поскольку
,
то ряд ![]() расходится.
Следовательно, по признаку
сравнения ряд
тоже
расходится.
расходится.
Следовательно, по признаку
сравнения ряд
тоже
расходится.
Примеры
1. Ряд
![]()
сходится, так как выполняется условие предельной формы радикального признака теоремы Коши
![]()
7. Интегральный признак сходимости
Интегральный
признак сходимости. Сходимость ряда ![]()
Теорема. Пусть ![]() - непрерывная, неотрицательная, монотонно
убывающая функция, определенная при
- непрерывная, неотрицательная, монотонно
убывающая функция, определенная при ![]() .
Тогда ряд
.
Тогда ряд ![]() и
интеграл
и
интеграл ![]() либо оба сходятся, либо оба
расходятся. Основные
теоремы о пределах Введение
в математический анализ
либо оба сходятся, либо оба
расходятся. Основные
теоремы о пределах Введение
в математический анализ
Доказательство. Ввиду
монотонности при всех
выполняются
неравенства ![]() .
Интегрируя, получаем
.
Интегрируя, получаем 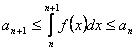 .
Тогда
.
Тогда ![]() ,
или
,
или ![]() .
Поэтому если
сходится,
то
.
Поэтому если
сходится,
то ![]() .
Тогда
.
Тогда ![]()
![]() и
и ![]() ,
, ![]() ряд сходится.
ряд сходится.
Пусть
теперь наоборот, известно, что ряд
сходится. Тогда ![]() .
Взяв произвольное
.
Взяв произвольное ![]() выберем
так,
чтобы
выберем
так,
чтобы ![]() .
Тогда
.
Тогда ![]() .
Значит,
сходится.
.
Значит,
сходится.
8. Знакочередующиеся ряды. Теорема Лейбница. Оценка остатка ряда.
8.Знакочередующиеся ряды. Оценка остатка.
Ряд называется знакочередующимся, если его члены попеременно принимают значения противоположных знаков, т. е.:
![]()
Признак Лейбница
Признак Лейбница — признак сходимости знакочередующегося ряда, установлен Готфридом Лейбницем. Формулировка теоремы:
-
Пусть для знакочередующегося ряда
выполняются следующие условия:
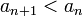 (монотонное
убывание {an})
(монотонное
убывание {an}) .
.
Тогда этот ряд сходится.
Если, выполнены все условия, и ряд из модулей ( ) сходится, то исходный ряд сходится абсолютно. Если выполнены все условия, но ряд из модулей расходится, то исходный ряд сходится условно. Строгая положительность существенна.
Ряды, удовлетворяющие признаку Лейбница, называются рядами Лейбница. Следует отметить, что этот признак является достаточным, но не необходимым.
Пример
![]() .
Ряд из модулей имеет вид
.
Ряд из модулей имеет вид ![]() —
этогармонический
ряд, который
расходится.
—
этогармонический
ряд, который
расходится.
Теперь воспользуемся признаком Лейбница:
знакочередование выполнено
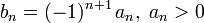
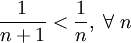
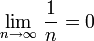 .
.
Следовательно, так как все условия выполнены, но ряд из модулей расходится, искомый ряд сходится условно.
Оценка остатка ряда Лейбница
Из доказательства признака Лейбница следует, что сумма знакопеременного сходящегося ряда меньше по модулю первого члена остатка ряда. Поскольку любой остаток ряда rn является также рядом Лейбница, то для него справедливо:
![]() .
.
Теорема Лейбница (Характер членов слагаемых Лейбница) — теоремаоб условной сходимости знакочередующихся рядов, сформулированная немецким математиком Лейбницем.
Формулировка
Теорема формулируется следующим образом. Знакочередующийся ряд
![]()
сходится, если выполняются оба условия:
Следствие
Из теоремы Лейбница вытекает следствие, позволяющее оценить погрешность вычисления неполной суммы ряда:
![]()
Остаток сходящегося
знакочередующегося ряда ![]() будет
по модулю меньше первого отброшенного
слагаемого:
будет
по модулю меньше первого отброшенного
слагаемого:
![]()
9. Знакопеременные ряды. Абсолютная и условная сходимость.
Числовой ряд, содержащий бесконечное множество положительных и бесконечное множество отрицательных членов, называется знакопеременным. Частным случаем знакопеременного ряда являетсязнакочередующийся ряд, то есть такой ряд, в котором последовательные члены имеют противоположные знаки. Признак Лейбница Для знакочередующихся рядом действует достаточный признак сходимости Лейбница. Пусть {an} является числовой последовательностью, такой, что 1. an+1 < an для
всех n;
2. Тогда знакочередующиеся
ряды Абсолютная и условная сходимость Ряд
называется абсолютно
сходящимся, если ряд |
Пример 1 |
|
Исследовать на сходимость ряд Решение. Применим достаточный признак Лейбница для знакочередующихся рядов. Получаем поскольку
10. Свойства абсолютно и условно сходящихся рядов |
Условно сходящиеся ряды
Свойства
Если ряд условно сходится, то ряды, составленные из его положительных и отрицательных членов, расходятся.
Путём изменения порядка членов условно сходящегося ряда можно получить ряд, сходящийся к любой наперёд заданной сумме или же расходящийся (теорема Римана).
При почленном умножении двух условно сходящихся рядов может получиться расходящийся ряд.
Абсолютно сходящиеся ряды
Свойства
из сходимости интеграла
 вытекает
сходимость интеграла
вытекает
сходимость интеграла 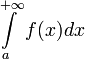 .
.Для выявления абсолютной сходимости несобственного интеграла первого рода используют признаки сходимости несобственных интегралов первого рода от неотрицательных функций.
Если интеграл расходится, то для выявления условной сходимости несобственного интеграла первого рода могут быть использованы признаки Абеля и Дирихле.
11. Признаки сходимости для знакопеременных рядов.
Признак Лейбница
Для знакочередующихся рядом действует достаточный признак сходимости Лейбница. Пусть {an} является числовой последовательностью, такой, что
1. an+1 < an для всех n; 2. .
Тогда знакочередующиеся ряды и сходятся.
Абсолютная и условная сходимость
Ряд называется абсолютно сходящимся, если ряд также сходится. Если ряд сходится абсолютно, то он является сходящимся (в обычном смысле). Обратное утверждение неверно. Ряд называется условно сходящимся, если сам он сходится, а ряд, составленный из модулей его членов, расходится.
12. Функциональные ряды. Поточечная сходимость. Область сходимости.
Обычный числовой ряд, вспоминаем, состоит из чисел:
![]()
Все члены ряда ![]() –
это ЧИСЛА.
–
это ЧИСЛА.
Функциональный же ряд состоит из ФУНКЦИЙ:
![]()
В общий член ряда ![]() помимо
многочленов, факториалов и других
подарков непременновходит
буковка «икс». Выглядит это, например,
так:
помимо
многочленов, факториалов и других
подарков непременновходит
буковка «икс». Выглядит это, например,
так: ![]() .
Как и числовой ряд, любой функциональный
ряд можно расписать в развернутом
виде:
.
Как и числовой ряд, любой функциональный
ряд можно расписать в развернутом
виде:
![]()
Как видите, все члены
функционального ряда ![]() –
это функции.
–
это функции.
Наиболее популярной разновидностью функционального ряда является степенной ряд.
Поточечная сходимость:

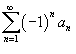 и
и 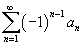 сходятся.
сходятся.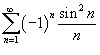 .
.