1.5.3. Соотношение между мощностью падающего и дифрагированного излучения при дифракции света на амплитудной гармонической решетке

Взяв за основу проделанный выше расчет мощности для случая дифракции на щели, рассчитаем распределение мощности излучения по дифракционным порядкам при дифракции оптической волны с амплитудой на амплитудной дифракционной решетке с глубиной модуляции т. Построим диаграммы распределения мощности по порядкам дифракции, положив т = 1. Сравним полную падающую мощность и суммарную мощность излучения в дифракционных порядках. Проанализируем баланс мощности в системе и соотношение мощностей в различных дифракционных порядках.

Решение. Взяв в качестве исходного выражения пространственный спектр амплитудной дифракционной решетки (1.27), вычислим интегралы по переменной  для каждого из дифракционных порядков.

Нулевой порядок:

(1.33)

Первый порядок:

(1.34)

Первый отрицательный порядок:

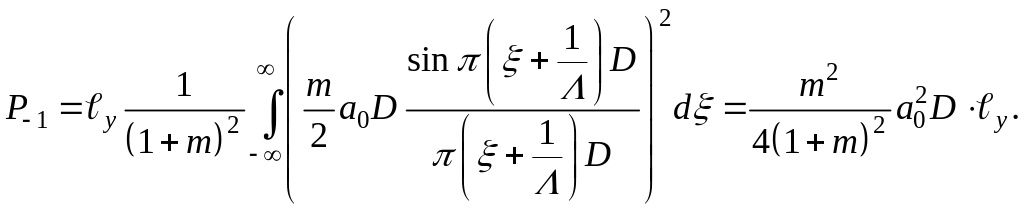(1.35)

Как видно из расчетов, при максимальной глубине модуляции т = 1 суммарная мощность всех порядков дифракционного излучения составляет

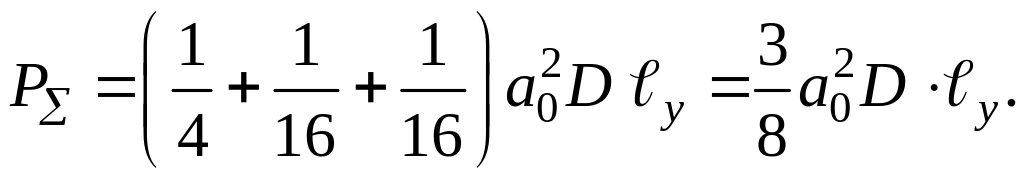
Полная мощность, падающая на дифракционную решетку, равна . Остальная мощность, т.е. , поглощается в амплитудной гармонической решетке. Отражение излучения при расчетах полагалось равным нулю.

Равенство Парсеваля здесь должно выполняться только в пространстве справа от амплитудной решетки. Проверим это. Проинтегрируем по координате х распределение мощности излучения, прошедшего через решетку. Для упрощения вычислений положим, что в апертуре D укладывается целое число периодов решетки, при этом интегралы от функций и равны нулю.

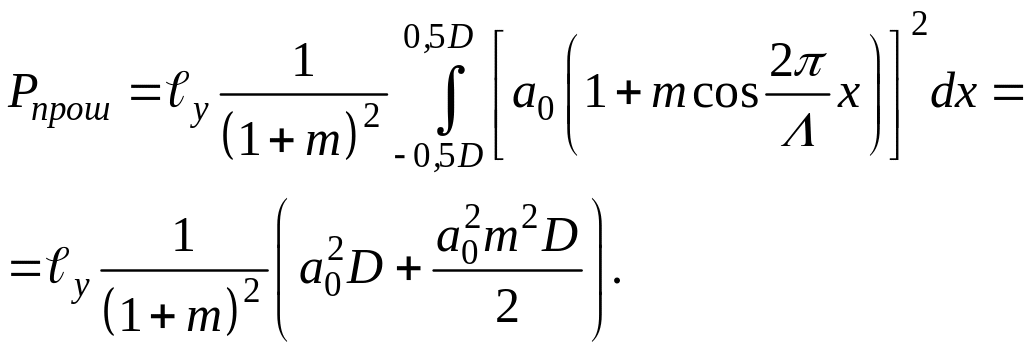
При максимальной глубине модуляции т = 1 имеем:

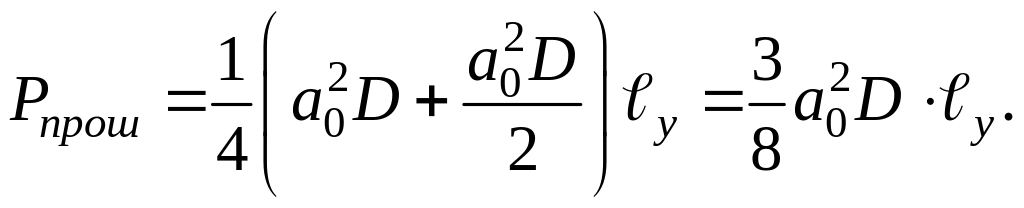(1.36)

Таким образом, мы показали, что прошедшая мощность и суммарная мощность всех компонент пространственного спектра равны, равенство Парсеваля выполняется.

Интересно по результатам этих расчетов оценить эффективность амплитудной дифракционной решетки. Эффективностью дифракционной решетки принято называть отношение мощности оптического пучка в первом дифракционном порядке, к полной падающей мощности дифракционного пучка.

(1.37)

Из (1.34) и (1.31) при т = 1 получим величину  = 1/16 = 6,25%.

Как видно, амплитудная решетка характеризуется довольно низкой эффективностью дифракции.

1.6. Методика наблюдения пространственных спектров дифракции

и измерения их параметров

В оптике измеряют энергетические характеристики излучения: мощность излучения или энергию излучения, падающую на площадку. Измерения можно выполнять с помощью фотодиодов, фотоэлементов, болометров. Если используется фотодиод с обратным смещением р-п перехода, то фототок пропорционален мощности падающего излучения в широком диапазоне интенсивностей светового потока. При измерениях мощности монохроматического светового излучения используют параметр фотодиода, который обычно называют

монохроматической чувствительностью^* . При этом фототок связан с падающей мощностью формулой:

, (1.38)

где Р − падающая мощность; − фототок.

Предельную величину монохроматической чувствительности для заданной длины волны излучения можно оценить, пользуясь следующей простой пропорцией. Допустим, что каждый квант света порождает в фотодетекторе один электрон. Энергия кванта равна , где h  постоянная Планка,  частота световой волны. Заряд электрона равен е. Поток света с интенсивностью п квантов в секунду создает ток величиной п электронов в секунду.

, а это не что иное как соотношение между мощностью излучения и фототоком : .

Таким образом, соотношение между током фотодетектора и световой мощностью при отсутствии потерь электронов в процессе преобразования света в электрический ток (т.е. при 100% квантовой эффективности) составит:

. (1.39)

Проиллюстрируем это соотношение расчетом для  = 0,6328 мкм, т.е. для случая детектирования излучения красного гелий-неонового лазера.

е = 1,6010^-19 Кулон =.1,6010^-19 Асек

h = 6,6210^-34 [Джcек], т.е. (Втсек²).

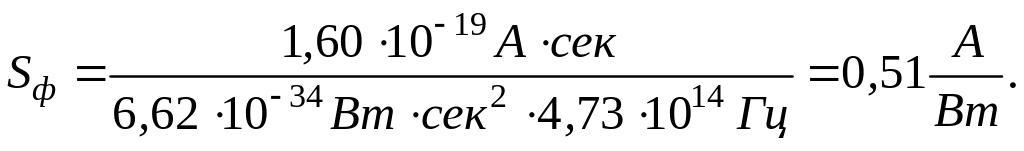
Следует подчеркнуть два обстоятельства:

• Рассчитанная величина 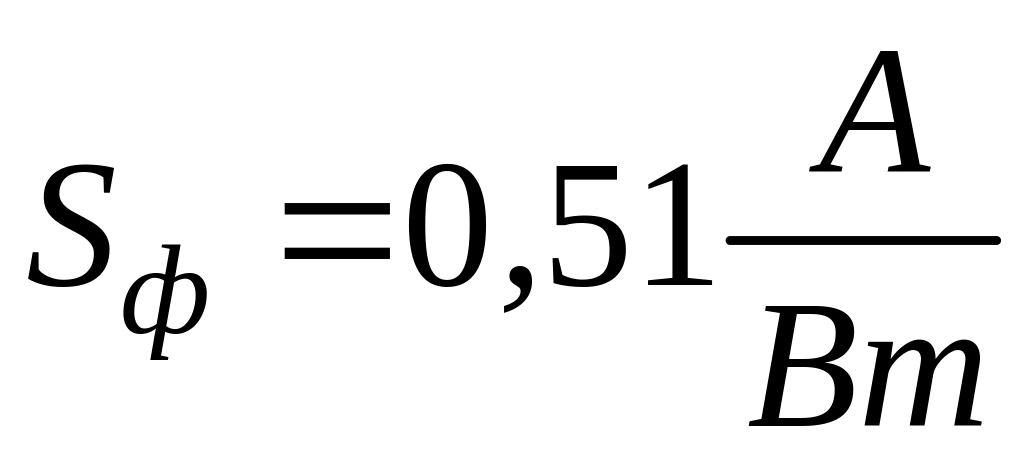является предельной для данной длины волны. Реальная величина у фотодетектора и фотоэлемента несколько меньше, т.к.обычно не удается достигнуть 100% квантовой эффективности. Кроме того, часть световой мощности теряется из-за отражения света.

• Величина зависит от длины волны. При уменьшении длины волны света, т.е. с увеличением частоты величина снижается.

• Соотношение (1.39) справедливо только для тех фотодетекторов, где отсутствует умножение носителей заряда под действием электрического поля.

Визуальное наблюдение и измерение распределения мощности пространственных спектров можно проводить на экране, удаленном от объекта, по следующей схеме, изображенной на рис. 1.6.

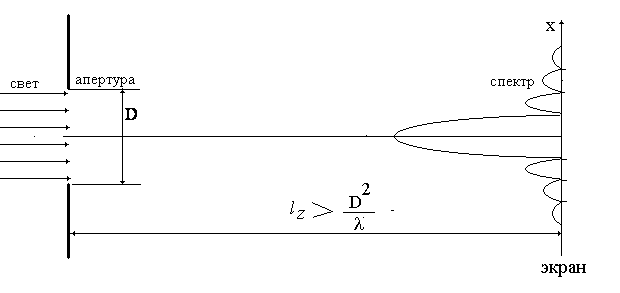
Рис.1.6 . Схема наблюдения пространственного спектра в дальней зоне.

В схеме, изображенной на рис. 1.6, расстояние должно выбираться, исходя из следующего условия. Экран располагается в области дифракции Фраунгофера, т.е. на расстоянии , где D − размер апертуры, а  − длина световой волны. При размере апертуры порядка 1 мм и длине волны 0,63 мкм это расстояние составит = 1/0,6310^-3=1,610³ мм. При увеличении размера апертуры D наблюдение пространственного спектра по этой методике требует очень больших расстояний, так как требуемое возрастает пропорционально квадрату линейного размера апертуры, поэтому подобная схема может применяться только при небольших линейных размерах апертуры и при небольшом отношении .

Пример. Пусть в плоскости П₁ расположена одномерная амплитудная дифракционная решетка с периодом = 0,1 мм в направлении оси 0х. Апертура имеет форму щели размером d =1 мм по координате 0х с центром в точке

х = 0. Слева на апертуру падает плоская волна с длиной волны  = 0,63 мкм, направленная вдоль оси 0z.

В плоскости наблюдения х₂у₂ на расстоянии = 10 метров от плоскости х₁у₁ расположен экран. Как было показано ранее, в спектре пространственных частот можно выделить три главных максимума на пространственных частотах , , .

Этим пространственным частотам соответствуют углы дифракции:

и .

Так как отношение , можно использовать приближение , и записать

,

т.е. (₁ = 6,310^-3 радиан, _-1 = -6,310^-3 радиан).

Зная углы ₀, ₁, _-1, нетрудно найти координаты точек х₂ на плоскости П₂, в которых будут наблюдаться максимумы интенсивностей соответствующих линий пространственного спектра:

.

При  << 1 и в результате расчета можно получить (при = 10 ⁴ мм):

.

Найдем координаты первых нулей амплитудных распределений. Они будут расположены симметрично относительно максимумов нулевого, первого и минус первого порядков и удалены от них на расстояния:

.

Подставив исходные данные в миллиметрах, получим

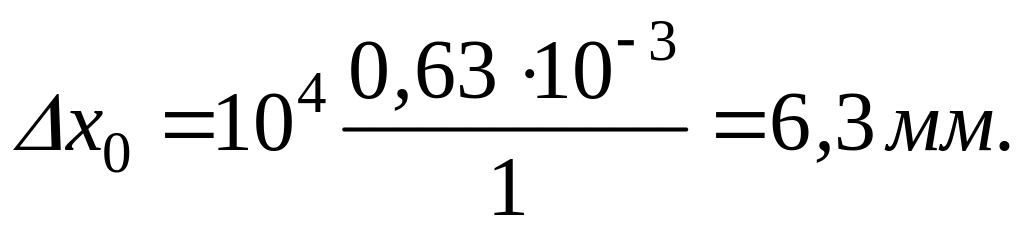
Нередко для наблюдения пространственного спектра используют схему с линзой, изображенную на рис. 1.7.

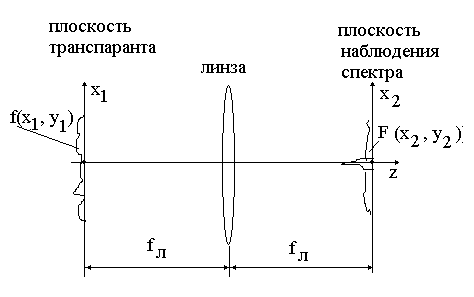
Рис.1.7 . Схема наблюдения пространственного спектра с применением линзы (вариант 1).

В этой схеме транспарант, например дифракционная решетка, располагается в передней фокальной плоскости линзы, а наблюдение и регистрация пространственного спектра проводятся в задней фокальной плоскости линзы. При этом используется замечательное свойство тонкой линзы, в соответствии с которым распределение амплитуд, заданное в передней фокальной плоскости функцией преобразуется при прохождении через линзу так, что в задней фокальной плоскости получается распределение амплитуд , являющееся преобразованием Фурье от . Строго говоря, это соотношение имеет место при бесконечных размерах линзы. Тем не менее, его часто используют при анализе оптических систем, пренебрегая, после соответствующей оценки погрешностями, вызванными конечностью апертуры линзы. Каждой пространственной частоте спектра функции в плоскости П₁ соответствует точка с координатой х₂y₂ в плоскости П₂.

На практике нередко используют другую схему наблюдения пространственного спектра с применением линзы, изображенную на рис. 1.8 , в которой транспарант располагается в непосредственной близости от линзы.

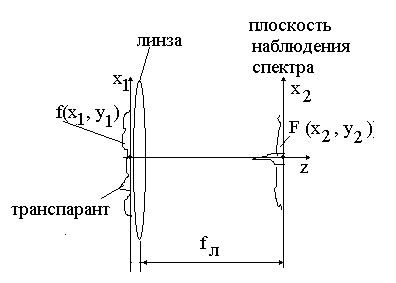
Рис.1.8 . Схема наблюдения пространственного спектра с применением линзы (вариант 2).

В этой схеме полученное в задней фокальной плоскости линзы амплитудное распределение будет отличаться от Фурье преобразования функции лишь некоторым фазовым множителем, вызванным кривизной фазового волнового фронта. Напомним, что приборы регистрируют мощность (интенсивность) излучения. Если регистрировать распределение интенсивности излучения в задней фокальной плоскости, т.е. , то фазовые множители не играют роли. В результате измерений мы получим распределение интенсивности в дифракционной картине, совпадающее с распределением интенсивности в спектре функции . Таким образом, схема, приведенная на рис. 1.8, дает вполне адекватное представление о распределении мощности по пространственному спектру и применяется на практике для наблюдения пространственных спектров. Детальный теоретический анализ эволюции волнового фронта при прохождении его через линзу можно найти в главе 6 монографии [4]