1.5. Энергетические соотношения в пространственном спектре
дифрагированных волн
1.5.1. Интенсивность света. Термином "интенсивность" называют величину, равную квадрату модуля амплитуды волны, т.е. произведению комплексной амплитуды на комплексно сопряженную амплитуду.
(1.28)
Рассмотрим связь между интенсивностью и мощностью излучения.
Если выразить
мощность излучения Р,
прошедшего сквозь щель, через напряженность
электрического поля
,
то в случае равномерно освещенной
апертуры получим следующую формулу :
,
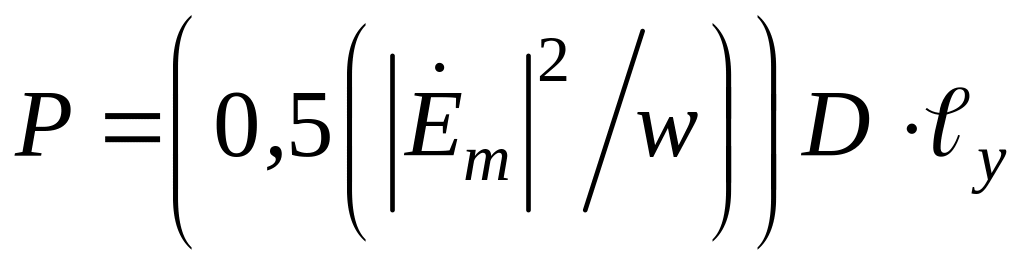(1.29)
где w
− волновое сопротивление среды;
,
− размеры апертуры вдоль осей 0х
и 0у
соответственно;
величина
− площадь излучающей апертуры.
Выражение в скобках
представляет собой плотность мощности
оптического излучения, т.е. иными словами,
мощность в расчете на
единицу площади,
(размерность Вт/м2).
Сравнивая выражения (1.28) и (1.29), можно
заметить, что выражения для интенсивности
и плотности мощности содержат квадраты
амплитуд и отличаются по форме лишь
постоянным множителем. Если положить,
что величина
,
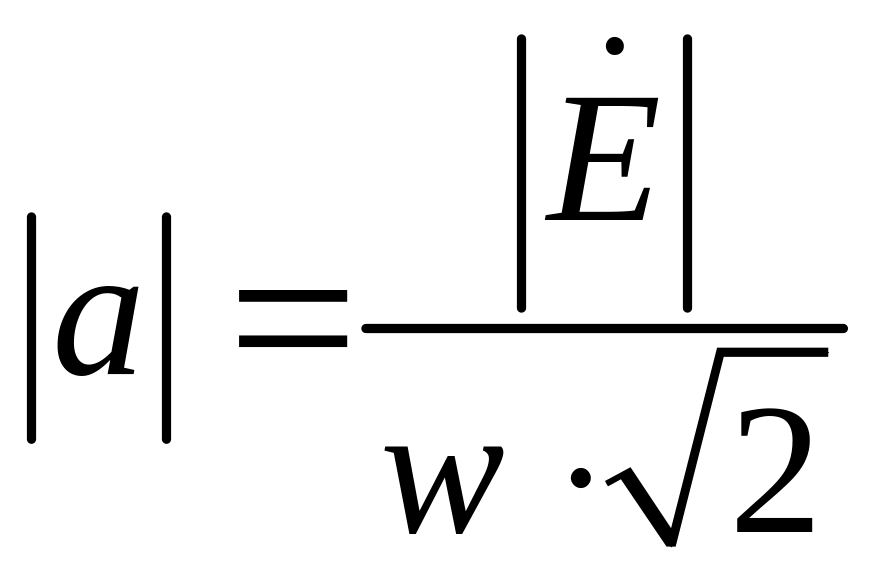то интенсивность будет фактически
тождественна плотности мощности
излучения.
Следует заметить, что для оптических исследований не разработано приборов, которые измеряли бы напряженность электромагнитного поля световой волны. Имеющиеся средства регистрации оптического излучения: фотодиоды, фотоэлементы, болометры и другие выдают на выходе сигнал, зависящий от мощности или энергии излучения, поэтому при анализе оптических схем расчеты интенсивности имеют существенное значение.
1.5.2 Соотношение между мощностью падающего на апертуру и мощностью дифрагированного излучения при дифракции света на щели
Между мощностью световой волны, выходящей из излучающей апертуры, и мощностью, заключенной во всех компонентах пространственного спектра, существует связь, описываемая равенством Парсеваля, см. [4, 8]:
(1.30)
Здесь
− распределение амплитуды волны по
апертуре, а
− распределение амплитуд элементарных
плоских волн в пространственном спектре.
Выражение (1.30) отражает закон сохранения энергии. Мощность, излученная с апертуры, полностью расходуется на создание волн пространственного спектра и равна суммарной мощности всех его компонент.
Рассмотрим,
как выполняется соотношение (1.30) при
дифракции плоской волны на щели. Мощность
волны, прошедшей через апертуру размером
можно рассчитать, вычислив интеграл в
левой части равенства (1.30):
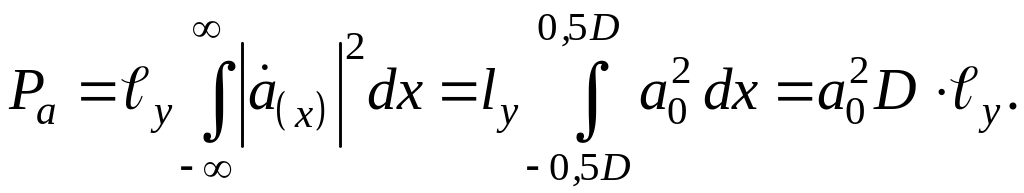(1.31)
Интеграл по пространственным частотам в правой части равенства (1.30) выражает мощность излучения на всех пространственных частотах пространственного спектра. Форма пространственного спектра при дифракции света на щели была найдена ранее (см. формулу 1.22). Подставив (1.22) в интеграл получим:
(1.32)
Из сопоставления выражений (1.31) и (1.32) видно, что соотношение Парсеваля выполняется. При вычислении интеграла (1.32) использовано следующее соотношение, взятое из справочника [18], стр. 192, интеграл 858.652.
.
При п
= 1 и в пределах
получим
.
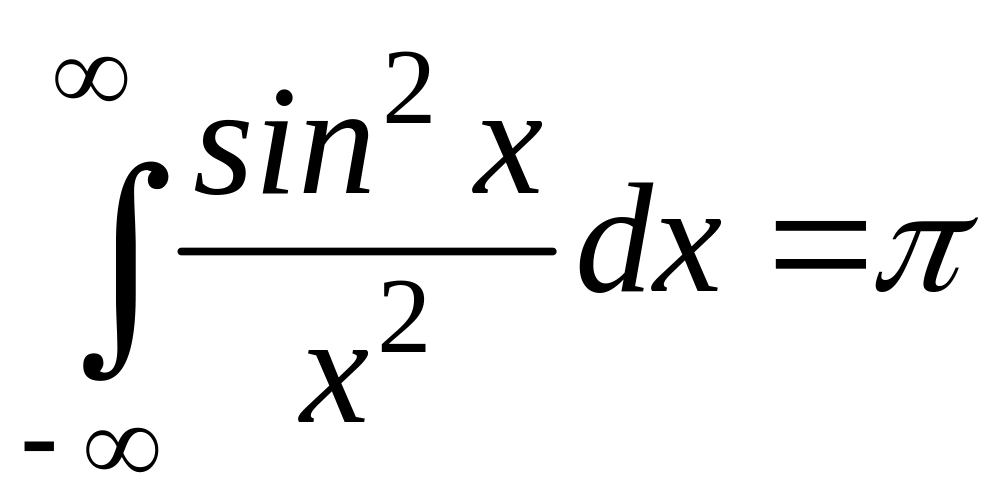