1.4. Примеры расчета пространственных спектров простейших

транспарантов

Задача 1.4.1. Пространственный спектр дифракции оптической волны на щели в непрозрачном экране (рис. 1.2).

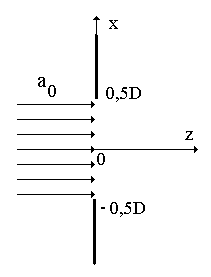
Рис.1.2 Схема прохождения оптической волны через щель.

Пусть однородная волна с амплитудой направлена вдоль оси 0z на щель шириной D в непрозрачном экране. Волновой вектор волны направлен вдоль оси 0z и падающая волна описывается уравнением . Распределение амплитуд в плоскости z = 0 однородно. В направлении оси 0у щель однородная и бесконечная. Функцию пропускания щели запишем:

(1.21)

Пространственный спектр можно найти, применяя формулу (1.11) для

одномерного варианта. При этом интеграл отличен от нуля только в пределах от -0,5 D до 0,5 D.

(1.22)

В литературе (см.[7]) принято обозначать функцию .

Зависимость модуля амплитуды от пространственной частоты, , изображена на рис. 1.3.

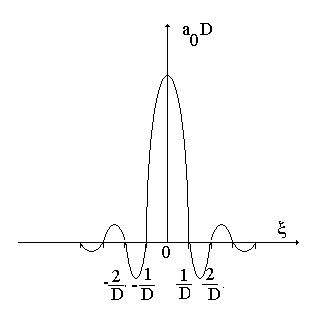
Рис 1.3. Вид пространственного спектра, прошедшего через щель.

Она имеет максимум при = 0. В областях и нули распределения (1.22) расположены в точках, где , т.е. при , . Учитывая, что , нули этого распределения имеют следующие угловые координаты:

; ; , и т.д. (1.23)

Если размер щели увеличить, то, как видно из этих формул, угловая ширина главного максимума уменьшается. При функция в пределе переходит в -функцию, и пространственный спектр волны будет отображаться одной бесконечно тонкой линией.

Задача 1.4.2. Пространственный спектр при дифракции плоской волны на решетке с гармонической функцией пропускания (рис. 1.4).

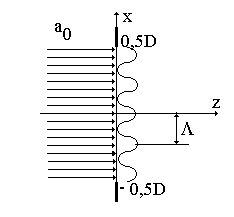
Рис.1.4. Схема к анализу пространственного спектра при дифракции оптической волны на решетке амплитудного типа.

Пусть имеется дифракционная решетка амплитудного типа с периодом , с гармонической зависимостью функции прозрачности от координаты

, (1.24)

т − коэффициент глубины модуляции прозрачности .

Размеры решетки ограничены по координате 0x окном .

Найдем пространственный спектр излучения при освещении решетки (1.24) плоской волной с амплитудой , направленной вдоль оси 0z.

Амплитудное распределение волны после прохождения решетки описывается выражением:

(1.25)

Пространственный спектр будем рассчитывать с помощью интеграла (1.11) при подстановке (1.25) под знак интеграла

(1.26)

При вычислении (1.26) каждый из трех интегралов сводится фактически к предыдущему интегралу (1.22). Вычисление (1.25) дает:

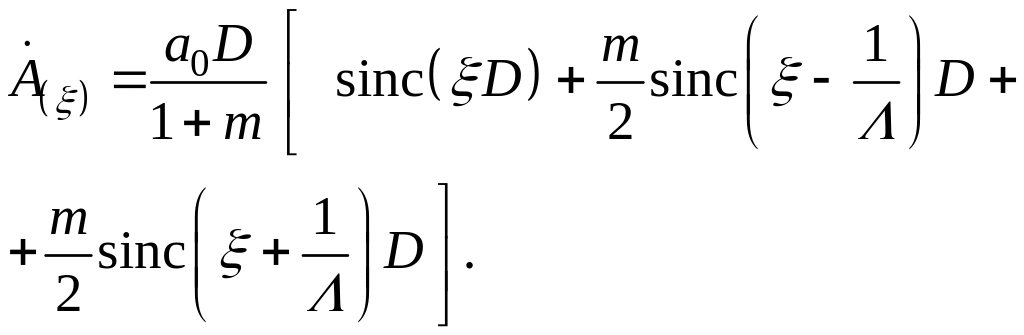(1.27)

Распределение амплитуд в пространственном спектре изображено на рис. 1.5.

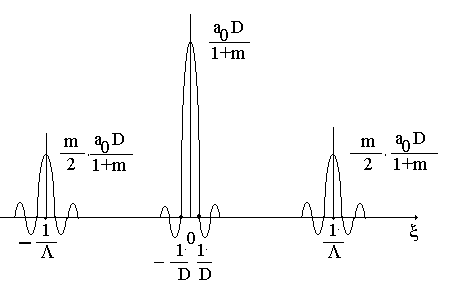
Рис.1.5. Вид пространственного спектра оптической волны после дифракции на амплитудной гармонической решетке.

Пространственный спектр волны, прошедшей через амплитудную гармоническую решетку с периодом , состоит из трех линий: центральной и двух боковых. Центральный максимум находится на нулевой пространственной частоте, а боковые максимумы сдвинуты относительно центрального максимума на величины и . Амплитуды боковых максимумов пропорциональны величине глубины модуляции амплитудной решетки т.

Полуширина каждого из трех максимумов определяется размером окна D и равна, как и в случае щели без решетки, величине .

При увеличении ширины окна D, т.е. протяженности решетки вдоль оси 0х линии пространственного спектра сужаются и в пределе при превращается в -функции, расположенные на частотах .