4.4. Опознавание образов с применением Фурье- голограммы.

Задача опознавания образа формулируется так: пусть имеется некоторое количество знаков, картинок, которые представлены в виде плоских транспарантов (фотографий), прозрачность которых обозначим , а также имеется некоторый эталонный знак из этого набора. Сравнивая знаки из набора с эталонным знаком, поставим задачу найти в этом наборе знаки, которые похожи на эталонный знак. Набор знаков условно можно назвать алфавитом. Как известно, степень сходства двух сигналов можно установить, если найти их взаимную корелляцию. Эта задача может быть решена с помощью оптической схемы, изображенной на рис.4.10.

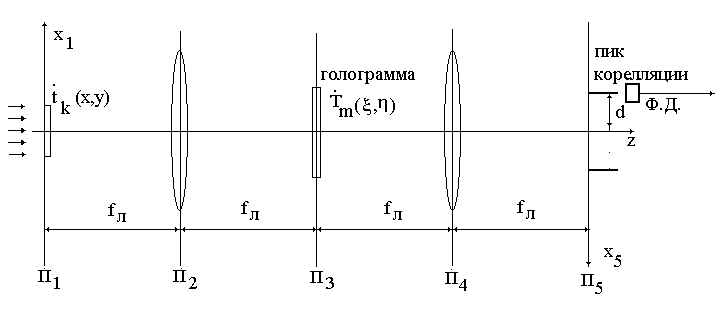
Рис 4.10. Схема опознавания образа из множества.

В плоскости , в передней, помещают транспаранты распознаваемых знаков (образов). В плоскости , в задней фокальной плоскости линзы, помещают голограмму эталонного знака , которая заранее записана по методу записи Фурье- голограммы с применением схемы, изображенной на рис. 4.8. Голограмма, установленная в плоскости просвечивается световым потоком, амплитудно- фазовое распределение которого является Фурье образом функции пропускания транспаранта , установленного в плоскости . За голограммой получаем амплитудно- фазовое распределение, которое является произведением Фурье- образа транспаранта, установленного на входе схемы, на функцию пропускания голограммы. Далее волна проходит через вторую линзу и в её задней фокальной плоскости формируется Фурье- образ волны, полученной справа от голограммы. Корелляционный пик формируется в плоскости в области, находящейся на расстоянии, равном d от оптической оси. Запишем ряд соотношений, которые более точно описывают процесс распознавания образов. По аналогии с формулой 4.22 запишем функцию пропускания голограммы эталонного образа:

(4.27)

Обозначим через Фурье-образ функции пропускания транспаранта . Положим, что световая волна на входе схемы имеет единичную амплитуду. В этом случае амплитуда волны за голограммой может быть представлена выражением:

(4.28)

После перемножения получим:

Рассмотрим четвертое слагаемое этого выражения:

(4.29)

Можно показать, что произведение Фурье-преобразования на сопряженное Фурье-преобразование является Фурье-образом функции корелляции двух исходных функций.

Функция корелляции двух функций имеет вид:

. (4.30)

Заменим в формуле (4.30) функцию на её обратное Фурье преобразование:

(4.31)

Подставив (4.31) в формулу (4.30) изменив порядок интегрирования, получим:

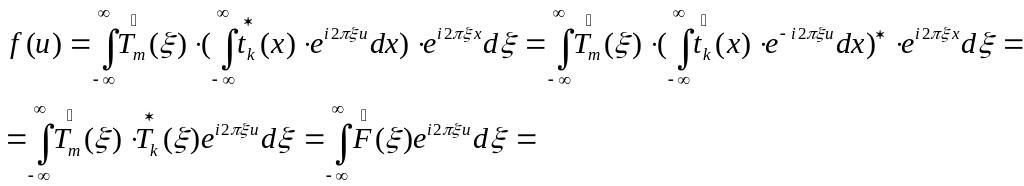
Последнее выражение- это формула обратного преобразования Фурье.

В результате мы получили:

(4.32)

В результате Фурье- преобразования функции корелляции двух функций мы получаем функцию , равную произведению Фурье- образов этих функций. При обратном Фурье- преобразовании мы получим функцию корелляции исходных образов. Дополнительный экспоненциальный множитель даст при Фурье- преобразовании смещение по координате x на величину d.

Запишем Фурье- преобразование от выражения (4.29).

(4.32)

В последнем выражении произведена замена переменной: . Как видно из формулы (4.32), на выходе в плоскости мы получили полезный сигнал в виде функции корелляции двух образов в перевернутой системе координат . Функция корелляции смещена относительно начала координат на расстояние, равное d, . При условии, что символ, помещенный в плоскости , имеет одинаковую конфигурацию с символом, записанным на голограмму, мы будем наблюдать в точке максимально яркое световое пятно, которое соответствует функции автокорелляции символа записанного на голограмме транспаранта. Световое пятно направляют на фотодетектор, с выхода которого получают электрический сигнал, по уровню которого можно сделать вывод о степени сходства образа с эталоном.

Приложение к разделу 4 «основы голографии». Некоторые формулы.

Преобразование Фурье функции имеет вид:

, (П₁)

обратное преобразование Фурье:

, (П₂)

свертку двух функций определяют формулой :

. (П₃)

Функцию корелляции двух функций определяют формулой:

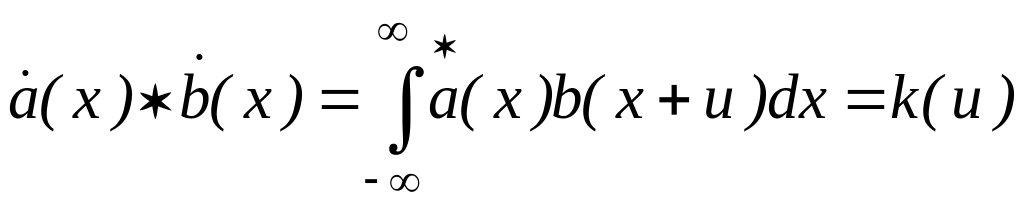. (П₄)

Если функция тождественна функции , то операция корелляции называется операцией автокорелляции:

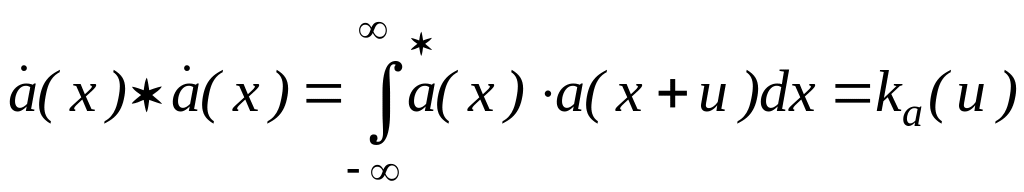. (П₅)

Анализ формулы третьего слагаемого выражения (1.7)

Запишем Фурье-интеграл от функции

, (П6)

а затем функцию заменим ее обратным Фурье преобразованием и изменим порядок интегрирования:

(П₇)

Преобразуем интеграл, стоящий в скобках:

(П₈)

Подставив полученное выражение П₈ в П₇, получим:

. (П₉)

Можно провести замену переменных:

. (П₁₀)

Затем следует привести формулу (П₉) к виду, подобному (П₅):

. (П₁₁)

Отсюда видно, что спектр функции равен функции автокорелляции функции , сдвинутой относительно начала координат на величину .

* см. [8], стр. 45, дельта-функция как предел.

* В англоязычной технической литературе эта величина называется responsivity и обычно обозначается буквой R. Тогда i_ф = RP.

* ^* Спектр решетки совпадает фактически с пространственным спектром плоской волны с единичной амплитудой, прошедшей через решетку.

* См. И.И. Бронштейн, К.А. Семендяев. Справочник по математике. М.: Наука, 1986. – С. 419.

1 С изложением строгого вывода формулы дифракционного интеграла можно ознакомиться в книгах:

1) Шеффер. Теоретическая физика, том Ш, часть 2. Оптика. ГОНТУ НКТП СССР, 1938.

2) Маркузе Д. Оптические волноводы. Изд-во «Мир», М., 1974. Глава 2.

1 )Теорема о сдвиге. ; тогда

118