4.1.4. Анализ пространственного спектра восстановленных волн

Выполним Фурье-преобразование выражения (4.7) и будем анализировать полученное выражение, описывающее пространственный спектр восстановленных волн. Ввиду того, что множитель в (4.7) одинаков для всех членов, мы не будем записывать его в дальнейшем. Картина распределения амплитуд пространственного спектра волн после голограмм изображена на рис.4.6

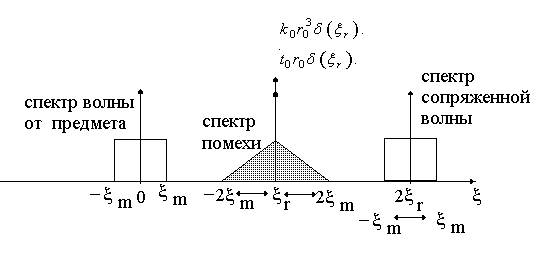
Рис 4.6 .Пространственный спектр восстановленных волн от голограммы, построенный в соответствии с выражением (4.7) .

Первое слагаемое в выражении (4.7) восстановленной волны − это "остаток" плоской опорной волны, прошедшей через голограмму. Фурье-преобразование (спектр) этого слагаемого имеет вид дельта функции:

. (4.8)

Аналогичный вид имеет Фурье-преобразование второго слагаемого:

. (4.9)

Эти составляющие пространственного спектра изображены на рис.4.6 в виде вертикальных стрелок.

Пространственный спектр восстановленной волны соответствует четвертому члену в выражении 4.7. Функция является Фурье преобразованием функции .

. (4.10)

Положим, что занимает участок пространственного спектра от частоты до в районе нулевой пространственной частоты. На рисунке 4.6. он изображен в форме прямоугольника и соответствует пространственному спектру волны, исходящей от предмета.

Пространственный спектр сопряженной волны ( соответствует пятому слагаемому в выражении 4.7) занимает участок в районе пространственной частоты от частоты до частоты . Для доказательства этого рассмотрим выражение пятого слагаемого (4.7):

(4.11)

и найдем Фурье образ (4.11), выразив его через известный нам Фурье образ . Для простоты рассмотрим функцию одной переменной . Пусть имеет Фурье преобразование

, т.е. 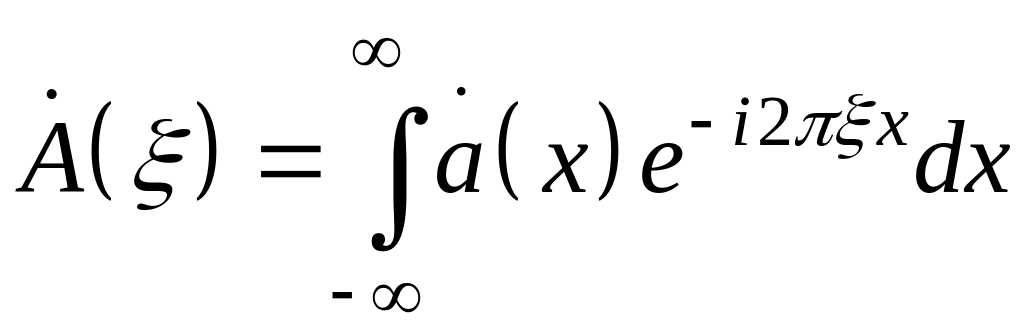. (4.12)

Выразим Фурье преобразование сопряженной функции

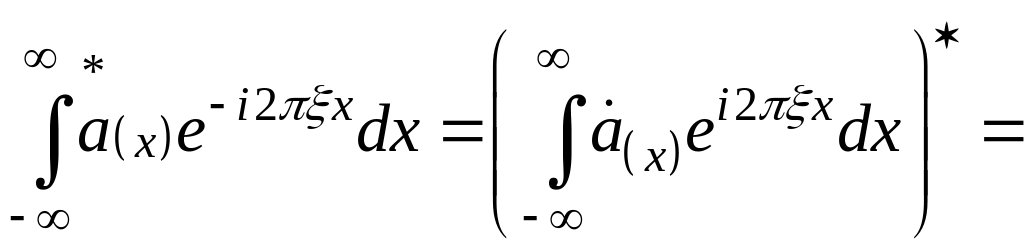
. (4.13)

Значок * здесь означает сопряжение.

. (4.14)

Таким образом, показано каким способом Фурье образ сопряженной функции можно выразить через Фурье образ функции :

если , (4.15)

то .

Операция сопряжения и оборота оси координат (замена  на -) не изменяют ширины спектра. В нашем простейшем случае конфигурация спектра (форма прямоугольника) сохраняется. Однако в выражении (4.11) кроме величины и постоянного множителя присутствует множитель . Известно, что умножение функции на экспоненциальный множитель такого вида приводит к сдвигу¹⁾ спектра этой функции. В данном случае пространственный спектр сдвинут на величину по оси частот. В результате функция будет иметь Фурье образ вида:

. (4.16)

Формулу (4.16) можно получить и другим путем:

(4.20)

Таким образом, на шкале пространственных частот диаграмма пространственного спектра сопряженной волны изображается прямоугольником с протяженностью с центром на пространственной частоте .

Исследование формы пространственного спектра третьего члена выражения (4.7), который имеет вид , дает следующую картину. Форма этого спектра имеет вид автокорелляции функции , и эта функция сдвинута на величину относительно точки начала координат .

Если спектр сигнала имеет форму прямоугольника (рис. 4.6), то спектр третьего слагаемого имеет форму симметричного равнобедренного треугольника, ось симметрии которого проходит через точку . Спектр занимает полосу пространственных частот от до , и имеет ширину . Вывод выражения, которое определяет форму спектра третьего слагаемого , приведен ниже.

Некоторые определения и формулы.

Преобразование Фурье функции имеет вид:

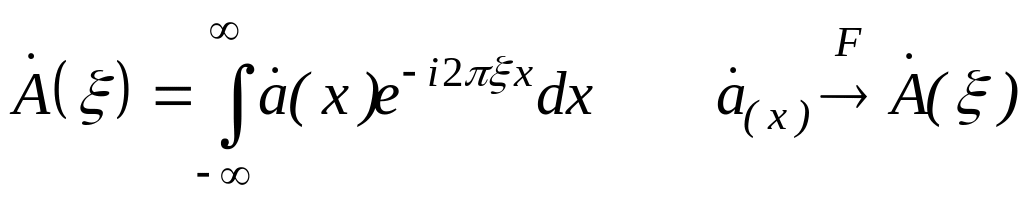, (4.21)

обратное преобразование Фурье:

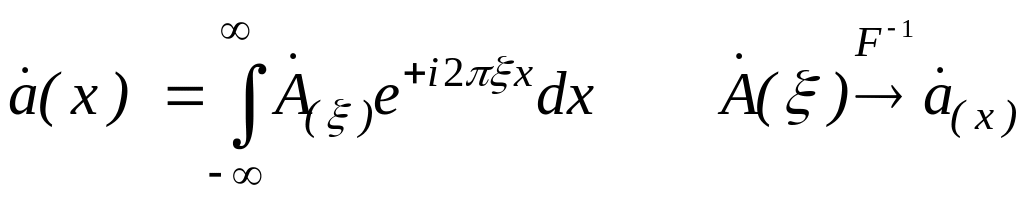, (4.22)

свертку двух функций определяют формулой :

. (4.23)

Функцию корелляции двух функций определяют формулой:

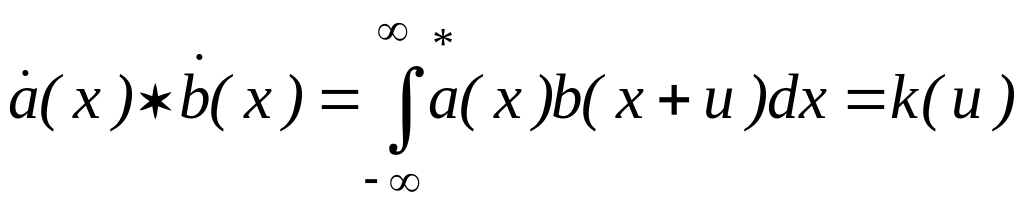. (4.24)

Если функция тождественна функции , то операция корелляции называется операцией автокорелляции:

. (4.25)

Анализ формулы третьего слагаемого выражения (1.7)

Запишем Фурье-интеграл от функции

, (4.26)

а затем функцию заменим ее обратным Фурье преобразованием и изменим порядок интегрирования:

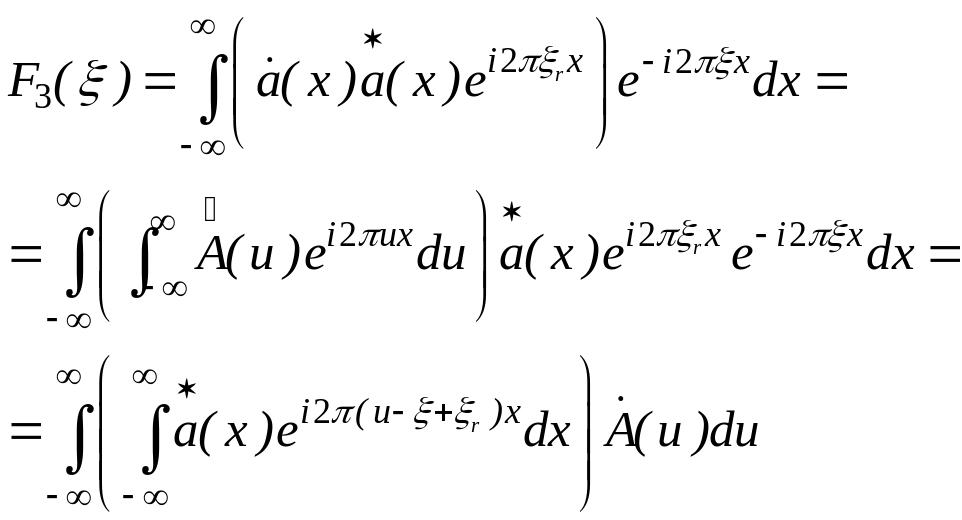(4.27)

Преобразуем интеграл, стоящий в скобках:

(4.28)

Подставив полученное выражение (4.28) в (4.27), получим:

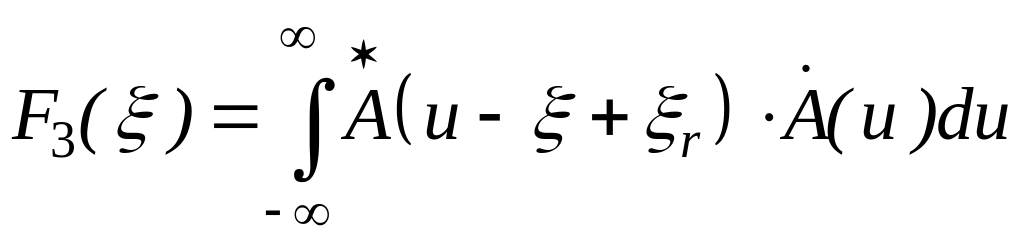. (4.29)

Можно провести замену переменных:

. (4.30)

Затем следует привести формулу (П₉) к виду, подобному (П₅):

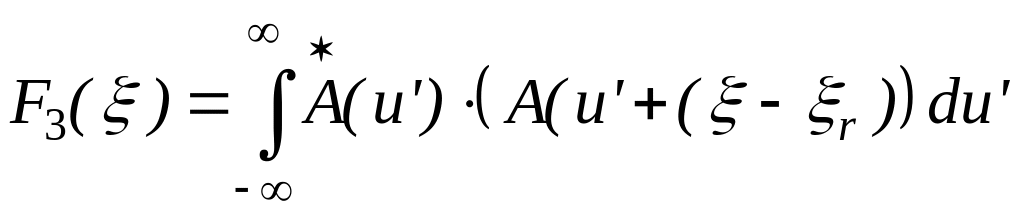. (4.31)

Отсюда видно, что спектр функции равен функции автокорелляции функции , сдвинутой относительно начала координат на величину .

Выводы, которые можно сделать на основе проведенного анализа пространственного спектра дифрагированных волн.

- Для того, чтобы наблюдать восстановленное изображение без помех, необходимо, чтобы спектр восстановленной волны не перекрывался со спектром помехи. Для этого следует выбрать пространственную частоту опорной волны в соответствии с условием: . Этот вывод легко сделать из анализа рис. 4.6.

-Вместе с тем, условие предъявляет повышенные требования к разрешающей способности фотопластинки, на которой записывают голограмму. Для того, чтобы при условии записать интерференционную картину, образованную опорной волной и крайней левой составляющей спектра предметной волны на пространственной частоте - необходимо иметь разрешающую способность фотоматериала не менее, чем 4 , т.е. не менее чем разность между пространственной частотой опорной волны и наиболее удаленной от нее пространственной частотой предметной волны. В то же время следует напомнить, что при обычной фотографии достаточная величина разрешающей способности равна . Таким образом, для голографической записи оптического сигнала необходимы регистрирующие среды (в частности фотопластинки), имеющие значительно более высокую разрешающую способность, чем обычные регистрирующие среды, применяемые для фотографии. Специальные голографические фотопластинки имеют разрешающую способность порядка нескольких тысяч линий на миллиметр.

4.2. Схема голографии по методу Ю. Н. Денисюка.

В предыдущем разделе мы считали, что в результате интерференции двух когерентных световых пучков на голограмме записывается некоторая совокупность интерференционных полос, а фотоэмульсия, т.е. среда , в которой записывается голограмма, имеет малую толщину, например, порядка длины волны лазерного излучения. Ю.Н. Денисюк в 1962 году предложил использовать для записи голограмм толстослойную эмульсию, толщина которой составляет несколько десятков длин волн оптического излучения. Запись цветных фотографий на толстослойной эмульсии была ранее продемонстрирована Г. Липманом в конце 19 века. В экспериментах Липмана толстослойная фотоэмульсия располагалась на поверхности ртутного зеркала. При освещении этой системы в толще светочувствительной фотоэмульсии существуют две встречные волны: прямая и отраженная. В результате в толще эмульсии записывается система интерференционных поверхностей, отстоящих друг от друга на расстоянии порядка половины длины световой волны в среде фотоэмульсии ( , где n- показатель преломления среды). При восстановлении изображения, когда свет падает на эту систему интерференционных поверхностей, происходит сложение многочисленных элементарных волн, отраженных от каждого слоя и суммарный коэффициент отражения во много раз больше отражения от одного слоя. При этом система слоев обладает избирательностью. Строго синфазное сложение волн происходит только на некоторой резонансной длине волны, т.е. на длине волны записи. Если длина волны сильно отличается от резонансной, то коэффициент отражения невелик по сравнению с резонансным. Таким образом, существует эффект цветовой избирательности.

Схема голографии Денисюка изображена на Рис 4.8. Опорный пучок в этой схеме направлен навстречу предметному пучку. Толщина слоя эмульсии голограммы достаточно велика по сравнению с длиной волны лазерного излучения и составляет, например, порядка 10 микрометров.

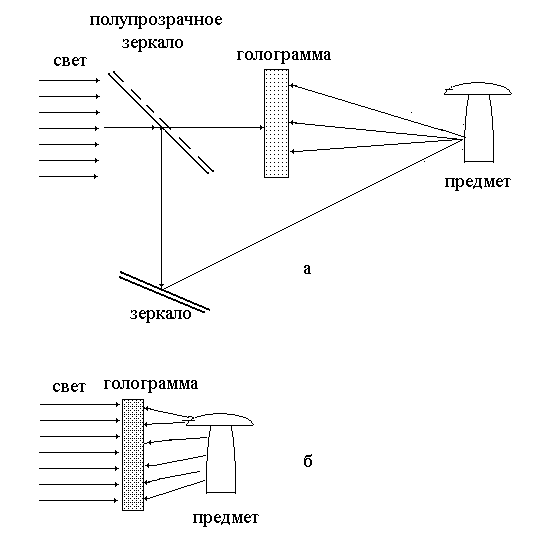
Рис.4.7. Схемы записи голограмм по методу Ю.Н. Денисюка. Опорная волна направлена навстречу или приблизительно навстречу сигнальной волне.

В схеме (а) оптический пучок от источника разделяется полупрозрачным зеркалом на два пучка, один из которых является опорным, а второй после отражения от зеркала направляется на освещение объекта. В схеме (б) опорная волна проходит сквозь фотопластинку, отражается от предмета и таким образом формируется предметная волна.

При восстановлении голограммы Денисюка её освещают в направлении опорной волны. Для освещения может использоваться даже белый свет. При этом происходит восстановление предметной волны, так как голограмма обладает способностью отфильтровывать излучение с теми длинами волн, которые были использованы при записи.