3.6 Акустооптические схемы с линзами, предназначенные для оптической обработки радиосигналов.

3.6.1. Вводные замечания. Рассмотрим здесь две 000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000акустооптические схемы обработки радиосигналов, которые могут выполнять операцию анализа спектра и операцию свертки радиосигналов. Эти схемы обычно включают в себя три важных компонента.

• Пространственный модулятор когерентной световой волны, который преобразует функцию, описывающую радиосигнал, в соответствующую ей функцию пространственной модуляции волнового фронта световой волны. Эту функцию выполняет акустооптическая ячейка.

• Линза, выполняющая преобразование Фурье оптического сигнала;

• Фотодиод или набор (линейка) фотодиодов, которые преобразуют оптический сигнал в электрический сигнал на выходе схемы.

Пространственный модулятор. В качестве пространственного модулятора применяется акустооптическая (А.О.) ячейка. На рис 3.7 изображена схема А.О. ячейки, в которой используется эффект дифракции света на акустической (ультразвуковой) волне, т.е. схема дифракции Рамана-Ната. Возбудитель 1 представляет собой пластину, вырезанную из кристалла, обладающего пьезоэлектрическим эффектом или пластину из пьезокерамики. На обеих сторонах пластины нанесены металлические электроды. Возбудитель плотно связан со звукопроводом с помощью слоя индия или с помощью специального клея. Радиосигнал подается на электроды возбудителя ультразвуковых колебаний. Несущая частота радиосигнала находится в области резонанса механических колебаний возбудителя. При этом относительная ширина полосы частот возбудителя обычно велика, так как возбудитель сильно нагружен, и при этом значительная доля энергии колебаний передается в звукопровод. Колебания пластины возбуждают в звукопроводе бегущую со скоростью V акустическую волну. На противоположном конце звукопровода располагается поглотитель акустической волны, чтобы предотвратить помехи, которые может вызвать волна, отраженная от торца звукопровода.

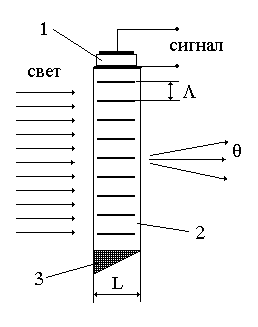
Рис.3.7. Схема акустооптической ячейки, работающей в режиме

Рамана-Ната. 1- пьезоэлектрический возбудитель ультразвуковой волны,

2- звукопровод, 3-поглотитель ультразвуковой волны.

В результате прохождения через акустооптическую ячейку когерентная оптическая волна с длиной волны получает пространственную фазовую модуляцию в соответствии с радиосигналом, который подан на электроды возбудителя. Так, например, если сигнал имеет вид:

, (3.40)

то выражение, описывающее пространственную фазовую модуляцию волнового фронта оптической волны на выходе акустооптической ячейки, работающего в режиме Рамана-Ната, имеет вид:

(3.41)

Здесь - коэффициент, связывающий возмущения фазы волнового фронта с амплитудой сигнала.

Напомним, что режим Рамана-Ната имеет место при условии:

В выражении (3.41) мы использовали приближение малой амплитуды пространственной фазовой модуляции волнового фронта, вызванной акустической волной, так как при малых глубинах модуляции схема находится в линейном режиме. При малой амплитуде фазовой модуляции каждой частоте радиосигнала будет соответствовать определенный набор пространственных частот пространственного спектра и определенные углы направления дифракции первых порядков:

(3.42)

3.6.2.Схема акустооптического анализатора спектра радиосигналов.

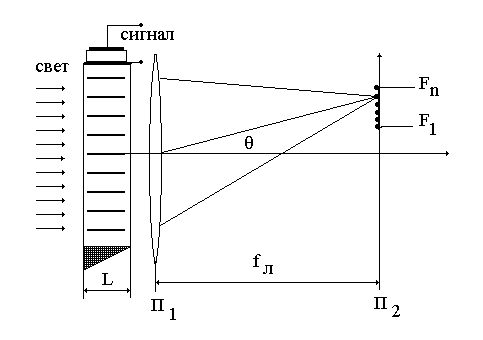
Рис.3.8. Схема акустооптического анализатора спектра радиосигналов.

Положим, что в схеме акустооптического анализатора спектра, которая изображена на рис.3.8, на вход возбудителя подан монохроматический радиосигнал с частотой . В звукопроводе возбуждается акустическая волна с длиной волны . В результате формируется дифрагированная оптическая волна, направленная под углом :

(3.43)

Эта волна дает отклик на плоскости в виде дифракционного пятна в точке с координатой, которую в приближении малых углов дифракции можно выразить формулой:

(3.44)

Каждой частоте соответствует точка на плоскости . В этих точках расположены фотодетекторы, и с выхода каждого из фотодетекторов снимают электрический сигнал, соответствующий частоте .

Оценим предельную разрешающую способность данного анализатора. Размер дифракционного фокального пятна можно оценить как

(3.45)

Здесь D- поперечный размер оптического пучка, k- коэффициент который может быть порядка 1.

При практическом конструировании схемы желательно, чтобы размер фокального пятна и размер фотодетектора совпадали. Положим, что расстояние между соседними фотодетекторами составляет величину порядка размера фокального пятна, . Тогда, взяв дифференциал из (3.44) и приравняв , с учетом (3.45) можно получить:

(3.46)

Здесь - разрешающая способность анализатора, - время прохождения акустической волны через апертуру оптического пучка.

Проведем простую количественную оценку. Пусть в качестве материала звукопровода выбран плавленый кварц. Скорость распространения продольной звуковой волны составляет м/c. При размере апертуры D=1см, 1,6 мкс и при k=1,22 получим .

Важным параметром устройства является число разрешаемых точек в пределах рабочего диапазона. Диапазон частот, в котором может работать данная схема, ограничена полосой частот возбудителя акустических волн. Полоса частот составляет некоторую долю, возможно, порядка 20-30% от центральной резонансной частоты. Зная можно оценить число разрешаемых точек N:

(3.47)

Если 60мГц, а , то число N=100. В последней формуле можно подставить полосу в мегагерцах, а длительность в микросекундах.

Важной особенностью схемы акустооптического анализатора спектра радиосигналов является очень малое время, необходимое для получения результатов. Практически оно составляет величину порядка , т.е. порядка времени прохода акустической волны через звукопровод. В подобных случаях принят термин: «анализ в реальном масштабе времени».