3.3 Анализ оптической схемы из транспаранта и линзы.

3.3.1.Функция пропускания тонкой линзы. Для анализа нам необходимо будет описать функцию прозрачности линзы, т.е. функцию преобразования волнового фронта при прохождении его через тонкую линзу. С этой целью рассмотрим оптическую схему, изображенную на рис. 3.3.

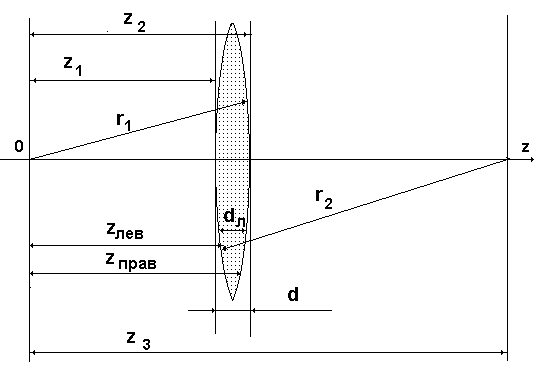
Рис 34.3 Схема для расчета фазовой задержки оптической волны в линзе.

Тонкая линза, изготовленная из прозрачного материала с показателем преломления, равным , окружена воздухом с показателем преломления . Толщина линзы намного меньше, чем радиусы поверхностей r₁ и r₂, образующие линзу. Важное условие состоит в том, что материал линзы прозрачен и не поглощает излучения. При отсутствии поглощения линза представляет собой фазовый транспарант, функцию пропускания которого можно выразить в виде:

(3.16)

Здесь функция отражает зависимость фазовой задержки оптической волны от координат x и y при ее прохождении от плоскости до плоскости , касательных плоскостей к выпуклостям линзы.

Проведем расчет фазовой задержки , которая складывается из фазовой задержки в толще материала линзы c показателем преломления и фазовой задержки в воздушных промежутках между поверхностями, образующими линзу, и плоскостями и . Толщину линзы, d_л (х, у) , в произвольной точке с координатами х и у найдем, рассчитав разность между координатами z правой и левой сферических поверхностей.

d_л ( х , у) = , (3.17)

где

, (3.18)

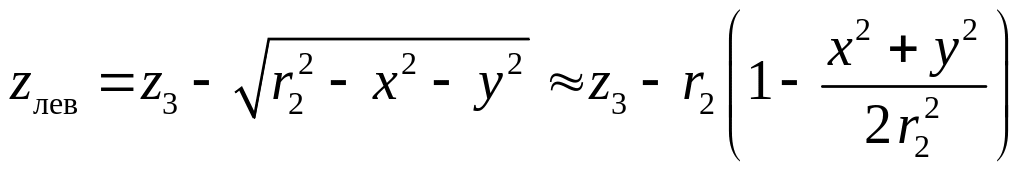. (3.19)

Здесь z₃ – координата центра сферы с радиусом r₂ по отношению к точке , где расположен центр сферы с радиусом r₁.

Замена квадратного корня приближенным выражением справедлива в случае параксиального приближения. При этом предполагается,

что . С учетом сделанных приближений толщина материала линзы в области с координатами составит:

d_л (х, у)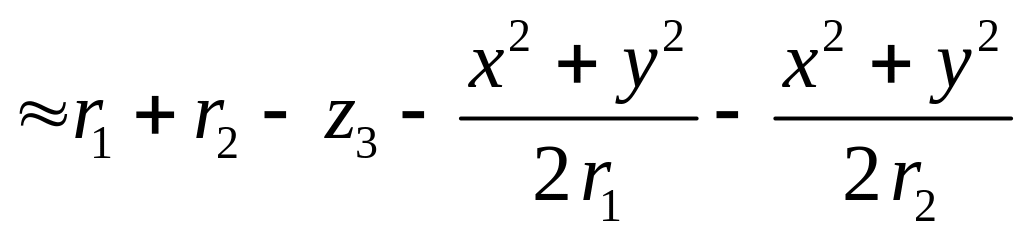 . (3.20)

Фазовая задержка световой волны с длиной волны  в материале

линзы составит:

. (3.21)

Фазовая задержка в воздушном промежутке между плоскостями и и поверхностями линзы составит:

, (3.22)

где d - расстояние между плоскостями и , а величина - длина воздушного промежутка.

Суммируя и , найдем полный фазовый сдвиг световой волны при ее прохождении от плоскости до плоскости , он составит:

. (3.23)

Второе слагаемое не зависит от координат х, у и фактически обозначает неизменный фазовый сдвиг при прохождении волны от одной плоскости до другой. Поскольку этот сдвиг равносилен изменению начала отсчета световой волны, он не влияет на функции преобразования волнового фронта в оптической схеме, и его можно отбросить. После этого с учетом формулы (3.20) получим следующую формулу, выражающую зависимость фазового запаздывания волны в тонкой линзе от координат х , у.

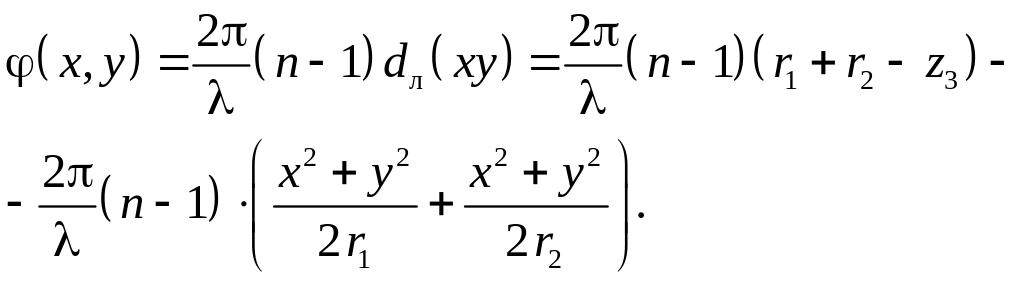(3.24)

В этом выражении первое слагаемое также представляет постоянный фазовый сдвиг, не зависящий от переменных х, у. Отбросив это слагаемое, получим:

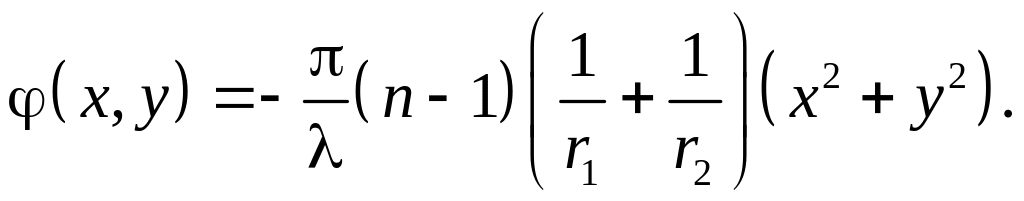(3.25)

Из геометрической оптики известно соотношение, связывающее оптическую силу линзы D_л с радиусами сферических поверхностей, образующих линзу.

(3.26)

С учетом выражений (3.25) и (3.26) формулу, характеризующую комплексную функцию пропускания линзы (3.16) можно записать в такой форме:

(3.27)

Следовательно, тонкая линза является фазовым транспарантом, который преобразует волну с плоским фронтом (на входе слева) в волну с волновым фронтом в форме параболоида вращения.