3.2. Предельный переход к дифракции Фраунгофера.

В формуле (3.3) преобразуем разности квадратов в степени экспоненты подынтегрального выражения. Представим интеграл (3.3) в следующем виде:

(3.4)

В этом выражении множитель, содержащий в показателе экспоненты величины и вынесен за знак интеграла, так как х₂ и у₂ не являются переменными интегрирования. При некотором дополнительном условии подынтегральное выражение можно упростить, положив, что . Это справедливо при условии, что показатель степени экспоненты очень мал, т.е. при условии:

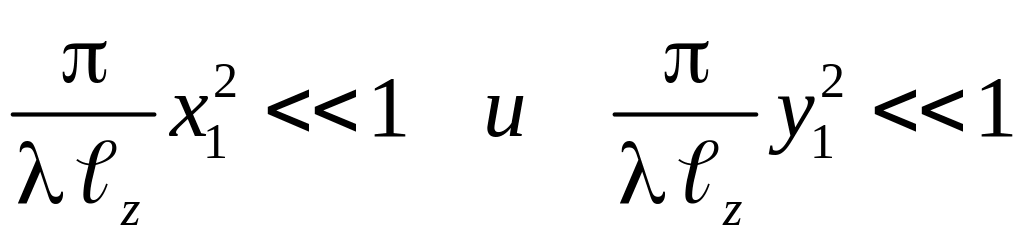. (3.5)

Рассмотрим пример, когда апертура представляет собой квадратную площадку размером стороны, равном D. В этом случае величина , а наибольшие значения переменных x , y будут следующими: .

С учетом этого условия формулу (3.5) можно записать:

(3.6)

Отсюда следует условие

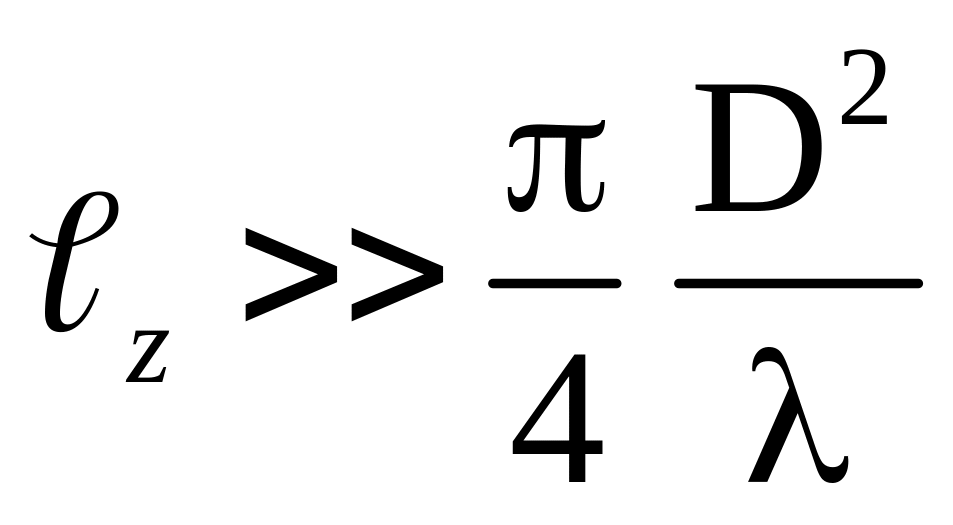. (3.7)

Приближенно это условие записывают в виде:

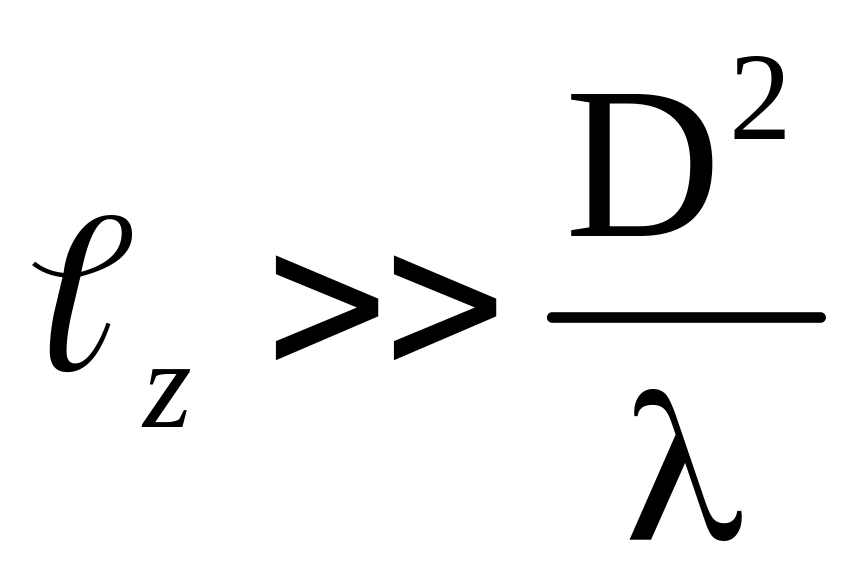. (3.8)

При этом условии, которое называют условием перехода к дальней зоне поля излучения, а по другой терминологии к зоне Фраунгофера , интеграл (3.4) имеет следующий вид:

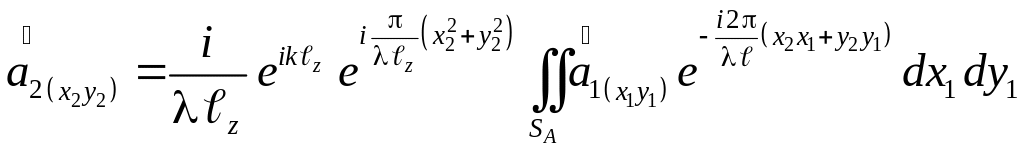. (3.9)

Перед интегралом мы имеем ряд множителей. Группа множителей является константой, которая не зависит от координат х₂, у₂. Множитель является чисто фазовым, он описывает параболическую кривизну волнового фронта в плоскости .

Двойной интеграл по площади апертуры S_A можно преобразовать к виду, который будет фактически преобразованием Фурье от распределения амплитуд поля на апертуре . С этой целью сделаем следующие преобразования:

во-первых: распространим пределы интегрирования на всю плоскость х₁у₁, т.е. от до . Это можно сделать, так как за пределами апертуры поле излучения отсутствует при ;

во-вторых: величины и преобразуем следующим образом:

(3.10)

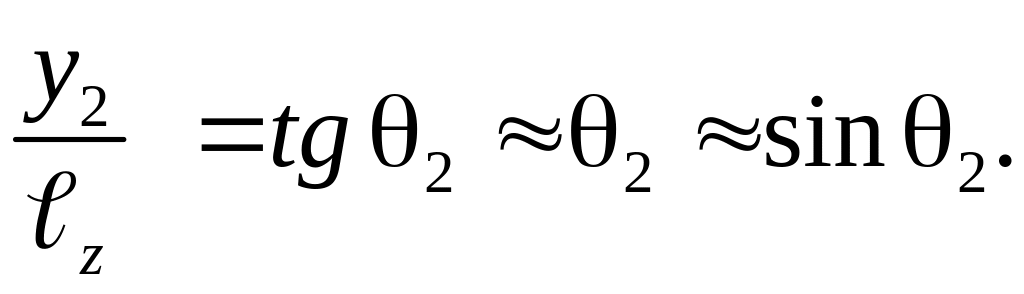(3.11)

Это приближение можно считать допустимым при малых величинах углов ₁ и ₂. Напомним, что мы ранее приняли условие о том, что рассматривается параксиальное приближение. При этом углы дифракции, ₁, ₂ мы полагаем малыми. Тогда с учетом (3.10) и (3.11) можно записать:

. (3.12)

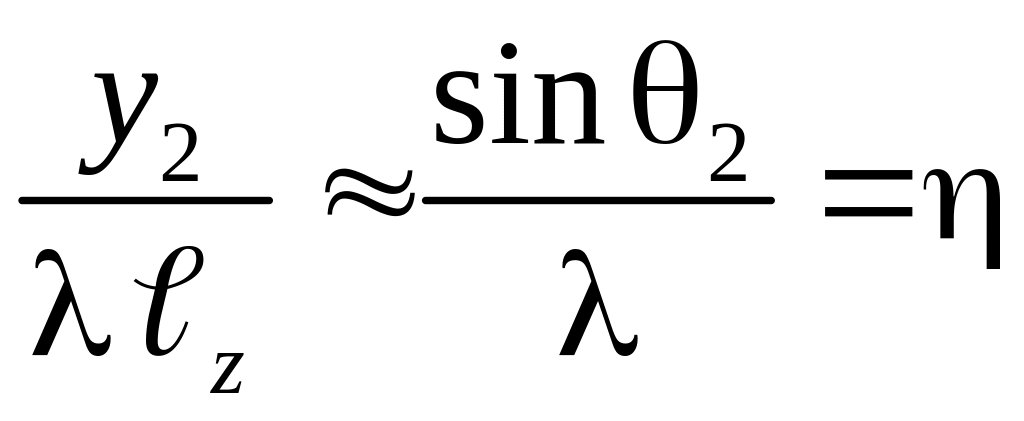. (3.13)

Здесь  и  в соответствии с ранее данными определениями являются пространственными частотами.

Расширим пределы интегрирования за пределы апертуры, до бесконечности, учитывая, что за пределами апертуры амплитуда поля равна нулю. В результате с учетом (3.12) и (3.13) интеграл (3.9) можно записать в виде:

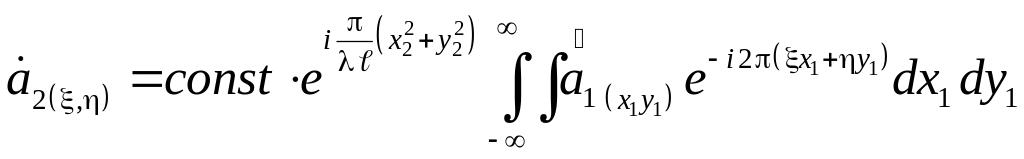. (3.14)

Интеграл в выражении (3.14) представляет собой двумерное преобразование Фурье распределения поля на апертуре.

Если мы поставим задачу исследовать распределение интенсивности (плотности мощности) в дальней зоне, то из выражения (3.14) получим

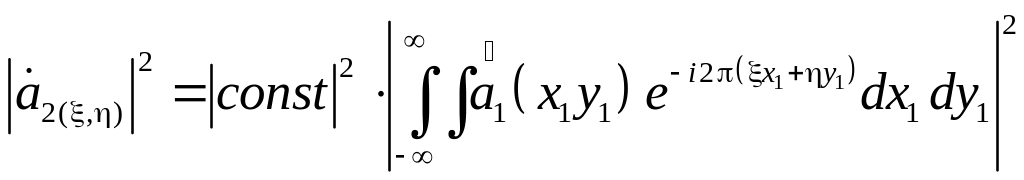, (3.15)

т.е. распределение мощности излучения с точностью до постоянного множителя представляет собой спектр мощности излучения с апертуры.

Составим модель проведения эксперимента по наблюдению пространственного спектра мощности. Рассмотрим простой пример. Допустим, что плоская когерентная волна проходит через квадратное отверстие размером 1мм. на 1мм. Длина волны излучения равна 0,63 микрометра.

Найдем расстояние до области дальней зоны:

Расположим экран на расстоянии, , например на расстоянии 4 метра от отверстия. Будем исследовать распределение плотности мощности излучения на экране. Напомним, что ранее при анализе спектра дифрагированных волн, исходящих от щели с размером, равным D было получено выражение:

При условии, что апертура ограничена также и в направлении координаты Y

Получим для излучения с квадратной апертуры:

На экране мы увидим центральное пятно, обрамленное побочными максимумами в направлениях координат X и Y. Рассчитаем координаты первых нулей . Положим , тогда = .

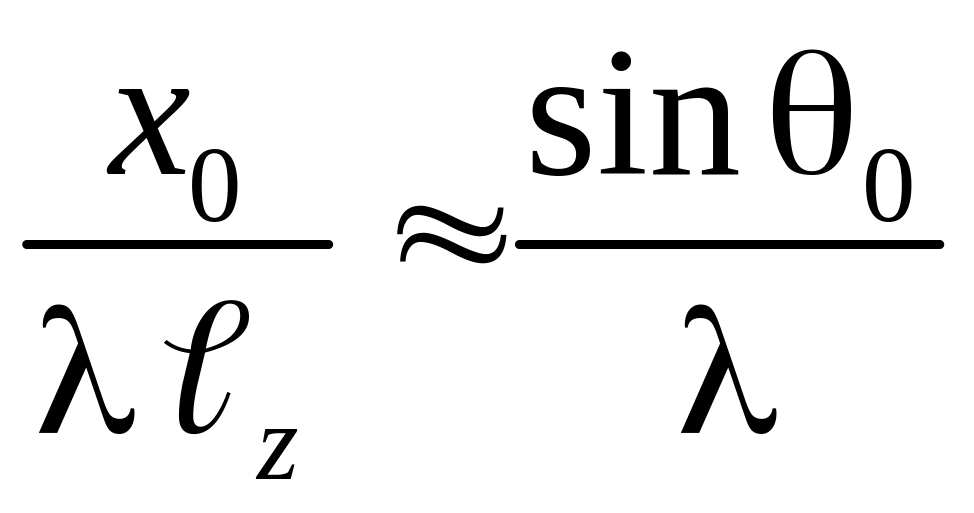Отсюда получим:

Аналогично получим