2.2 Принципы интерферометрии.

Рассмотрим простой пример применения интерферометра для измерения высоты ступеньки на прозрачной пластине. Положим, что в нашем распоряжении имеется пластина, изготовленная из прозрачного материала, а на поверхности этой пластины имеется уступ, высота которого h неизвестна. Задача состоит в том, чтобы измерить высоту этой ступеньки, используя явление интерференции. Для измерений поместим пластину в плечо интерферометра как это показано на Рис 2.2 . Оптические пучки на выходе интерферометра должны быть направлены под небольшим углом один относительно другого. При этом период интерференционных полос должен быть достаточно большим для удобства наблюдения. Заметим, что изображенный на этом интерферометр Рождественского не является единственным вариантом. В промышленном измерительном приборе, который получил название «интерферометр Линника» применена схема типа интерферометра Майкельсона. Описание интерферометра Линника можно найти в [21], а также в интернете.

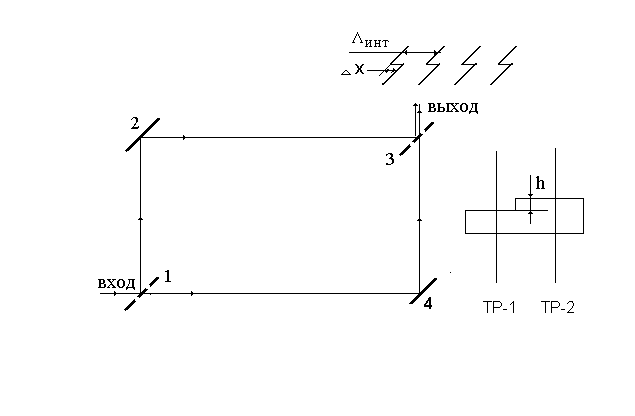
Рис.2.2 Схема измерения высоты ступеньки с помощью интерферометра.

1 и 3-полупрозрачные зеркала, 2 и 4-зеркала с высоким коэффициентом отражения. Образец, изображенный справа помещается в промежуток между зеркалами 3 и 4. Вверху схематически изображены интерференционные полосы в области ступеньки

Разность фаз между лучами, проходящими по нормали к поверхности пластины по траекториям ТР1 и ТР2 справа и слева от границы ступеньки составит:

. (2.19)

Здесь n – показатель преломления материала пластинки.

В результате из-за разницы фазовых сдвигов в районе границы интерференционные полосы сдвинутся на величину

(2.20)

Измерив сдвиг интерференционных полос , рассчитаем высоту ступеньки:

(2.21)

Как видно из этой формулы высота ступеньки выражена через относительную величину сдвига сдвиг интерференционных полос , т.е. величину сдвига в долях периода интерференционной картины. Для расчета необходимо также иметь точные данные о показателе преломления материала пластины.

Проведем простую оценку минимальной высоты ступеньки, которую можно измерить таким способом. Положим, что мы можем надежно измерить величину . Если при этом длина световой волны составляет 0,6 мкм., а показатель преломления равен n=1,6 то минимальная высота ступеньки, которую можно измерить составит 0,1мкм.

2.3. Длина когерентности. Связь между шириной спектра излучения

и длиной когерентности волны.

2.3.1. Вводные замечания. При анализе интерференции мы полагали, что интерференционная картина образована двумя пучками света (плоскими волнами) полученными от одного монохроматического источника, излучение которого не прерывается во времени и не имеет скачков фазы. Простейший вариант схемы показан на рис.2.3. Два интерферирующих пучка обычно получают в результате деления исходного пучка с помощью полупрозрачного зеркала и направляют в область интерференции по двум разным траекториям ТР1 и ТР2.

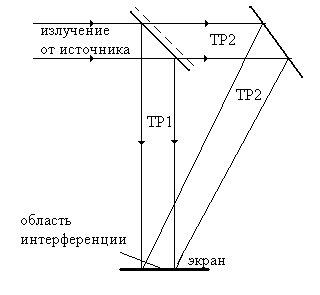
Рис.2.3 Простейшая схема получения интерференционной картины.

Разность фаз Δφ₁₂ этих двух оптических волн, прошедших по траекториям ТР1 и ТР2, зависит от разности оптических длин при прохождении волн по этим траекториям.

В том случае, если излучение не прерывается во времени и траектории не изменяются во время наблюдения, разность фаз остается постоянной, интерференционная картина остается неподвижной и не смещается относительно выбранного начального отсчета.

Однако излучение является строго непрерывным только в идеале, и можно сказать, что это некоторая теоретическая идеальная модель, недостижимая на практике. Реально излучение лазера происходит не непрерывно, а состоит из следующих друг за другом пакетов волн (или, по-другому, из цугов волн), длительность которых конечна. При этом следует заметить, что чем короче волновой пакет, тем шире спектр линии излучения, Волновые пакеты следуют один за другим. Однако следующий волновой пакет не является продолжением предыдущего, начальная фаза его колебаний не связана с предыдущим пакетом.

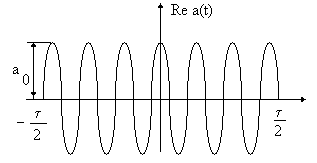
Рис.2.4 Гармонический волновой пакет.

Это означает, что на границе между пакетами происходит произвольный фазовый скачок. Другими словами (упрощенно) можно представить, что вынужденное лазерное излучение первого пакета порождается некоторым атомом А₁, а вынужденное излучение второго пакета порождается другим атомом А₂ и не связано с излучением атома А₁. . Бесконечно длинная монохроматическая волна имеет бесконечно узкий спектр частот. Реальное излучение лазера не является строго монохроматическим, а имеет конечную ширину спектра излучения.

2.3.2. Спектр волнового пакета. Рассмотрим волновой пакет гармонических колебаний с частотой f₁ и с длительностью τ (рис. 2.4) и найдем его спектр. Положим для простоты, что амплитуда колебаний в пределах пакета не изменяется.

Рассмотрим гармоническую функцию, выражающую колебания волнового пакета на отрезке от – τ/2 до + τ/2

при

при (2.22)

Далее найдем спектр функции (2.22).

(2.23)

Распределение интенсивности по частотам спектра оптического излучения найдем как квадрат модуля функции .

(2.24)

Примерный вид зависимости А²(t) изображен на рис. 2.5.

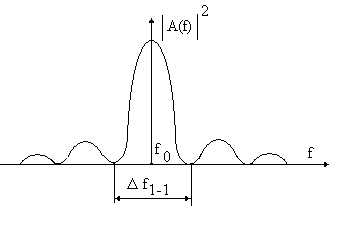
Рис.2.5. Распределение интенсивности в спектре волнового пакета.

Нули функции min (–1) и min(+1) соответствуют точкам, где . Отсюда следует, что полуширина центрального лепестка спектра частот равна .

Ширина спектральной линии по нулям равна:

(2.25)

Таким образом, ширина спектральной линии есть величина, обратная длительности волнового пакета. Протяженность волнового пакета в пространстве составляет:

, (2.26)

где с – скорость света.

Учитывая, что , выразим дифференциал Δλ через Δf.

(2.27)

(2.28)

Подставив (2.28) в (2.26), получим:

(2.29)

Выражение (2.29) определяет длину волнового пакета, которая соответствует ширине линии Δλ.

2.3.3. Длина когерентности связана с длиной волнового пакета. Если разница длин траекторий луча будет равна нулю ( ), то сложение волн, прошедших по траекториям ТР1 и ТР2 будет происходить в точном соответствии с их порядком следования: 1+1, 2+2, 3+3 и т.д. Эта ситуация иллюстрируется Рис2.5.

При этом фазы пакетов 1 и 1´, 2 и 2´, 3 и 3´ одинаковы. Разность фаз волн, приходящих на интерференционное поле, не изменяется, и, следовательно, положение интерференционной картины не меняется при последовательной интерференции различных пакетов. Видность (контрастность) усредненной во времени картины будет максимальной. Если амплитуды волн одинаковы, то коэффициент видности будет равен 1.

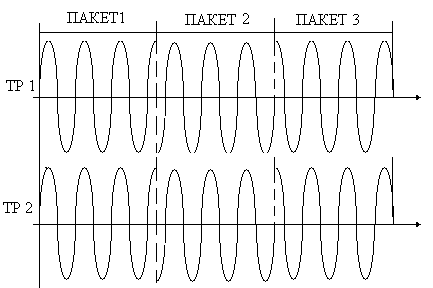
Рис.2.6.Схема наложения волновых пакетов при условии равенства длин

траекторий оптических пучков в схеме интерференции.

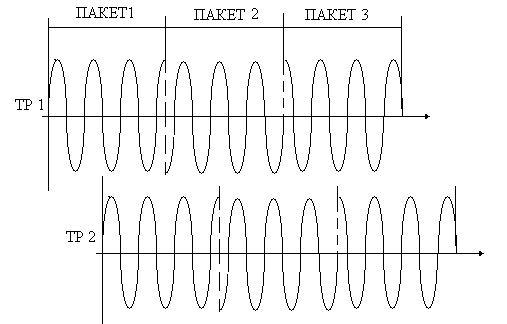
Рис.2.7. .Схема наложения волновых пакетов при условии неравенства длин

траекторий оптических пучков в схеме интерференции.

Рассмотрим случай, когда , т.е. длины траекторий Т₁ и Т₂ неодинаковы, и имеет место задержка пакетов, прошедших по траектории 2 относительно пакетов, прошедших по траектории 1. Такая ситуация показана на рис 2.7.

Пусть разность длин траекторий равна некоторой части длины волнового пакета. Тогда картина сложения волн, прошедших по траекториям ТР1 и ТР2, будет следующей : часть пакета 1 налагается на пакет 2, часть пакета 2 налагается на пакет 3 и т.д. Но в этом случае разности фаз между частями пакетов с неодинаковыми номерами будут произвольными. Положения интерференционной картины в эти промежутки времени будут произвольно изменяться во времени, то есть картина будет смещаться вдоль оси 0x при каждом скачке разности фаз между волнами. Учтем, что время наблюдения (или время экспозиции при записи на фотопленку) интерференционной картины многократно превышает длительность одного волнового пакета. Множество смещенных интерференционных картин суммируются, и в результате картина будет «смазана» и усреднена за время экспозиции. Вместо четкой интерференционной картины с высоким коэффициентом контраста мы получим некоторый более или менее равномерный серый фон, а на этом фоне интерференционную картину с низким контрастом. При уменьшении разности хода контраст (видность) интерференционной картины будет возрастать. При разнице равной половине длины волнового пакета мы получим видность интерференционной картины примерно равную половине максимальной видности, которую мы получили бы при разности хода лучей = 0. Эту величину примем за некоторую характерную длину когерентности

. (2.30)

Здесь λ_ср – средняя длина волны, соответствующая средней частоте спектральной линии, Δλ – ширина спектральной линии лазера или иного источника, соответствующая частотной ширине полосы .

Это же соотношение можно выразить в виде следующей пропорции:

, (2.31)

Это означает, что длина когерентности во столько раз больше длины волны излучения, во сколько раз длина волны больше ширины спектральной линии излучения источника на оси длин волн.