1.9 Пространственный спектр в случае дифракции оптической волны на амплитудной щелевой решетке.
Рассмотрим плоскую дифракционную решетку, образованную периодически чередующимися прозрачными и непрозрачными полосками (рис.1.16). Макет решетки такого типа легко изготовить в лаборатории путем фотографирования на фотопластинку чертежа решетки.
Рис. 1.16. Прохождение когерентного света через амплитудную щелевую решетку.
Рассмотрим решетку бесконечных размеров. Функцию пропускания в пределах периода можно описать следующим выражением:
T (x)=1 при
T
(x)=0
при
и
(1.113)
Представим функцию
пропускания в виде ряда Фурье вида
(1.94)
.
Коэффициенты
вычисляем по формулам (1.95) и (1.96) . В
результате получим:
,
(1.113)
В том случае, если ширина щели d равна половине периода решетки, коэффициенты разложения в ряд следующие:
,
,
,
,
,
….. (1.114)
Если световая
волна с амплитудой
направлена вдоль оси 0z
, т.е. по нормали к поверхности решетки,
то пространственный спектр дифрагированных
волн будет иметь вид подобный формуле
(1.100)
Коэффициенты
при этом определены выражением
(1.113).
Раздел II интерференция. Принципы интерфЕрометрии
2.1. Интерференция двух плоских волн
Рассмотрим следующую
простую задачу. На экран, расположенный
в плоскости х0у,
падают две плоские когерентные оптические
волны:
и
.
Векторы напряженности электрических
полей (векторы поляризации) этих волн
параллельны между собой и параллельны
оси 0у.
Волновые векторы
и
этих волн лежат в плоскости х0z
и направлены симметрично относительно
оси 0z
под углами +
и -
к оси 0z
(Рис 2.1).
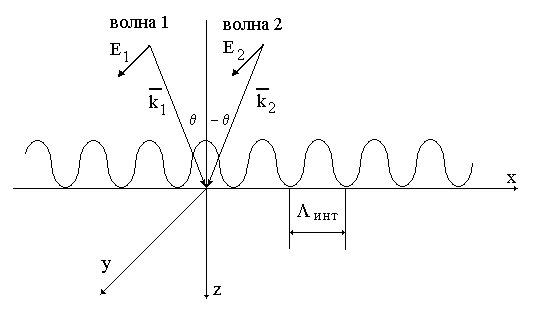
Рис 2.1. Схема ля анализа интерференции двух плоских волн.
Запишем уравнения плоских волн в виде:
.
(2.1)
Здесь
амплитуда волны;
некоторая начальная фаза,
В данном случае
проекции волновых векторов
и
на ось 0x
равны:
.
(2.2)
(2.3)
Здесь
,
пространственная частота волны по
координате 0х
,
длина волны света..
В области
интерференции, на плоскости х0у
при z
= 0, можно записать следующие выражения
для комплексных амплитуд волн
и
:
,
(2.4)
.
(2.5)
Здесь
и
некоторые начальные фазы интерферирующих
волн.
Суммарное поле волн в плоскости х0у равно:
.
(2.6)
Следует напомнить,
что при измерениях в оптике приборы
регистрируют не амплитуду волны, а ее
интенсивность, т.е. величину, пропорциональную
плотности мощности излучения. Интенсивность
определяют лак
,
и она равна произведению комплексной
амплитуды на комплексно сопряженную
величину. Найдем распределение
интенсивностей в области интерференции,
используя выражение (2.6) и формулу
.
.
(2.7)
.
(2.8)
Перемножив (2.7) и (2.8), получим:
(2.9)
Здесь
разность фаз двух когерентных волн в
точке начала координат х
= 0, z
= 0.
Анализ выражения (2.9) приводит к следующим выводам.
В области интерференции на плоскости х0у имеют место периодические изменения интенсивности с периодом интерференции
,
который можно найти из соотношения
.
Отсюда получим:
. (2.10)
Условие
соответствует расположению начала
координат
х = 0 в точке максимума распределения интенсивности интерференционной картины, наблюдаемой на плоскости х0у.
Расположим начало отсчета координаты x в максимуме интерференционной картины. Это будет соответствовать начальному сдвигу фаз
.
Если затем на пути одной из волн,
участвующих в интерференции, ввести
возмущение
показателя преломления среды,
приводящее к сдвигу фазы волны на
величину
,
то интерференционная картина сдвинется
относительно выбранной системы координат
на величину
,
которую можно определить из соотношения
,
т.е. приравняв нулю новый аргумент
косинуса. В результате находим:
. (2.11)
С учетом (2.10) соотношение (2.11) можно переписать в виде:
, (2.12)
а также выразить в виде следующей пропорции:
.
(2.13)
Итак, из выражения 2.13 следует, что дополнительный сдвиг фазы одной из интерферирующих волн вызывает сдвиг интерференционной картины, который в отношении к периоду этой интерференционной картины составляет долю, равную отношению величины дополнительного фазового сдвига, внесенного на пути оптической волны к величине 2.
Коэффициент, характеризующий видность интерференционной картины, (коэффициент контраста) обычно характеризуют следующим отношением:
.
(2.14)
В том случае, когда
амплитуды интерферирующих волн одинаковы,
этот коэффициент равен 1. Как видно из
выражения (2.9), при условии, что амплитуды
волн одинаковы, интенсивность
интерференционной картины при изменении
координаты x
изменяется в пределах от величины
до величины
.
Следует подчеркнуть, что нулевая
интенсивность в минимумах будет
наблюдаться только
в том случае,
если амплитуды когерентных интерферирующих
волн равны.
Если же амплитуды интерферирующих
волн различны, то интенсивность в
минимуме не равна нулю,
,
а видность
интерференционной
картины будет меньше единицы.
Для того чтобы убедиться в этом, проведем простой расчет. Пусть
,
(2.15)
.
Для упрощения здесь мы положили . Тогда получим:
. (2.16)
При условии, что
получим значение максимальной
интенсивности в дифракционной картине:
(2.17)
При условии, что
получим значение минимальной интенсивности
в дифракционной картине:
(2.18)
Если
,
то коэффициент видности будет меньше
1. При этом любая из этих амплитуд может
быть больше другой, это не имеет значения.
. Рассмотрим пример 1.
Пусть
,
,
тогда проведя расчет по формуле 2.16
получим:
,
,
,
Пример 2. Пусть
,
.
.
Таким образом, видность интерференционной картины снижается при увеличении разницы между амплитудами интерферирующих волн.