3.5.1. Схема пространственной фильтрации волнового фронта с целью удаления оптических шумов, рис 3.5

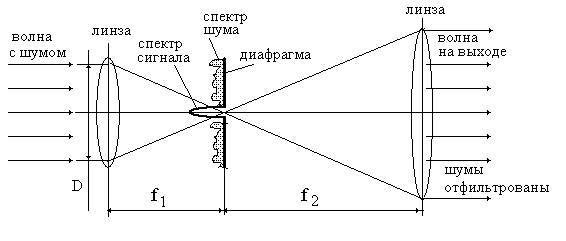
Рис.3.5. Схема пространственной фильтрации волнового фронта с применением круглой диафрагмы.

Положим, что идеальная исходная волна имеет плоский волновой фронт, однако, вследствие рассеяния на пылинках и неоднородностях предыдущих оптических элементов на плоском волновом фронте присутствуют случайные флуктуации амплитуды и фазы волны. Пространственный спектр флуктуаций обычно имеет большую ширину и расположен во всей частотной области от низких до высоких пространственных частот.

Пространственный спектр плоской волны, прошедшей через круглую апертуру с диаметром D представляет собой узкий пик диаметром главного максимума, равным:

. (3.34)

Здесь -это диаметр главного максимума распределения мощности излучения в фокальном пятне линзы (диаметр первого темного кольца в пятне Эйри), измеренный по нулевому уровню распределения мощности в фокальном пятне. Распределение интенсивности в пятне Эйри выражается через функцию Бесселя: , где r- радиальная координата, a- радиус круглой апертуры, k- волновое число, интенсивность в центре пятна Эйри. При этом доля мощности излучения, сосредоточенной в пределах главного максимума пятна Эйри т.е. внутри первого темного кольца, составляет более 80% , а доля мощности излучения внутри второго темного кольца составляет более 90% полной мощности излучения. , [М. Борн, Э. Вольф. Основы оптики. М. Наука 1970г. Глава 8 , с.434]

Если диаметр диафрагмы равен или несколько больше диаметра , то основная доля мощности плоской волны пройдет через диафрагму и после прохождения через вторую линзу волна преобразуется в волну с волновым фронтом, с формой, близкой к плоской. При этом волновой фронт очищен от оптических шумов, так как спектральные составляющие шумов практически не проходят через диафрагму.

Пример расчета. Дано: диаметр пучка D=1мм., фокусное расстояние линзы =20мм. Рассчитаем диаметр центрального пятна при =0,6мкм.

На практике сложно изготовить подобную диафрагму установить ее с точностью порядка единиц микрометров. Поэтому на практике следует взять диафрагму с диаметром в 2-3 раза больше расчетного диаметра центрального пятна. При этом резко снижаются требования к точности установки диафрагмы, и несколько увеличивается доля мощности основного излучения. Вместе с тем, интегральная мощность шумов также увеличивается пропорционально площади отверстия.

3.5.2. Пространственная фильтрация с применением фазового фильтра. Метод фазового контраста.

В ряде случаев представляет интерес наблюдение и исследование фазовых объектов, у которых полезная информация заключена в пространственной фазовой модуляции транспаранта. Фазовая пространственная модуляция неразличима глазом при простом непосредственном наблюдении. Метод фазового контраста позволяет преобразовать фазовую модуляцию в амплитудную, которую легко можно наблюдать визуально. Оптическая схема, реализующая метод фазового контраста изображена на рис. 3.6. Рис.3.6. Схема пространственной фильтрации по методу фазового контраста.

Фазовый транспарант можно описать функцией вида:

(3.35)

Будем рассматривать эту задачу в приближении малой глубины фазовой модуляции, при этом можно записать: . С помощью первой линзы в оптической схеме выполняется преобразование Фурье при переходе из плоскости первой линзы к ее фокальной плоскости. Преобразование Фурье функции будет иметь вид:

(3.36)

Здесь функция является Фурье преобразованием функции модуляции . В плоскости пространственных частот эта функция распределена в широком диапазоне координат этой плоскости. В то же время функция сосредоточена в области нулевых координат фокальной плоскости.

Пространственный фильтр представляет собой прозрачную пластинку, в центральной части которой создано утолщение (а возможно и углубление), которое создает дополнительный фазовый сдвиг проходящей оптической волны на по отношению ко всей остальной пластине. Напомним, что .Если отбросить постоянный фазовый сдвиг в прозрачной пластине, то воздействие фильтра на волну в фокальной плоскости будет выражаться следующими операциями. В выражении (3.36) первое слагаемое следует умножить на ,

а второе слагаемое следует умножить на 1. В результате выражение, описывающее пространственный спектр на выходе фильтра примет вид:

(3.37)

Вторая линза выполняет обратное Фурье преобразование. В результате на выходе мы получаем следующее распределение:

(3.38)

Отбросив постоянный фазовый сдвиг на 90 градусов (т.е. ) на всей плоскости, мы видим, что функция представляет собой амплитудную модуляцию. В этом можно убедиться также, если найти распределение интенсивности, помножив выражение (3.38) на комплексно сопряженное выражение.

(3.39)

В результате мы показали, что рассмотренная здесь оптическая схема преобразует фазовую модуляцию в амплитудную. Схему можно применить для наблюдения и исследования фазовых, например биологических объектов.